Вариант № 24

1. Вычислить интегралы

1.1

1.2

2. найти площадь фигуры, ограниченной линиями:

.

3. Вычислить площадь поверхности, образованной вращением плоской фигуры (ограниченной данными линиями) вокруг указанной оси: вокруг оси Ох.

4. Вычислить несобственный интеграл или показать, что он расходится

6.1 ;

6.2 .

5. вычислить работу, необходимую для выкачивания нефти плотностью ρ= 0.8·10^-3 кг/м³ из вертикального цилиндрического резервуара радиусом основания R, высотой Н. Принять R= 3 м, Н = 4 м.

6. по закону Паскаля сила Р, с которой жидкость плотности ρ давит на площадку S при глубине погружения Н равна Р = ρgНS. Найти силу давления жидкости удельного веса δ на вертикальный эллипс с осями 2а и 2b, центр которого погружен в жидкость на глубину h (h≥ b), причем большая ось эллипса параллельна уровню жидкости.

Вариант № 25

1. вычислить интегралы

1.1

1.2

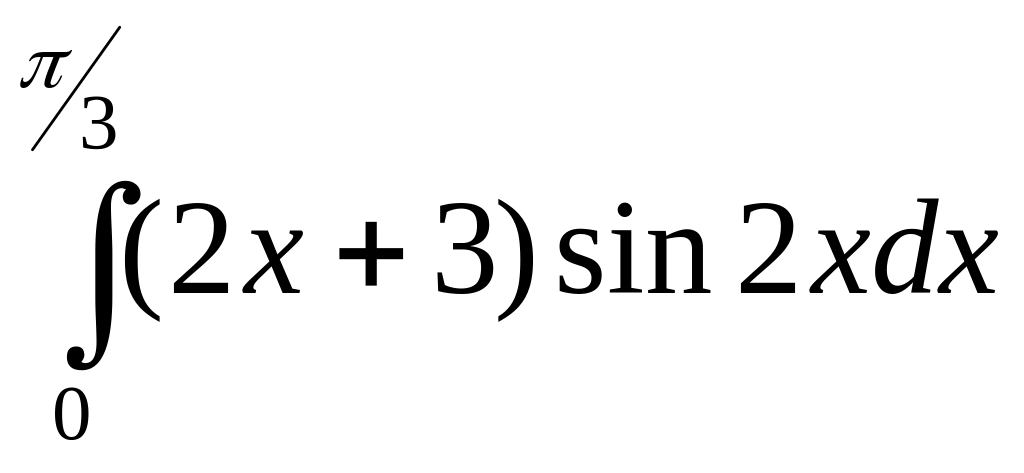
2. найти площадь фигуры, ограниченной данными линиями

.

3. определить объем тела, образованного вращением плоской фигуры (ограниченной данными линиями) вокруг указанной оси: 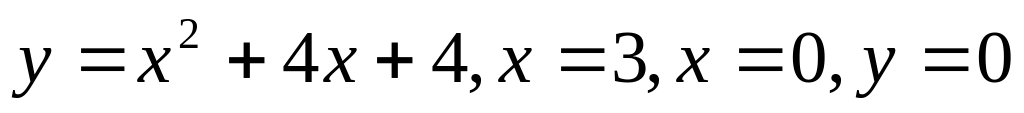вокруг оси Ох.

4. вычислить несобственный интеграл или показать, что он расходится

   6.1 ;

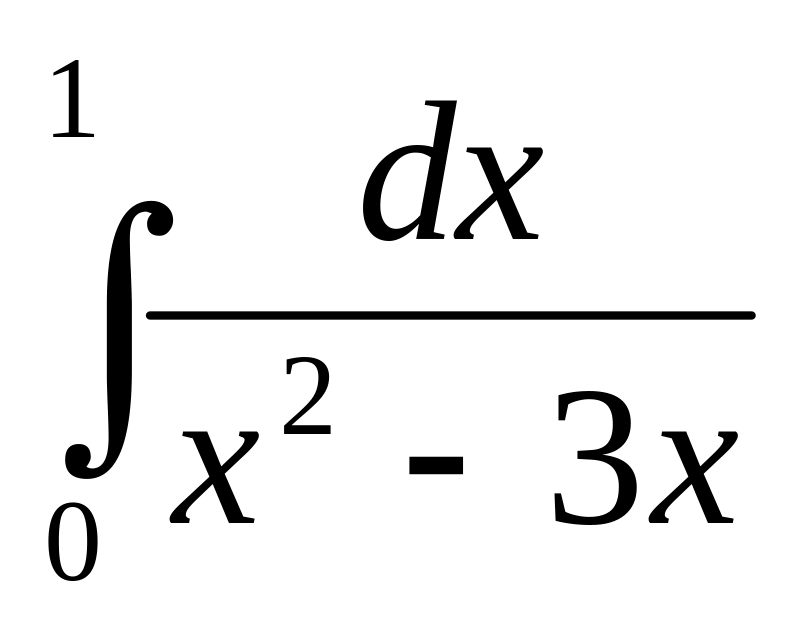   6.2 .

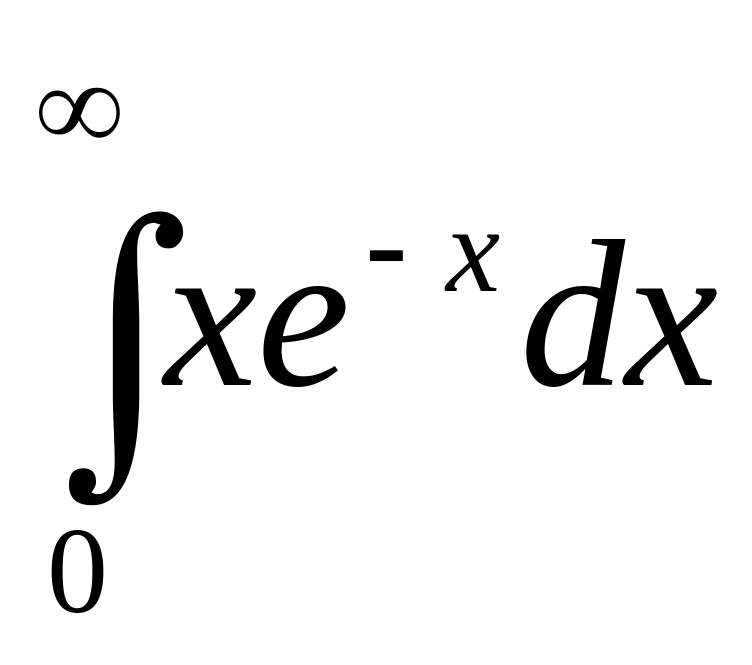5. вычислить работу, которую нужно затратить, чтобы выкачать жидкость удельного веса δ, заполняющую полусферический резервуар радиуса R. Принять R= 4 м.

6. по закону Паскаля сила Р, с которой жидкость плотности ρ давит на площадку S при глубине погружения Н равна Р= ρgНS. С какой силой жидкость плотности ρ давит на вертикальную треугольную пластину с основанием a и высотой h, погруженную в жидкость вершиной вниз так, что основание треугольника находится на ее поверхности.