12. Закон Малюса

Закон Малюса – зависимость интенсивности линейно-поляризованного света после его прохождения через анализатор от угла φ между плоскостями поляризации падающего света и анализатора. 

Установлен Э. Л. Малюсом в 1810 г. Если I₀ и I – соответственно интенсивности падающего на анализатор и выходящего из него света, то, согласно закону Малюса, I = I₀cos²φ. Свет с иной (не линейной) поляризацией может быть представлен в виде суммы двух линейно-поляризованных составляющих, к каждой из которых применим закон Малюса. 

Поставим на пути естественного света два поляроида, оси пропускания которых развернуты друг относительно друга на угол φ (рис.1).

Вектор E_I световой волны после первого поляроида будет параллелен PP. Этот поляроид называют поляризатором, т.к. после него естественный свет стал поляризованным.

После второго поляроида останется лишь вектор E_II, параллельный P'P' его оси пропускания:

E_II  = E_I cosφ.

Т.к. интенсивность света  I ~ E², то, после второго поляроида интенсивность будет

I = I_I cos²φ

где I_I – интенсивность перед вторым поляроидом. Полученное соотношение между интенсивностями носит название закона Малюса.

Если I_I выразить через I₀, то закон Малюса примет вид:

I = ½ I_o•cos²φ

Малюса закон

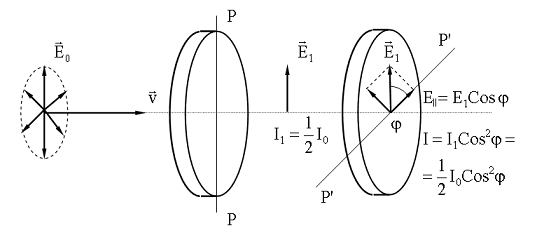
Рис.1

13. Закон Брюстера. Степень поляризации

Пусть угол падения i таков, что отраженный луч перпендикулярен преломленному, т.е. r = π/2 - i_Бр. Это условие называют условием Брюстера (см. рисунок ниже), а угол - углом Брюстера - i_Бр.

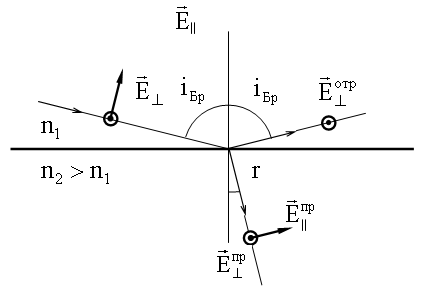
Используя закон преломления

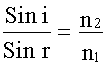(17.1.3.),

получим формулу, определяющую угол Брюстера:

.

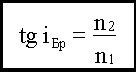При выполнении условия Брюстера i + r = π/2, тогда из формулы Френеля для   получим:

Таким образом, при выполнении условия Брюстера, отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения.

Выражение

называется степенью поляризации. Для плоскополяризованного света I_min=0 и Р=1; для естественного света I_max=I_min и P=0. К эллиптически- поляризованному свету  понятие степени поляризации не применимо  (у такого света колебания  полностью упорядочены, так что степень поляризации всегда равна 1).

16. Дисперсия света

Диспе́рсия све́та (разложение света) — это явление зависимости абсолютного показателя преломления вещества от длины волны света.

Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму(опыт Ньютона). Причиной дисперсии является неодинаковая скорость распространения лучей света c различнойдлиной волны в оптической среде. Чем больше частота волны, тем больше показатель преломления и меньше ее скорость света в среде:

у красного цвета максимальная скорость в среде и минимальная степень преломления;

у фиолетового цвета минимальная скорость света в среде и максимальная степень преломления;

в вакууме скорости света разного цвета одинаковы.

Однако в некоторых веществах (например в парах йода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают.

Дисперсия белого света указывает на его составную природу.

Белый свет разлагается на спектр и в результате прохождения через дифракционную решётку. Причем дифракционный и призматический спектры несколько отличаются: Призматический спектр сжат в красной части и растянут в фиолетовой (располагается в порядке убывания длины волны: от красного к фиолетовому). Нормальный (дифракционный) спектр равномерный во всех областях (располагается в порядке возрастания длин волн: от фиолетового к красному).

Дисперсия света дала своё название закону дисперсии, связывающему частоту и волновое число любого колебательного процесса, не обязательноэлектромагнитной волны.

Дисперсией объясняется факт появления радуги после дождя. Дисперсия является причиной хроматической аберрации — одного из тщательно устраняемых недостатков (аберраций) оптических систем, в том числе фотографических и видео-объективов.

Коши пришел к формуле, выражающей зависимость показателя преломления от длины волны n = a + b / L² + c / L⁴ + ...

,где L - длина волны в вакууме, a,b,c, ... - постоянные, значения которых для каждого вещества должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши.

Благодаря дисперсии света, можно наблюдать цветовую "игру" на гранях бриллианта.