9. Критерий Рэлея

Одной из основных характеристик спектрального прибора (будь то дифракционная решётка или призма) является его разрешающая сила. Разрешающая сила спектрального прибора определяется безразмерной величиной

                        (9.12)

Здесь: δλ — минимальная разность длин волн двух спектральных линий, при которой спектральный аппарат разрешает эти линии, т.е. позволяет их рассмотреть на экране наблюдения раздельно.

Выясним, от чего зависит разрешающая сила дифракционной решётки.

Согласно критерию Рэлея спектральные линии с длинами волн λ₁ и λ₂ = λ₁+ δλ будут разрешены, если главный максимум для одной длины волны совпадает с первым дифракционным минимумом в том же порядке для другой длины волны (рис. 9.5.б).

                                   

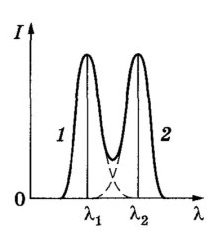
                                                      Рис. 9.5                           

Условие m-го максимума для волны λ₂ = λ₁ + δλ:

d sin φ_max = m (λ + δλ)                 (9.13)

Условие первого минимума, ограничивающего m-ый максимум волны λ:

                   (9.14)

В случае минимальной разности длин волн δλ, условия (9.13) и (9.14) описывают одну и ту же точку экрана, т.е. d sin φ_max = d sin φ_{min .}

Иными словами, условие Рэлея позволяет записать следующее равенство:

         или       

Отсюда следует, что разрешающая сила дифракционной решётки зависит только от числа её щелей (N) и от номера (m) спектра, в котором разрешаются спектральные линии.

                             (9.15)

10. Угловая и линейная дисперсия

Угловая дисперсия дифракционной решетки:

 ,

где δ. - угловое расстояние между двумя спектральными

линиями с разностью длин волн δλ,   - угол дифракции, k=1,2,3...

Выразим угловую дисперсию через постоянную решетки d, порядок спектра m и угол φ, под которым наблюдается максимум. Для этого найдем дифференциал от правой и левой части условия главного максимума (19.4.1):

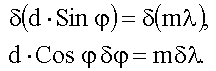
• Линейная дисперсия дифракционной решетки:

,

где l - расстояние вдоль экрана наблюдения,  δl - линейное расстояние между двумя спектральными

линиями с разностью длин волн δλ.

При наблюдении дифракции с помощью собирающей линзы при малых углах (φ << 1) из рисунка, приведенного ниже, можно найти связь линейной и угловой дисперсии:

,

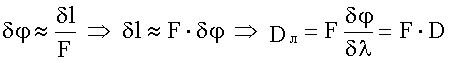
Если наблюдение дифракционной картины ведется без линзы, на большом расстоянии L от решетки, то тогда при малых углах

.

11. Поляризация электромагнитных волн. Линейная, круговая и эллиптическая поляризация

Поляризация электромагнитных волн (ПЭВ) — одно из фундаментальных свойств оптического излучения (света), состоящее в искажении различных направлений в плоскости, перпендикулярной световому лучу (направлению распространения световой волны).

ПЭВ — явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H.

Когерентное электромагнитное излучение может иметь:

Линейную поляризацию — в направлении, перпендикулярном направлению распространения волны;

Круговую поляризацию — правую либо левую, в зависимости от направления вращения вектора индукции;

Эллиптическую поляризацию — случай, промежуточный между круговой и линейными поляризациями.

Некогерентное излучение может не быть поляризованным, может быть полностью или частично поляризованным любым из указанных способов. В таком случае понятие поляризации понимается статистически.

При теоретическом рассмотрении поляризации волна полагается распространяющейся горизонтально. В этом случае можно рассматривать вертикальную и горизонтальную линейные поляризации волны.

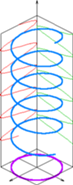
Линейная поляризация Круговая поляризация Эллиптическая поляризация