Математические методы

11. Линейное программирование. Целевая функция и ограничения.

12. Формализация структуры сети. Графы. Матрицы смежности и инциденций.

13. Алгоритм определения связности графа.

14. Алгоритм нахождения кратчайшего пути в графе.

15. Марковские цепи. Матрица переходных вероятностей и ее применение. Стационарное распределение вероятностей состояний.

16. Марковские случайные процессы. Потоки событий. Простейший поток и его свойства.

17. Процессы размножения и гибели. Уравнения Колмогорова. Стационарное распределение вероятностей состояний.

18. Системы массового обслуживания. Характеристики СМО.

Информационная безопасность

19. Шифрация сообщений методом псевдослучайных последовательностей. Синтез ПСП.

20. Шифрация сообщений методом псевдослучайной перестановки. Синтез псевдослучайных перестановок.

21. Виды модуляции сигналов, используемых для передачи цифровых сообщений.

22. Помехозащищенные коды. Их характеристики. Способы описания процедуры кодирования в матричном виде.

23. Помехозащищенные коды. Их характеристики. Способы описания процедуры кодирования в полиномиальном виде.

Архитектура эвм.

24. Аналоговый и цифровой сигнал.

25. Структурная схема ПК.

26. Назначение аппаратных прерываний.

27. Организация памяти в ПК.

28. Параллельная и последовательная передача данных.

29. Назначение общей шины.

30. Назначение таблицы векторов прерываний.

31. Логическое распределение памяти.

Литература

1. Подбельский В.В. Язык Си++ – М.: Финансы и статистика, 2007.

2. Семакин И.Г., Шестаков А.П. Основы программирования – М.:Мастерство, 2010.

3. Березин Б.И., Берзин С.Б. Начальный курс Си++. – М.: Диалог-МИФИ, 2008.

4. Павловская Т.А., Щупак Ю.А. С/С++. Структурное программирование. Практикум.– СПб.: ПИТЕР, 2007.

5. Павловская Т.А., Щупак Ю.А. С/С++. Объектно – ориентированное программирование. Практикум.– СПб.: ПИТЕР, 2007.

ПРИЛОЖЕНИЕ 2

ПЕРЕЧЕНЬ ЗАДАНИЙ НА ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ

И ПРОФЕССИОНАЛЬНАХ ЗАДАЧ

Математические методы и Численные методы

1. Отделить аналитически корни уравнения

Разработать блок- схему алгоритма решения уравнения методом хорд и выбрать

точку начального приближения.

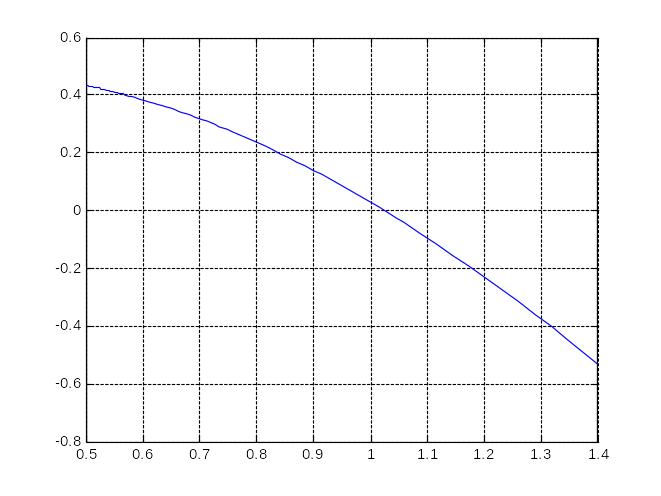
2. Корень уравнения F(x)=0, где F(x)=tg(0.4x+0.4)-x² отделен на интервале

[0.5; 1.4] ] .Заданы m1=min(F’(x)) и M2=max(F”(x)) на указанном интервале.

Обосновать выбор точки начального приближения для уточнения корня

уравнения методом Ньютона с заданной точностью ε и разработать блок – схему

алгоритма.

График функции

3. В ычислить

методом прямоугольников, программно реализовав последний в MatLab.

Сравнить полученное значение с результатом, полученным интегрированием в аналитическом виде. Вычислить величину погрешности вычисления, как модуль разности между численным и аналитическим результатами.

F(x)=e^x + 18x² +x ; a=0;b=5; Количество участков разбиения N=100.

4 . Разработать вычислительный алгоритм с минимальным числом умножений для вычисления функции путем разложения в ряд Тейлора с заданной точностью ε. Алгоритм программно реализовать на MatLab.

5. В MatLab задать вектор-столбец размерностью 10 и вычислить sin от его компонент.

6. С помощью MatLab вывести график функции F(x)= tg(0.5x+0.2)-x² на интервале

[0.3; 1.0] .

7. С помощью MatLab построить в одном окне графики двух функций

у= ;

8. С помощью MatLab продифференцировать в символьном виде функцию

у=

9.Задана таблица сообщений и их частостей появления в тексте.

А	B	C	D	E
50	30	10	5	5

Закодировать сообщения кодом Хаффмана.

10. Использовать MatLab для численного решения системы линейных уравнений. Матрица системы и вектор-столбец правых частей уравнений задать самостоятельно. Полученное решение подставить в систему с целью контроля правильности.

10. Вычислить в MatLab среднее арифметическое компонент вектора.