2. Synthesis of Synchronous fsm

Types of Tasks

Task 2.1

Design a circuit of a detector of input sequence specified by the variant of a task.

At giving the sequence to the input of Mealy FSM, signal "1" appears in its output. In all other cases - signal "0".

The variants of the tasks are presented in Table 6.

Table 6

Number of variant	Input sequence
1.	11011, 10011
2.	10001, 11001
3.	010101, 000101
4.	10010, 10011
5.	001010, 101010
6.	111011, 111010
7.	000110, 100110
8	1110001, 101011
9	101011, 1110011
10	100001, 010111

Task 2.2

Design an FSM circuit, the input alphabet of which X = {A, B, C}, output alphabet of which {0,1,2}. FSM distinguishes input words and forms output words according to variant of the task presented in Table 7.

Table 7

Variant	Input words
1.	ABCC – 1, BCAA – 2
2.	ABBA – 1, ACBA – 2
3.	CBAA – 1, CABCA – 2
4.	ABCA – 1, CABC– 2
5.	CCBAA – 1, CAB – 2
6.	BBCA – 1, BAAC – 2
7.	ABACB – 1, CAB – 2
8.	CCAB – 1, AABC – 2
9.	AAAB – 1, BCAB -2
10.	AABBC – 1, BCC -2
11.	ABAAA -1, BACB – 2
12.	BBBC -1, ABC – 2
13.	CCBC – 1, CCAB -2
14.	ABBCA -1, BBA – 2
15.	BCABC -1, CB – 2
16.	BABC – 1, CAAC – 2
17.	AABA – 1, CBCB – 2
18.	CBAB – 1, BACB – 2
19.	AABA – 1, BBA – 2
20.	CCBC -1, AAB -2
21.	AABC -1, BCAC – 2
22.	ABCAB -1, CA -2
23.	AACAB – 1, BBA -2
24.	BBAB -1, CBA – 2
25.	ACBA – 1, CBAAB -2
26	AABCC – 1, ABAB – 2
27	CBACB – 1, AABAB – 2
28	ACCBA – 1, ACCC- 2
29	BBCCA – 1, CBCA – 2
30	AABBC – 1, CCBCA – 2

Task 2.3.

Design Mealy FSM circuit, controlled by code lock, with one input X and two outputs Y₁, Y₂.

The output signal Y₁ equals 1 in case X = 0, and the previous 5 steps in input X sequence, given by Table 10, from units and zero entered.

The output signal Y₂ should equal 1 only when the current value X is correct from the viewpoint of FSM progress to the side of state at which the code lock is open.

The task variants are presented in Table 8.

Table 8

Number of variant	Input sequence
1.	11011
2.	01010
3.	10101
4.	00011
5.	10011
6.	10110
7.	01001
8.	11001
9.	00100
10.	01100

Task 2. 4.

Design a circuit of binary-coded decimal synchronous counter for different variants of coding decimal numbers. The counter accepts states from 0 to 9.

Table 10

Number of variant	Binary-decimal code	Counter direction
1.	Code with excess3	Up
2.	Code with excess 3	Down
3.	Code 2 out of 5	Up
4.	Code 2 out of 5	Down
5.	Biquinary code	Up
6.	Biquinary code	Down
	Codes with weights
7.	2 4 2 1	Up
8.	2 4 2 1	Down
9.	6 4 2 -1	Up
10.	6 4 2 -1	Down

Task 2. 5.

Design Moore FSM circuit, the sequence of state changes of which is presented in Table 11.

In column “Output signal”, states are listed, in which the output of FSM is equal to one, in all other cases – “0”.

Table 11

Number of variant	Sequence of states	Output signal
1.	IN=1. 0®1®3®5®4®0 … IN=0. 0®5®4®3®1®0 …	1 , 5
2.	IN=1. 0®2®7®1®4®0 … IN=0. 0®1®4®7®2®0 …	2,7
3.	IN=1. 0®5®2®1®3®0 … IN=0. 0®3®5®1®2®0 …	1,2,5
4.	IN=1. 0®3®6®5®2®0 … IN=0. 0®6®2®3®5®0 …	3,5
5.	IN=1. 0®1®6®2®5®0 … IN=0. 0®5®6®1®2®0 …	2,6
6.	IN=1. 0®5®4®1®3®0 … IN=0. 0®3®5®1®4®0 …	1,3
7.	IN=1. 0®2®1®7®6®0 … IN=0. 0®1®6®7®2®0 …	2,7
8.	IN=1. 0®2®7®1®4®0 … IN=0. 0®1®4®7®2®0 …	1,4

Sequence of FSM synthesis

1. According to the given description, design a transition graph of FSM.

2. Choose the type of a flip-flop on which the FSM is implemented.

3. Assign FSM states.

4. Define excitation and output functions of FSM.

5. Minimize the obtained logic functions.

6. Design a circuit of FSM in AND, OR, NOT base.

7. Describe FSM in Verilog.

8. Simulate using VCS.

9. Synthesize the circuit with the help of Design Compiler. Use SAED EDK32/28nm technology library.

10. Specification using digital cells of SAED EDK90nm library.

Example (Part 1)

Design a circuit of the device that performs the conversion of input binary decimal code into output binary decimal code.

The weights of input code – 2421, the weight of output code – 8421.

The circuit of the code convertor has four inputs and four outputs.

1. Composition of the table of input and output codes.

Input and output codes are defined in the following way:

X = x₁p₁ + x₂p₂ +x₃p₃ + x₄p₄ = x₁2 + x₂4 +x₃2 + x₄1,

Y = y₁p₁’+y₂p₂’+y₃p₃’+y₄p₄’= y₁8+y₂4+y₃2+y₄1, where x_i,y_i{0,1}.

Table 12

Decimal digit	Input code	Output Code
0	0 0 0 0	0 0 0 0
1	0 0 0 1	0 0 0 1
2	0 0 1 0	0 0 1 0
3	0 0 1 1	0 0 1 1
4	0 1 0 0	0 1 0 0
5	1 0 1 1	0 1 0 1
6	1 1 0 0	0 1 1 0
7	1 1 0 1	0 1 1 1
8	1 1 1 0	1 0 0 0
9	1 1 1 1	1 0 0 1

2. Composition of the table of implementing functions

Table 13

x1 x2 x3 x4	y1 y2 y3 y4
0 0 0 0	0 0 0 0
0 0 0 1	0 0 0 1
0 0 1 0	0 0 1 0
0 0 1 1	0 0 1 1
0 1 0 0	0 1 0 0
0 1 0 1	x x x x
0 1 1 0	x x x x
0 1 1 1	x x x x
1 0 0 0	x x x x
1 0 0 1	x x x x
1 0 1 0	x x x x
1 0 1 1	0 1 0 1
1 1 0 0	0 1 1 0
1 1 0 1	0 1 1 1
1 1 1 0	1 0 0 0
1 1 1 1	1 0 0 1

Boolean Functions Minimization

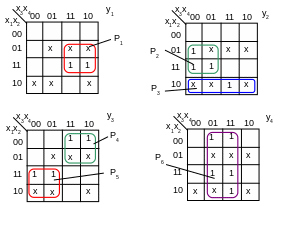
Fig.5. Minimization of functions using Karnaugh maps

y₁= x₂x₃; y₂=x₂ ~x₃ +x₁~x₂; y₃ =~x₁x₃+x₁~x₃; y₄=x₄;

3. Design of circuits of the device on AND, OR, NOT basis

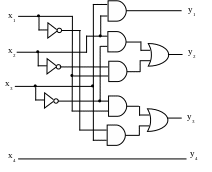
Fig. 6. The circuit using AND, OR, NOT gates

4. Design of circuits of the device on NAND basis

y ₁= x₂x₃; y₂=(x₂ ~x₃)(x₁~x₂); y₃ =(~x₁x₃ )(x₁~x₃) ;

Fig. 7. The circuit using NAND gates

5. Design of circuits of the device in basis NOR

y ₁ = x₂x₃ = x₂ +x₃

P₁₀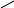

To obtain y₂ and y₃ in POS it is possible to use Karnaugh maps for inverse functions y₂,y₃.

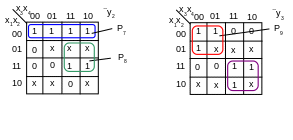
Fig. 8. Karnaugh maps for inverse functions

y₂ = x₁x₂ + x₂x₃;

y₂ = x₁x₂ + x₂x₃ = (x₁+x₂) + (x₂ +x₃) ;

y₃ = x₁x₃ + x₁x₃;

y₃ = x₁x₃ + x₁x₃ = (x₁+x₃) + (x₁ +x₃) ;

y₄ = x₄;

Fig. 9. The circuit using NOR gates

6. Definition of polynomials of implementing functions.

The polynomial form f(x₁,x₂,x₃,x₄) in general case:

f(x₁,x₂,x₃,x₄) = c₀  c₁x₁  c₂x₂  c₃x₃ c₄x₄  c₁₂x₁x₂  c_­13x₁x₃  . . .  c₁₂₃₄ x₁x₂x₃x₄,

where c_i{0,1}.

Find polynomial forms of y₁,y₂,y₃,y₄ functions, proceed from minimized form of these functions.

y₁ = x₂x₃;

y₂=x₂ x₃ +x₁x₂

Replace operation + by .

Then y₂=x₂ (1 x₃) +x₁ (1 x₂) = x₁  x₂  x₁x₂  x₂x₃;

y₃ = x₁x₃+x₁x₃ = x₁  x₃

y₄=x₄;

7. Implementation of the circuit of the code converter on the decoder

Decoder 4×16 is used to implement a function of 4 variables. But y₁,y₂,y₃ depend on three variables only, therefore decoder 3×8 can be used.

Table 13

x1 x2 x3	y1 y2 y3
0 0 0	0 0 0
0 0 1	0 0 1
0 1 0	0 1 0
0 1 1	x x x
1 0 0	x x x
1 0 1	0 1 0
1 1 0	0 1 1
1 1 1	1 0 0

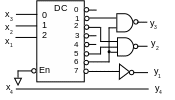
Fig.10. The circuit realization using decoder

8. Implementation of the circuit of the code converter on multiplexers

Multiplexers 4 – 1 are used to implement functions y₁,y₂,y₃.

Y = I₀S₁S₀ +I₁S₁S₀ + I₂S₁S₀ + I₃S₁S₀

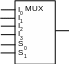
Fig. 11. Logic symbol for multiplexer

• y₁ implementation

y1 = x₂x₃;

x₂, x₃ are entered to S₁ and S₀ inputs. Shannon cofactors y₁ by x₂,~x₂, x₃, ~x₃ are entered to inputs I₀, I₁, I₂, I₃ .

I₀= y1_~x2,~x3 = 0;

I₁ = y1_~x2,x1 = 0;

I₂ = y1_x2,~x1 = 0;

I₃ = y1_x2,x1 = 1;

• y₂ implementation

x₂, x₃ are entered to S₁ and S₀ inputs. Shannon cofactors y₂ by (~x3,~x2) – y2_~x3,~x2 is entered to I0 input, cofactor y2_­~x3,x2 are given to I1 input, cofactor y2_x3,~x2 are given to I2 input , cofactor y2_x3,x2 are given to I₃ input.

y2 = x₂ ~x₃ +x₁~x₂;

I₀ = y2_~x2,~x3 = x₁;

I₁ = y2_~x2,x3 = x₁;

I₂ = y2_x2,~x3 = 1;

I₃ = y2_x2,x3 = 0;

• y₃ implementation

x₁,x₃ are entered to S₁ and S₀ inputs. Shannon cofactors y3 by x1,~x1, x3, ~x3 are entered to inputs I₀, I₁, I₂, I₃ .

y3 =~x₁x₃+x₁~x₃;

I₀ = y3_~x1,~x3 = 0;

I₁ = y3_~x1,x3 = 1;

I₂ = y3_x1,~x3 = 1;

I₃ = y3_x1,x3 = 0;

The circuit is presented at Fig.9.

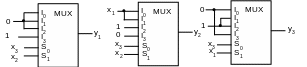
Fig.12. The circuit realization using multiplexers

9. Gate level description of the code converter circuit

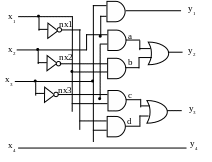
Fig.13. The circuit using AND, OR, NOT gates

module converter_decimal_numbers (x1,x2,x3,x4,y1,y2,y3,y4);

// port declarations

input x1,x2,x3,x4;

output y1,y2,y3,y4;

// internal wire declarations

wire nx1,nx2,nx3, a,b,c,d;

// create nx1,nx2,nx3;

not (nx1,x1);

not (nx2,x2);

not (nx3,x3);

// and gates instantiations

and (y1,x2,x3);

and (a,x2,nx3);

and (b,nx2,x1);

and (c,nx3,x1);

and (y1,nx1,x3);

//or gates instantiations

or (y2,a,b);

or (y3, c,d);

buf (y4,x4);

endmodule

Behavior Description of the code converter circuit

module converter_decimal_numbers (x,y);

input[1:4] x;

output reg [1:4] y;

always@(x)

case (x)

0: y=4b’0000;

1: y=4b’0001;

2: y=4b’0010;

3: y=4b’0011;

4: y=4b’0100;

5,6,7,8,9,1,10: y=4b’xxxx;

11: y=4b’0101;

12: y=4b’0110;

13: y=4b’0111;

14: y=4b’1000;

15: y=4b’1001;

endcase

endmodule

Synchronous FSM Synthesis (Part II)

Example

Design an FSM circuit, the input alphabet of which X = {A, B, C}, output alphabet of which {0,1,2}. FSM detects input words and forms output symbols in the following way:

If input word is BBCAB, Y=1.

If input word is BBC, Y=2. In all other cases Y=0.

1. Composition of Mealy FSM graph

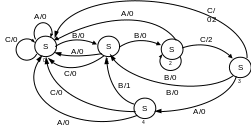
Fig. 14. State diagram of Mealy FSM

2. State minimization

Minimization task is in partitioning of set of states into classes of equivalent states and exchange of each class by one state.

1 = {X1,Y1,Z1}; X1={S₀,S₁,S₃}; Y1={S₂}; Z1={S₄}

Si X	A	B	C	
S0	S0/0	S1/0	S0/0	X1
S1	S0/0	S2/0	S0/0	X1
S2	S0/0	S2/0	S3/2	Y1
S3	S4/0	S1/0	S0/0	X1
S4	S0/0	S1/1	S0/0	Z1

Si X	A	B	C	
S0	X1	X1	X1	X2
S1	X1	Y1	X1	Y2
S2	Z1	X1	X1	Z2
S3	-	-	-	W2
S4	-	-	-	K2

2 = {X2,Y2,Z2,W2,K2};

Each class contains only one state. Therefore FSM has no equivalent states.

The structure of Mealy FSM

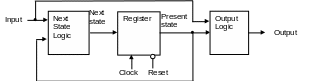
Fig. 15. Clocked synchronous Mealy FSM structure

3. Input and output signals coding

• Coding input symbols

Input	x1 x2
A	0 0
B	0 1
C	1 0

• Coding output symbols

Output	y1 y
“0”	0 0
“1”	0 1
“2”	1 0

4. State assignment

Determine the number of state variables: choose the minimal number of state variables

n= log₂ S where S – the number of states.

n=3.

The memory of FSM (register) is implemented using rising edge triggered JK flip-flops with asynchronous reset.

Symbols q1,q2,q3, are used for the present state variables.

The choice of state assignment is arbitrary in considering example.

State	q1 q2 q3
S0	0 0 0
S1	0 0 1
S2	0 1 0
S3	0 1 1
S4	1 0 0

JK flip-flop excitation functions matrix

Transition	J K
0 - 0	0 x
0 - 1	1 x
1 - 0	x 1
1 - 1	x 0

5. Structural Table of Transitions

Present State q1 q2 q3		Input x1 x2	Next State q1 q2 q3	Output y1 y2	Excitation Functions J1 K1 J2 K2 J3 K3
S0	0 0 0	0 0	S0 0 0 0	0 0	0 x 0 x 0 x
		0 1	S1 0 0 1	0 0	0 x 0 x 1 x
		1 0	S0 0 0 0	0 0	0 x 0 x 0 x
S1	0 0 1	0 0	S0 0 0 0	0 0	0 x 0 x x 1
		0 1	S2 0 1 0	0 0	0 x 1 x x 0
		1 0	S0 0 0 0	0 0	0 x 0 x x 1
S2	0 1 0	0 0	S0 0 0 0	0 0	0 x x 1 0 x
		0 1	S2 0 1 0	0 0	0 x x 0 0 x
		1 0	S3 0 1 1	1 0	0 x x 0 1 x
S3	0 1 1	0 0	S4 1 0 0	0 0	1 x x 1 x 1
		0 1	S1 0 0 1	0 0	0 x x 1 x 0
		1 0	S0 0 0 0	0 0	0 x x 1 x 1
S4	1 0 0	0 0	S0 0 0 0	0 0	x 1 0 x 0 x
		0 1	S1 0 0 1	0 1	x 1 0 x 1 x
		1 0	S0 0 0 0	0 0	x 1 0 x 0 x