
- •3. Интегральное исчисление функций одной переменной
- •3.1. Неопределенный интеграл
- •3.1.2. Таблица интегралов
- •3.1.3 Линейность интеграла
- •3.1.4 Приемы интегрирования.
- •3.1.5. Интегрирование "по частям"
- •3.1.7. Интегрирование некоторых типов иррациональностей.
- •3.1.8. Интегрирование некоторых типов тригонометрических выражений.
- •3.2 Определенный интеграл
- •3.2.3. Формула интегрирования по частям
- •3.3. Несобственные интегралы
- •3.4 Приложения определенных интегралов
- •3.4.1. Площадь фигуры.
- •3.4.2. Длина дуги линии
- •3.4.4. Задачи для самостоятельного решения
- •3.5 Криволинейные интегралы
- •3.5.4. Задачи для самостоятельного решения.
3.4.4. Задачи для самостоятельного решения
Найти объем тела, образованного вращением вокруг оси OX фигуры, ограниченной линиями.
1.![]() 2.
2.
![]()
Найти площадь фигуры, ограниченной следующими линиями.
3.
![]() 4.
4.
![]() 5.
5.
![]() .
.
Найти длину линии.
6.
|
7.
|
||
8.
|
9.
|
10.
|
|
3.5 Криволинейные интегралы
3.5.1.
Пусть
сила
![]() перемещает материальную точку М
из начала дуги – точки А,
в конец – точку В
(рис.
3.5.1).
перемещает материальную точку М
из начала дуги – точки А,
в конец – точку В
(рис.
3.5.1).
|
Рис. 3.5.1 |
Он строится по
схеме, приведенной выше, как предел
интегральной суммы скалярных произведений
![]() вектора силы
вектора силы
![]() с вектором "элементарного" (малого)
перемещения
с вектором "элементарного" (малого)
перемещения
![]() .
.
3.5.2. Пусть дуга АВ расположена в области D, где P и Q – непрерывные функции. Если линия L имеет параметрические уравнения
![]() ,
,
причем положение
точки А
соответствует значению
![]() ,
положение B
–
,
положение B
–
![]() ,
то
,
то
![]() .
(3.5.1)
.
(3.5.1)
Если же уравнение
линии L
–
![]() ,
причем
и
– абсциссы соответственно точек А
и В,
то
,
причем
и
– абсциссы соответственно точек А
и В,
то
![]() .
(3.5.2)
.
(3.5.2)
3.5.3.
Смысл формул
(3.5.1),
(3.5.2) состоит
в том, что
выражение
для х
и
у из
уравнений линии подставляем
в подынтегральное выражение
![]() (при этом
вычисляем дифференциалы
и
(при этом
вычисляем дифференциалы
и
![]() ),
после чего производим интегрирование
в границах изменения параметра.
),
после чего производим интегрирование
в границах изменения параметра.
Пример 1. Вычислить
![]()
вдоль дуги АВ астроиды
![]() ,
,
если точке А
соответствует значение параметра
![]() ,
точке В
–
,
точке В
–
![]() .
.
Рис. 3.5.2 |
Решение. Линия, вдоль которой производится интегрирование, изображена на рис. 3.5.2; в нашем случае имеем дугу, расположенную в первой четверти (направление обхода от А к В указано стрелкой). Заметим, что
|
![]() .
.
Значит


![]()
Рис. 3.5.3 |
Пример 2.
Вычислить работу силы
Решение.
Имеем координаты вектора
|
Согласно 3.5.1 достаточно вычислить
![]()
![]() .
.
Подынтегральное выражение в случае есть
![]() .
.
Следовательно, при х, изменяющемся от до , имеем
![]() .
.
3.5.4. Задачи для самостоятельного решения.
Вычислить работу
силы
![]() по перемещению материальной точки вдоль
контура L.
Координаты
,
уравнение линии L,
а также значения x1,
x2
абсцисс (или значения
t1,
t2
параметра t),
соответствующих начальному и конечному
положению точки, указаны.
по перемещению материальной точки вдоль
контура L.
Координаты
,
уравнение линии L,
а также значения x1,
x2
абсцисс (или значения
t1,
t2
параметра t),
соответствующих начальному и конечному
положению точки, указаны.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()

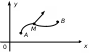 Задача
о вычислении работы
силы
F (совершаемой
вдоль
Задача
о вычислении работы
силы
F (совершаемой
вдоль

