Восстановление периодических сигналов по их амплитудным спектрам с использованием пэвм.

Цель работы: научиться находить спектры периодических сигналов и освоить методику восстановления сигнала по его спектру.

ОСНОВЫ ТЕОРИИ

1. Разложение периодических сигналов на гармонические составляющие (Фурье-анализ).

Для расчета характера распространения сигналов произвольной формы в электрических цепях их, как правило, представляют в виде суперпозиции гармонических составляющих, для которых алгоритмы расчета хорошо известны.

Можно доказать, что любой реальный периодический сигнал, вне зависимости от его формы, можно представить как суперпозицию гармонических сигналов с кратными частотами.

Процесс представления сигналов в виде суммы гармонических колебаний называется Фурье-анализом.

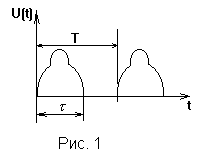
Пусть дан некоторый сигнал U(t) длительностью , который можно рассматривать как повторяющийся с периодом Т > (рис.3).

Тогда функцию U(t) в любой момент времени можно представить в виде:

(1),

где:

(2)

(3) Равенство (1) можно также представить в виде:

(4)

где:

Таким образом, периодический сигнал был представлен в виде суммы некоторой постоянной составляющей U₀ и набора гармонических сигналов с частотами кратными основной частоте ω. Значения коэффициентов U_n в выражении (4) определяют так называемый спектр сигнала.

Спектром сигнала называют соотношение амплитуд (или энергий) составляющих его гармоник кратных частот.

Различают амплитудные и энергетические спектры сигналов. Как известно, энергия любого гармонического колебания пропорциональна квадрату его амплитуды. Поэтому для отображения соотношения вклада различных гармоник в общую энергию сигнала зачастую при изображении спектра сигнала на графиках откладывают зависимость от частоты не амплитуды соответствующей гармоники, а квадрата амплитуды U_n².

Следует отметить, что при изображении спектров сигналов, существенным является не величина амплитуды соответствующей гармоники, а ее соотношение с амплитудами других гармоник. В силу этого при изображении спектров сигналов можно пользоваться не абсолютными величинами амплитуд (или энергии) гармоник, а нормированными, т.е. их отношением, например, к амплитуде (энергии) первой гармоники.

Помимо этого, при описании спектров сигналов чаще используется частота f, а не ω.

На рис. 2 приведены амплитудный (а) и энергетический (б) спектры одного и того же сигнала.

С помощью энергетического спектра можно выделить тот диапазон частот, в котором сосредоточена основная энергия сигнала (например, 90 %). Оказывается, что при передаче гармонических составляющих сигнала с частотами, ограниченными данным диапазоном, можно практически полностью восстановить информацию, переносимую данным сигналом. Такой диапазон частот, внутри которого сосредоточена основная энергия сигнала, называется эффективной шириной спектра сигнала Δf эфф.

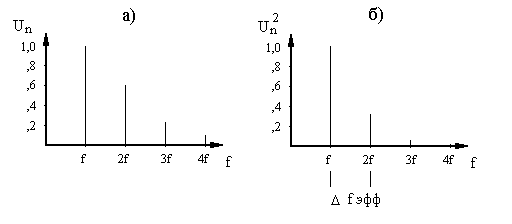
Рис. 2

3. Рассмотрим пример нахождения спектра периодического сигнала. Пусть дан сигнал прямоугольной формы, приведенный на рис.3 и имеющий следующие параметры: А = 1В, Т = 0,01с, τ = 0,005 с.

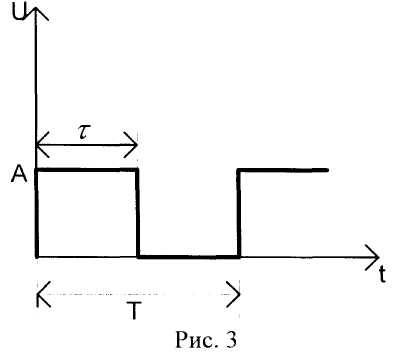
Основная частота спектра

Вычислим коэффициенты спектрального разложения (формулы 1-3) при заданных параметрах:

где n =1, 2, 3, ...

Очевидно, что величина В_n отлична от нуля только при нечетных значениях n, то есть при n=2к-1(к=1,2,3,…).

Окончательно имеем:

Таким образом, рассматриваемый сигнал можно представить как сумму синусоид, с амплитудами U_n=B_n, и частотами, кратными нечетному числу 10² Гц.

На рис.4 приведен энергетический спектр исследуемого сигнала, в котором в качестве интенсивности соответствующей составляющей (гармоники) взяты квадраты амплитуд.

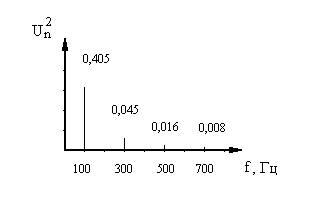
Рис.4

Из рис. 4 видно, что энергия гармоники с частотой 700 Гц составляет всего 0,8% от общей энергии сигнала. Поэтому в качестве эффективной ширины спектра сигнала можно взять диапазон от 0 до 500 Гц.

ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ И ОБРАБОТКА РЕЗУЛЬТАТОВ

1. Найти аналитически коэффициенты спектрального разложения периодического сигнала, заданного преподавателем, используя формулы (1 - 3).

2. Включить персональный компьютер для проверки правильности разложения, восстановив форму сигнала с использованием программы «EUREKA».

3. На диске С:\ войти в директорию EUREKA (C:\EUREKA).

4. Запустить файл eureka.exe.

5. Нажать Esc, для выхода в главное меню, и клавишами влево или вправо выбрать пункт GRAPH; нажать клавишу Enter для входа в ниспадающее меню.

6. В ниспадающем меню выбрать пункт Function. В появившемся окне набрать нужную функцию в виде у = ....

Примечание 1: запись функции осуществляется в стандартном для программирования виде типа: 3sinx = 3*sin(x), sin2x = sin(2*x) и т.д.

Примечание 2: максимальное количество вводимых в строку символов равно 80. Для экономии места необходимо выносит за скобки общие сомножители и использовать как молено меньше скобок. Например, вместо (1/3) *sin(x) лучше писать sin(x)/3.

7. Закончив редактирование вводом ENTER, в том же ниспадающем меню выбрать пункт Plot и задать границы графика (левую и правую соответственно). Рекомендуемые границы - три периода.

8. Увеличение картинки можно получить при нажатии клавиши F5 (Zoom); выход из Zoom осуществляется нажатием клавиши Esc.

9. Проанализировать полученную картинку. В случае ее совпадения с исходным сигналом, предъявить ее преподавателю. В обратном случае, проверить правильность аналитического разложения.

10. Просчитать по формуле (4) численные значения амплитуд гармоник и нарисовать в журнале энергетический спектр сигнала.

11. По полученному спектру найти эффективную ширину спектра сигнала.

12. Написать заключение по работе, приведя в нем аналитические формулы для коэффициентов разложения данного сигнала и эффективную ширину его спектра.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Написать формулы для вычисления спектральных составляющих периодических сигналов.

2. Что называется энергетическим спектром сигнала?

3. Как находится спектр непериодических сигналов?

4. Что такое эффективная ширина спектра сигнала?

Литература

1. Бобровников Л.З. Радиотехника и электроника. М.: Недра, 1984. § 30.

2. Основы радиоэлектроники. Под ред. Г.Д. Петрухина. М.: Изд-во МАИ, 1993. § 8.1.

ЛАБОРАТОРНАЯ РАБОТА №3