3.5.1.2. Проверочный расчет
Проверим соблюдаются ли условия по контактным напряжениям и напряжениям изгиба зубьев.
Условие прочности по контактной выносливости:
Условие прочности по контактной выносливости выполняется.
Условие прочности по изгибной выносливости:
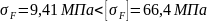
Условие прочности по изгибной выносливости выполняется.
3.5.1.3. Силы в червячном зацеплении
Определим окружную силу на червяке:
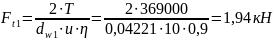
где: η = 0,9 кпд, учитывающий потери в зацеплении, подшипниках;
Осевая сила на колесе равна окружной силе на червяке:
Ft1 = Fa2 = 1,94кН
Осевая сила на червяке равна окружной силе на колесе:
Ft2 = Fa1 = 2,93кН
Определим радиальную силу по формуле:
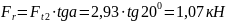
3.5.1.4. Геометрический расчет червячной передачи
Существует ряд геометрических параметров червяка и червячного колеса, которые необходимы для их изготовления.
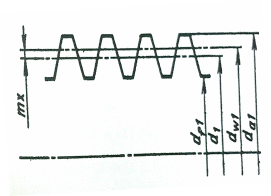
Рис. 10. Основные размеры червяка
Основные размеры червяка:
-делительный диаметр: d1 = т · q = 6,3 16 = 100,8мм
-начальный диаметр: dwl = 98,04мм
-
диаметр вершин витков: da1
= d1
+ 2 · m
= 100,8 + 2
,3
=113,4мм
- диаметр впадин витков: df1 = d1 – 2,4 · m = 100,8– 2,4 6,3 =85,68мм
- делительный угол подъема витков: γ = 14º
- начальный угол подъема витков: γ = 12º
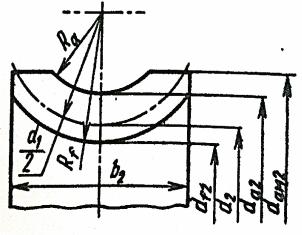
Рис. 11. Основные размеры червячного колеса
Основные размеры червячного колеса:
- делительный диаметр: d2 = 252мм
- диаметр вершин зубьев:
da2 = d2 + 2 · m · (1 + x)= 252 + 2 · 6,3· (1 + 0,2)=292,08мм
- наибольший диаметр колеса:
-
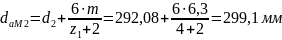
диаметр впадин:
292,8-2*6,3*(1,2-0,2)=280,2мм
- радиусы закруглений колеса:
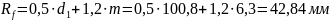
3.7. Математическая модель рычага.
У одноплечного рычага ось расположена на одном из его концов, а силы действующие на него, параллельны но направлены в противоположные стороны (антипараллельны).При работе рычага должно соблюдаться условие прочности:
ϭ≤
[ϭ
]
3.7.1.Работа с математической моделью.
Для снижения усилия, воздействующего на винт при нагружении образца, в данной конструкции используется рычаг.
С помощью метода сечений определим поперечные силы и момент в сечении рычага.
На основании эпюр определим реакцию в точке О и максимальный момент в сечении:
F0 =100 кН; M0 =1000 кН м;
Допустимое напряжение определяется по формуле:
[ϭ]
=
==
235 МПа
Действительное напряжение определяется по формуле (для рычага прямоугольного сечения со сторонами Ь и h, h = 2b):
σ
=
=
Исходя из условия прочности, определим ширину b рычага:
b=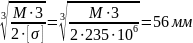
Исходя из того, что в точке О действует сила Ro = 180кН , примем
h = 140 мм при b = 60 мм.
Исходя из этого, произведем проверочный расчет:
Условие прочности соблюдается.
Рис. 13. Расчётная схема рычага.