3.3.2. Проверочный расчет

Проверочный расчет включает в себя соблюдение условия прочности гайки на растяжение.

Условие расчета:

28,3МПа

В итоге:

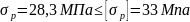
Проверочный расчет витков резьбы гайки на срез включает в себя соблюдение условия статической прочности на срезе:

Рис.9. Схема нагрузки зуба

τ_ср = ;

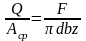где: b – ширина витка у основания для трапецеидальной резьбы, мм;

b = 0,65 · P = 0,65∙9=5,85мм ·

τ_ср = 100000 / (3,14 * 0,0645 * 0,00585 *13,3) = 6,4 Мпа

[τ_ср] = 17,5 МПа

τ_ср = 5,9 МПа < [τ_ср] - условие статической прочности при срезе выполняется

Проверочный расчет бурта гайки на срез.

Назначаем высоту бурта гайки, принимая ее равной: Н_Б = (0,20…0,30)Н_Г

Н_Б =0,3*120=36мм

Условие статической прочности при срезе: τ_ср ≤ [τ_ср];

где [τ_ср] = ;

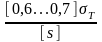[s] = 2…3 - для бронзы;

Примем [τ_ср] равным 17,5 МПа

;

τ_ср = 100000 / (3,14 * (0,09 + (0,002 * 3,14/4) * 36) = 6,28 МПа

τ_ср = 6,28 МПа < [τ_ср] - условие статической прочности при срезе выполняется

3.4.Математическая модель пружины.

Для обеспечения прочности пружины и её длительной работы необходимо чтобы выполнялось условие:

τ [τ₃];

τ-касательное напряжение.

3.4.1. Работа с математической моделью пружины

Примем отношение плеч рычаг равным 0.2 для уменьшения нагрузки на пружину, из этого следует, что - максимальное(рабочие) усилие ( F₂) развиваемое пружиной равно 20 кН.

F₂ = 20 кН = 20000Н

Из ГОСТ 13764-86 выбираем класс и разряд пружины. По типу прикладываемой нагрузки пружины делятся на классы. Первый класс – сжатие и растяжение, нагружение - цилиндрическое. Второй класс – сжатие и растяжение, нагружение цилиндрическое и статическое. Третий класс – сжатие, нагружение циклическое. Исходя из наших условий -

Возьмем пружину 1класса, а по нагрузке определяем разряд – 4.

Пружину будем изготавливать из стали марки 60С2А ГОСТ – сталь горячекатаная, круглая по ГОСТ 2590, ее твердость после обработки от 44 до 51,5 HRC, максимальное касательное напряжение 480 МПа. Стандарт на основные параметры витков пружин – ГОСТ 13769.

Для пружин 1 класса инерционный зазор δ находиться в пределах 0.05÷0.25

Определяем крайние значения максимальной нагрузки (F₃) δ=1-F₂/F₃

F₃ = F₂/1 - δ, F₃ = 20/1-0.05=21,05 F₃=20/1-0.25=26,6.

Максимальная нагрузка (F₃) находится в пределах 21050Н ÷ 26600Н.

Из ГОСТ 13769 – 86 - выбираем пружину позиции номер 150.

Максимальная нагрузка F₃ = 28000Н

Диаметр проволоки d₁ = 32 мм.

Наружный диаметр пружины D₁ = 200 мм

Жесткость одного витка с₁= 2167 Н/мм.

Наибольший прогиб одного витка s₃ = 12, 92 мм.

Определяем средний диаметр пружины D_ср,

D_ср = D₁ - d₁ = 200 – 32 = 168 мм

Для более точного измерения нагрузки, но во избежание выпучивания пружины H/D_ср<3, ход пружины (h) выбираем равным 200 мм.

Ищем общую жесткость пружины с,

с=F₂/h, c = 20000/200 = 100 Н/мм.

Находим число рабочих витков n,

n = c₁/с= 2167/100=21,7; n = 21,7 ≈ 22

Полное число витков n₁ ,

n₁=n+1.5= 22+1.5= 23.5

Теперь вычисляем деформации (s_2, s₃), длины(l) и шаг пружины (t).

s₂ = F₂ /с = 21050/100 = 210 мм

s₃ = F₃/c = 26600/100 = 266 мм

l₃ = (n₁ + 1-n₃) × d = (23.5 + 1-1.5) × 32 = 736 мм

l₀ = l₃ + s₃ = 736 + 266 = 1002 мм

l₂ = l₀ - s₂ = 1002 – 210 = 792 мм

t = s’₃ +d = 12.95 + 32 = 44,95 мм (45)

Длина развернутой пружины по нашим расчетам оказалась

l=3.2×D×n₁=3.2 × 200 × 23.5= 15040 мм.

Сделаем еще один расчет по заданным параметрам и построение пружины в программе Компас.

В результате у нас получились такие же размеры, как и в предыдущем расчете, только немного отличается только длина пружины.

Мы посчитали и у нас получилось - l₀ = 1002 мм

А в компьютере l₀ = 1035 мм