3.2.2. Проверочный расчет

Проверочный расчет винта включает в себя оценку работоспособности винта по критерию статической прочности:

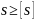
где: s – расчетный (действительный) коэффициент запаса (статической прочности);

[s] – допускаемый (нормативный) коэффициент запаса.

Допускаемый коэффициент запаса [s] для стального винта выбирается из диапазона: [s] = 2,5…3,0.Возьмём s=2.

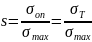
где: 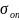- опасное напряжение, МПа;

- действующее напряжение, МПа.

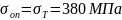
В качестве опасного сечения рассматривается сечение, обладающее наименьшими размерами. При рассмотрении схемы работы винта можно выделить 2 случая:

1) совместное действие ( с учетом T_on = T₀ ).

2) и

Диаметр опасного сечения определятся по формуле:

d_оп  d3 – (3…5)55,5 – 3,5=52 мм

Момент, возникающий от осевой нагрузки, определяется по формуле:

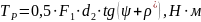
где: ψ – коэффициент трения скольжения;

ρ^* - приведенный угол трения, град.

=

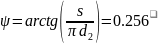
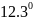
где: 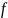– коэффициент трения скольжения;

α₁ – рабочий угол профиля резьбы.

Принимаю:

f = 0,21

где: α = 30º - угол профиля резьбы

=

В итоге:

d_оп = 52мм

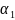= 15^о

= 12,3^о

ψ =

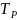= 666 Н^* м

Момент трения возникающий в опорной пяте определяется по формуле:

Произведем расчет коэффициента запаса для двух случаев:

1) 113МПа ( = 62МПа, =5,5 МПа)

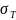= 380МПа

S = ( 380 10⁶)/(32 10⁶) =11,8

2) 32МПа ( =0 МПа, =19 МПа)

= 380 МПа

S = (380 10⁶ )/(32 10⁶ ) = 11,8

В итоге:

S = 3,36˃ [S] = 2,5…3 – условие статистической прочности выполняется.

S = 11,8˃ [S] = 2,5…3 – условие статистической прочности выполняется.

3.3. Математическая модель гайки

Обуславливающая работоспособность гайки математическая модель состоит из нескольких условий:

• условие прочности гайки в опасном сечении, ;

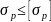• условие прочности гайки на смятие по опорной кольцевой поверхности,

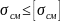
• условие прочности витков резьбы на срез

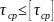
• условие непроворачиваемости гайки в корпусе Тр < Ттр мах

3.3.1. Работа с математической моделью гайки

Определение посадочного диаметра гайки D_Г.

Критерий работоспособности – статическая прочность гайки при растяжении.

Условие расчета:

где: – допустимое напряжение, МПа;

- действительное напряжение, МПа.

где: - пределы прочности текучести для бронзы, МПа;

- запас прочности

Принимаю:

= 2…3 для бронзы

= 33 МПа

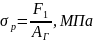
где: 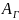- площадь опасного сечения гайки (при растяжении), м²;

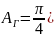
Определим расчетное значение посадочного диаметра гайки 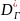, решая исходное неравенство:

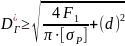
=89мм

Далее, расчетное значение округляем до стандартного из ряда предпочтительных чисел по ГОСТ 6636-69.

90

Определение диаметра бурта гайки D_Б

Условие расчета: σ_см ≤ [σ_см] ,где σ_см = (0,6…0,8) σ_Т – для бронзы;

σ_см =

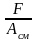
[σ_см] = 60 МПа –для бронзы;

где А_см =

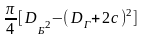
- площадь смятия с учетом заходной фаски корпуса

с = (2…2,5)х45⁰;

Определим расчетное значение бурта гайки D_Б*, решая исходное неравенство:

D_Б* = ;

D_Б* = ((4* 100000 / 3,14 * 60 * 10⁶) + (0,09 + (0,002 * 3,14/4))² )^0,5 = 102,5 мм

Далее, расчетное значение округляем до стандартного из ряда предпочтительных чисел по ГОСТ 6636-69.

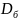=105 мм

:

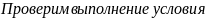D_Б ≥ D_Г + 10мм

D_Б = 105 ≥ 100