3.1. Математическая модель рукоятки

Для обеспечения работоспособности рукоятки, математическая модель состоит из условий:

• условие прочности на изгиб: ;

• условие равновесия:

3.1.1. Работа с математической моделью рукоятки

Проектировочный расчет рукоятки заключается в определении ее расчетной длины. Расчетная длина рукоятки определяется из условия:

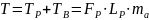, Нм

Момент T_Р определяется, как момент необходимый для предварительного сжатия пружины перед работой экспериментальной установки.

В зависимости от частоты и длительности работы установки, сила воздействия на рукоятку F_Р принимается по следующим соображениям:

F_Р = 120.. .200 Н - при длительном и частом режиме работы;

F_Р = 250.. .300 Н - при кратковременном режиме работы;

m = 1 или 2.

Желательно, чтобы L_Р была не более 1200 мм, в этом случае принимаем m = 2

Общая длина рукоятки:

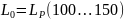, мм

В результате расчетов получаем:

Т_Р = 144 Н*м

Т = 288 Н*м

m = 2

F_P = 180 Н

L_P = 400 мм

L₀ = 500 мм

L_И = 350 мм

Критерием работоспособности рукоятки в данном механизме является статическая прочность при изгибе.

Условие прочности выглядит следующим образом:

где: - напряжение при изгибе, МПа;

- допускаемое напряжение при изгибе, МПа.

- предел текучести, МПа;

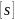- запас прочности, выбирается из соотношения

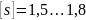
Напряжение при изгибе определяется по формуле:

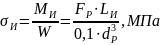
Из выше перечисленных формул выразим диаметр ручки:

Полученное значение диаметра ручки округляется до стандартного значения, из ряда предпочтительных чисел по ГОСТ 66336-69.

В результате расчетов получаем:

= 230 МПа (для материала Сталь Ст3);

= 1,6

=

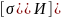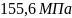
= 350 мм

= 20 мм

3.1.2. Проверочный расчет по условию прочности на изгиб

В результате проверочного расчета получаем:

= 155,6 Мпа

= 76,3 Мпа

– условие прочности выполняется

3.2 Математическая модель винта

Интенсивность изнашивания зависит от: нагрузки на единицу площади, материала, температуры, наличия смазки, шероховатости поверхности, скорости скольжения.

Для того чтобы деталь была износостойкой, необходимо, чтобы интенсивность изнашивания была не очень высокой, что гарантирует её длительную работу.

Поэтому в упрощенном виде условие износостойкости можно записать в виде:

3.2.1. Работа с математической моделью винта

Проектировочный расчет винта включает в себя определение стандартных параметров заданной резьбы: диаметров и шага; с учетом критериев работоспособности, а именно износостойкости винтовой пары

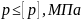
где: р – удельное давление на витках резьбы, МПа;

[р] – допускаемое удельное давление на витках резьбы, МПа.

Допускаемое удельное давление в витках резьбы [р] для пары материалов сталь незакалённая - бронза оловянная определяется из диапазона [p]=8..10 МПа.

Принимаю: [р] = 10 МПа.

Рядом параметров резьбы можно пренебречь, учитывая, что они лишь повышают работоспособность, например: углом профиля резьбы (полагая, что α=0, т.е. имеем прямоугольную резьбу); полагаем, что нагрузка на сопряженные витки резьбы распределяются равномерно.

Тогда удельное давление можно определить в общем виде из следующего выражения:

где: F_n - нормальная сила, действующая в витках резьбы, Н;

А_n - площадь соприкосновения витков резьбы винта (гайки), мм²;

F1 - осевая нагрузка на винтовую пару (усилие, которое передается от рычага непосредственно винту и пружине), Н;

А - площадь проекции одного витка резьбы на плоскость, перпендикулярную к оси винта, мм² ;

z - количество витков.

где: d₂ - средний диаметр резьбы, мм;

h - высота профиля резьбы, мм.

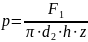
Введём в формулу удельного давления вспомогательные коэффициенты γ₁ и γ₂:

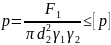
где: γ₁ - коэффициент рабочей высоты профиля резьбы;

γ₂ - коэффициент высоты гайки.

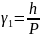
где: Р – шаг резьбы, мм.

Для трапецеидальной резьбы γ₁ = 0,5.

где: Н_Г – высота гайки.

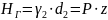
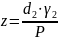
Коэффициент высоты гайки выбирается из диапазона

Выбираем

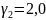
Расчетное значение среднего диаметра резьбы 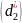определяется из выражения:

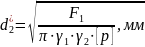
d₂^* = (100000 / 3,14 * 0,5 * 2 * 10 * 10⁶)^0,5 =56мм

В соответствии с найденным расчетным значением 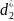, по ГОСТ 9484-81 выбираем стандартные параметры заданной резьбы:

d₂ = 60мм

d = 64.5мм

d₃ = 55.5мм

P_Ш = 9мм

Исходя из полученных данных, получаем ряд величин по формулам:

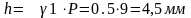
Hг= _{2 *} d2 = 120 мм

Z= Нг / Рш =13,3

Проверка найденного значения по условию износостойкости:

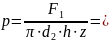8,86Мпа

P = 8,86 МПа 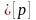= 10 МПа – условие износостойкости выполняется

Износостойкость винтовой пары обеспечена.