2.4. Распознаватели

Второй способ задания формальных языков основан на применении распознавателей [1-3]. Распознаватель - это некоторый алгоритм, который выполняет анализ терминальных цепочек и устанавливает, является ли анализируемая цепочка синтаксически правильной. Если распознаватель выдает ответ - "да", то говорят, что он допускает цепочку и цепочка называется допустимой. Язык, определяемый распознавателем - это множество цепочек, которые он допускает.

Распознаватель можно представить в виде абстрактного устройства, структура которого показана на рис. 2.1.

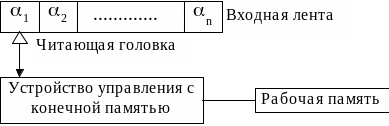
Рис. 2.1

Входная лента-это линейная последовательность ячеек, каждая из которых содержит один символ некоторого входного алфавита  . Читающая головка в каждый момент обозревает один символ на входной ленте. За один шаг работы распознавателя головка может сдвинуться на одну ячейку вправо, влево или остаться неподвижной. Мы будем рассматривать только односторонние распознаватели, у которых читающая головка никогда не сдвигается влево.

Рабочая память-это некоторое хранилище данных произвольной организации.

Управляющее устройство(УУ) с конечной памятью -основная часть распознавателя, определяющая его поведение.

Работа распознавателя состоит из тактов, а каждый такт из следующих действий:

входная головка сдвигается вправо или остается на месте;

в рабочую память помещается некоторая информация;

изменяется состояние УУ.

Поведение распознавателя удобно описывать в терминах конфигураций. Конфигурацию можно рассматривать как моментальный снимок распознавателя, на котором отражено состояние всех его элементов (состояние УУ, положение читающей головки и др.)

УУ (и сам распознаватель) называется детерминированным, если из текущей конфигурации в результате выполнения такта распознаватель может перейти только в одну очередную конфигурацию, и недетерминированным - если переход возможен в одну из множества конфигураций.

Конечные автоматы. Простейшими из распознавателей являются конечные автоматы(КА).

Определение. КА - это пятерка: ,

где Q- конечное множество состояний КА;

- конечное множество допустимых входных символов (входной алфавит);

 - функция переходов (отображение) Q в (Q);

- начальное состояние;

F- множество заключительных состояний.

Функция переходов  задает допустимые последовательности переходов КА из одного состояния в другое, в зависимости от читаемых автоматом символов.

Определение. Пара называется конфигурацией КА, при этом конфигурация называется начальной, а ( , e), где F ,- конечной конфигурацией. 

Такт работы КА можно представить бинарным отношением , заданным на конфигурациях.

Определение. Определим бинарное отношение следующим

образом:

если для всех a  , w   ^*. 

Обычным образом вводятся отношения ^k, ^*, ⁺,при этом:

запись с ⁰ означает, что ;

запись с ^k означает, что существует последовательность конфигураций КА такая, что c ⁱ c ⁱ⁺¹ для 0 i  k-1, т.е. соответствует траектории из k тактов;

запись с ^* соответствует некоторой траектории КА, переводящей его из , за некоторое число(включая ноль) тактов;

запись соответствует некоторой траектории КА, переводящей его из , за некоторое число k1 тактов.

Говорят, что автомат М допускает цепочку w, если

(q₀ , w ) ^* (q,e) для некоторого qF. Другими словами, цепочка допускается, если существует траектория, переводящая КА из начальной конфигурации в заключительную, в результате выполнения которой эта цепочка оказывается прочитанной.

Языком, определяемым автоматом М, называется множество

цепочек L(M):

L(M)={w | w ^ и (q₀ , w ) ^* (q,e) для некоторого qF }.

Пример 2.14. M=({p,q,r},{0,1}, ,q,{r})

Функцию переходов можно задать в явном виде(в виде функции), в виде таблицы или в виде графа переходов, которые приведены ниже.

В явном виде:

В виде таблицы:

Таблица 2.1.

B виде графа переходов (рис. 2.2)

Рис. 2.2

При задании КА в виде таблицы на пересечении каждой строки и столбца записывается символ состояния (или множество состояний), в которое переходит автомат из текущего состояния (соответствующего строке), при чтении входного символа (соответствующего столбцу).

При изображении в виде графа, его вершины помечаются состояниями автомата, а дуги — значениями входных символов. Каждая дуга (p,q), помеченная входным символом a, означает, что при чтении a в состоянии p автомат переходит в состояние q. Кроме того, начальное и заключительное состояния выделяют из других состояний КА так, как это показано выше.

Пусть на входе КА цепочка w=01001, тогда автомат выполнит следующую последовательность тактов:

(p,01001)  (q,1001)  (p,001)  (q,01)  (r,1)  (r,e).

Поскольку (r,e)-заключительная конфигурация, цепочка w допускаеся.

Пусть w=10101, тогда

(p,10101)  (p,0101)  (q,101)  (p,01)  (q,1)  (p,e)

и цепочка w не допускается (т.к. p - не заключительное состояние).

Пример 2.15. M= ({q₀,q₁,q₂,q₃,q_f},{1,2,3}, ,q₀,{q_f}), функция переходов  задана табл.2.2.

Таблица 2.2.

Состояние		Вход
	1	2	3
q0	{ q0,q1}	{ q0,q2}	{ q0,q3}
q1	{ q1,qf}	{q1}	{q1}
q2	{q2}	{ q2,qf}	{q2}
q3	{q3}	{q3}	{ q3,qf}
qf			

Автомат М проанализирует входную цепочку w=12321 по траектории, приведенной на рис.2.3. Данный автомат является недетерминированным и его траектория имеет вид дерева. Если хотя бы один путь в этом дереве приводит к заключительной конфигурации, то цепочка считается допустимой, следовательно, w=12321 -допустимая цепочка (т.к. - заключительная конфигурация).

Определение. Пусть M=(Q,,,q₀,F) - недетерминированный КА. Назовем его детерминированным, если множество (q,a) содержит не более одного элемента для всех q  Q и a  . 

Так, КА в примере 2.14 является детерминированным. Недетерминированные КА сложно реализовать на обычных ЭВМ, так как эти автоматы содержат параллельные процессы. В теории автоматов доказывается, что класс языков, определяемых недетерминированными КА, совпадает с классом языков, определяемых детерминированными КА, что имеет большое прикладное значение при программной реализации КА.

Рис.2.3.