Сортировка посредством слияния списков

Алгоритмы слияния имеют два существенных недостатка:

1. Большой расход памяти для вспомогательной рабочей области.

2. Необходимость большого числа перемещений записей.

Э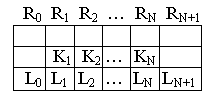 ти недостатки можно устранить, создав из сортируемого файла подобие связанного списка, для чего каждая запись R_i должна иметь “поле связи” L_i, в котором будет храниться № записи, следующей за данной записью в порядке возрастания ключей.

После сортировки L₀=№ записи с наименьшим ключом.

Алгоритм L.

Предполагается, что записи R₁,…,R_N содержат ключи k₁,…,k_N и поля связи L₁,…,L_N, в которых могут храниться числа от -(N+1) до (N+1). В начале и в конце файла имеются искусственные записи R₀ и R_N+1 с полями связи L₀ и L_N+1. Этот алгоритм сортировки списков устанавливает поля связи таким образом, что записи оказываются связанными в возрастающем порядке.

После завершения сортировки L₀ указывает на запись с наименьшим ключом, при 1≤k≤N связь L_k указывает на запись, следующую за R_k , а если R_k – запись с наибольшим ключом, то L_k=0. В процессе выполнения этого алгоритма записи R₀ и R_N+1 служат “головами” двух линейных списков, подсписки которых в данный момент сливаются.

Отрицательная связь означает коненц подсписка, о котором известно, что он упорядочен; нулевая связь означает конец списка. Предпологается, что N≥2.

Через “|L_s|←p” обозначена операция присвоить L_s значение р или –p, сохранив прежний знак L_s.

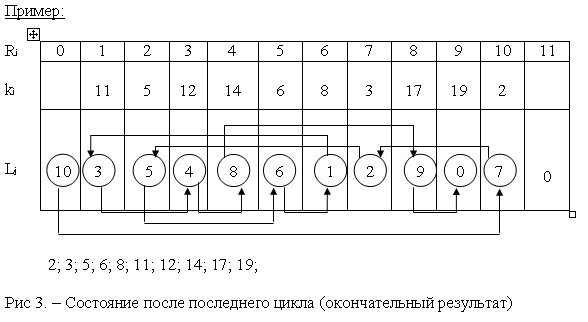
L1. [Подготовить два списка.] Установить L₀←1, L_N+1←2, L_i← -(i+2)

при 1≤i≤N-2 и L_N-1←L_N←0.

Мы создаём два списка, содержащие соответственно записи

R₁,R₃,R₅,… и R₂,R₄,R₆,…; отрицительные связи говорят о том,

что каждый упорядоченный “подсписок” состоит всего лишь из

одного элемента. Другой способ выполнить этот шаг, извлекая пользу из

упорядоченности, которая могла присутствовать в исходных

данных.

L2. [Начать новый просмотр.] Установить s←0, t←N+1, p←L_s, q←L_t.

Если q=0, то работа алгоритма завершена.

При каждом просмотре p и q пробегают по спискам, которые

подвергаются слиянию; s обычно указывает на последнюю

обработанную запись текущего подсписка, а t – на конец только

что выведенного подсписка.

L3. [Сравнить k_p : k_q.] Если k_p>k_q, то перейти к L6.

L4. [Продвинуть p.] Установить |L_s|←p, s←p, p←L_p. Если p>0, то возвратиться к шагу L3.

L5. [Закончить под список.] Установить L_s←q, s←t. Затем установить t←q и q←L_q один или более раз, пока не станет q≤0, после чего перейти к шагу L8.

L6. [Продвинуть q.] (Шаги L6 и L7 двойственны по отношению к L4 и L5.) Установить |L_s|←q, s←q, q←L_q. Если q>0, то возвратиться к шагу L3.

L7. [Закончить подсписок.] Установить L_s ←p, s←t. Затем установить

t←p и p←L_p один или более раз, пока не станет p≤0.

L8. [Конец просмотра.] (К этому моменту p≤0 и q≤0, так как оба

указателя подвинулись до конца соответствующих подсписков.)

Установить p← -p, q← -q. Если q=0, то установить |L_s|←p, |L_t|←0

и возвратиться к шагу L2. В противном случае возвратиться к

шагу L3.

9. Алгоритмы поиска данных. Последовательный, двоичный, блочный, интерполяционный, Фибоначчиев поиск.

В алгоритмах поиска присутствует аргумент поиска К. Задача в том, чтобы отыскать запись, имеющую К своим ключом.

Классификация: 1) группы последовательного поиска 2) поиск посредством сравнения ключей (поиск в таблице)(бинарный, Фибоначчи) 3)поиск цифровой 4) хеширование 5) поиск по вторичным ключам.

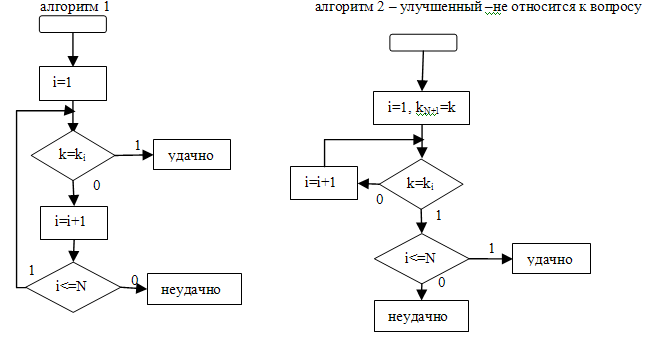
Последовательный - наиболее простой способ отыскания записи. Состоит в последовательном просмотре и сравнении их ключей с данными.

Бинарный поиск Разыскивается аргумент К в таблице R₁....R_N, у которых ключи упорядочены k₁<=...<=k_N.

Идея: 1) Сравнить К со средним ключом в таблице. Результат сравнения определит в какой половине находится запись. Применяя к ней туже процедуру, через log ₂N будет установлено есть ли такая запись:

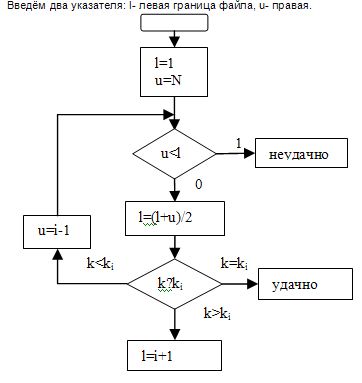
| 7 | 11 | 12| 15 | 18| 19 | 21 | 22 | 25 | 27 | 31 | 35 | 40 |

l u

Метод Фибоначчи. N<=F_k+1 - 1

N – количество элементов в массиве;

k – порядковый номер в дереве Фибоначчи;

F_k+1 – число Фибоначчи;

1. Если k= 0 или k= 1, то корень дерева равен 0.

2. Если k>= 2, то корнем является число F_k, левое F_k-1, правое F_k-2

| 0 | 1 | 1| 2 | 3| 5 | 8 | 13 | 21 | 34 |

Алгоритм предназначен для поиска аргумента К в табл записей R1,R2,…,Rn, распсположенных в порядке возрастания ключей К1<K2<…<Kn. Предполагается, что N+1 есть число Фибоначчи F_k+1.Подходящей нач.установкой данный метод можно сделать пригодным для любого N.В алгоритме p и q-последов числа Фибоначчи.

Представьте себе, что Вы ищете слово в словаре. Если нужное слово начинается с буквы 'А', вы наверное начнете поиск где-то в начале словаря. Когда найдена отправная точка для поиска, ваши дальнейшие действия мало похожи на рассмотренные выше методы.Если Вы заметите, что искомое слово должно находиться гораздо дальше открытой страницы, вы пропустите порядочное их количество, прежде чем сделать новую попытку. Это в корне отличается от предыдущих алгоритмов, не делающих разницы между 'много больше' и 'чуть больше'. Мы приходим к алгоритму, называемому интерполяционным поиском: Если известно, что К лежит между K_l и K_u, то следующую пробу делаем на расстоянии (u-l)(K-K_l)/(K_u-K_l) от l, предполагая, что ключи являются числами, возрастающими приблизительно в арифметической прогрессии. Интерполяционный поиск работает за log log N операций, если данные распределены равномерно. Как правило, он используется лишь на очень больших таблицах, причем делается несколько шагов интерполяционного поиска, а затем на малом подмассиве используется бинарный или последовательный варианты.

Блочный поиск Если элементы упорядочены по ключу, то при сканировании списка не требуется чтение каждого элемента. Компьютер мог бы, например, просматривать каждый n-ный элемент в последовательности возрастания ключей. При нахождении элемента с ключом, большим, чем ключ, используемый при поиске, просматриваются последние n-1 элементов, которые были пропущены. Этот способ называется блочным поиском: элементы группируются в блоки, и каждый блок проверяется по одному разу до тех пор, пока ни будет найден нужный блок. Вычисление оптимального для блочного поиска размера блока выполняется следующим образом: в списке, содержащем N элементов, число просмотренных элементов минимально при длине блока, равной N. При этом в среднем анализируется N элементов.

10. Хеширование, хеш-функции. Способы разрешения коллизий.

Хеширование – есть один из методов поиска. Основная проблема хеширования – это проблема однозначности, т.к. возможно совпадение адресов при несовпадающих ключах: ki≠kj.

Коллизия (h(ki)=h(kj)) – это совпадение вычисленных значений адресов в 2-х или более записях файла, имеющих различные значения ключа. Хеширование – это способ вычисления адреса, при которых функция расстановки выдаёт различные значения для различных входных данных.

Существует специальная программа разрешения коллизий

Хеш-функция – это функция расстановки, основанная на использовании метода хеширования и обеспечивающая равномерное заполнение файла.

Хеш-функция. Предположим, что хеш-функция h(k) имеет M различных значений, удовлетворяющих условию 0≤ h(k)<М для всех k. В реальном файле очень много почти одинаковых ключей, поэтому желательно выбрать хеш-функцию, рассеивающую их по таблице. Наиболее распространённые методы:

а)деления; функция хеширования определяется h(k)=k mod M, где k – ключ, М – количество свободных ячеек таблицы(не должно быть кратным 3 и не должно быть равным степени основания СИ ЭВМ).

б)умножения; h(k)=МАk/W,

умножение ключа k на некоторую фиксированную константу А и выбор нескольких цифр из середины результата, W – максимальное число; А – константа не имеющая общих делителей с W, кроме 1;

М равно степени 2.

в) Метод середины квадрата (midsquare technique) предусматривает преобразование ключа в целое число, возведение его в квадрат и возвращение в качестве значения функции последовательности битов, извлеченных из середины полученного числа. Предположим, что ключ есть целое 32-битное число. Тогда следующая хеш-функция извлекает средние 10 бит возведенного в квадрат ключа.

Методы разрешения коллизий.

Разрешение коллизий "открытой адресацией" состоит в том, чтобы полностью отказаться от ссылок и просто просматривать один за другим различные элементы таблицы, пока не будут найдены ключ K или свободная позиция. Не плохо было бы иметь правило, согласно которому каждый ключ K определяет последовательность проб, т.е. последовательность позиций в таблице, которые нужно просматривать всякий раз при вставке или поиске K. Если мы, используя определяемую K последовательность проб, натолкнемся на свободную позицию, то можно сделать вывод, что K нет в таблице, так как та же последовательность проб выполняется каждый раз при обработке данного ключа. Этот общий класс методов У. Петерсон назвал открытой адресацией.(метод случайного зондирования, метод линейного зондирования, метод квадратичного зондирования)

.Метод цепочек. В процессе хеширования возможно появление одинаковых адресов для различных ключей. Способ разрешения таких коллизий состоит в поддерживании М связанных списков по одному на каждый возможный хеш-адрес. Все связи должны содержать поля связей и нужно образовать массив ссылок, которые будут являться головами списков HEAD[i], где i÷1→М. После хеширования ключа выполняется последовательный поиск в списке с номером h(k).

Метод раздельных цепочек

Ключ k one two three four five six seven

Адрес h(k) 3 1 4 1 5 9

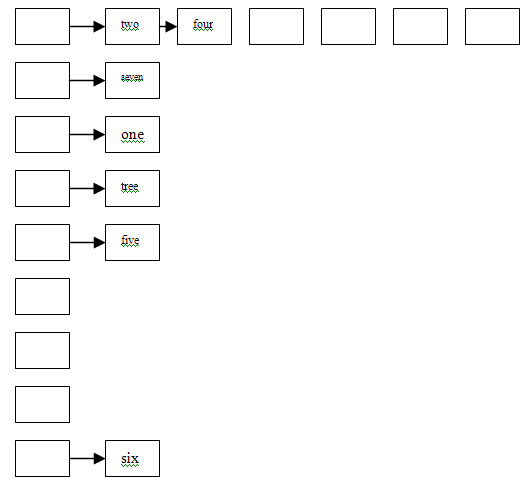
Метод по рассеянной таблицей со сросшимися цепочками. Этот алгоритм позволяет отыскать в таблице из N элементов ключ k. Если ключа нет и таблица не полная, то ключ k вставляется в неё. Элементы таблицы TABLE[i], где 0≤і≤М. Эти элементы могут быть 2-х типов: заняты и свободны. Занятый узел содержит ключевое поле KEY[i], поле связи LINK[i] и т.д.

Метод сросшихся цепочек

two
seven
one
three
five
six
four

Алгоритм для этого метода: М – размер таблицы; i – массив элементов; R – вспомогательная переменная.

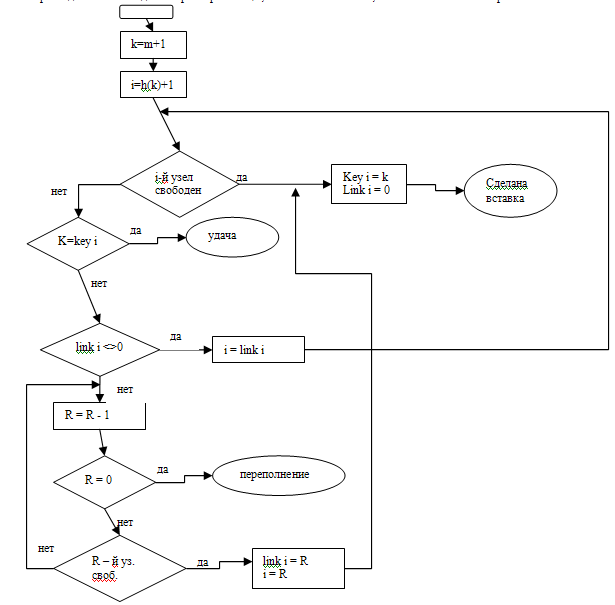
Алгоритм использует хеш-функцию h(k). Для облегчения поиска свободного пространства используют R (R= М+1 для пустой таблицы). Узел TABLE[0] – всегда свободен.

Метод свертывания: Ключ разбивается на части,каждая из которых имеет длину требуемого адреса

187|249|653

Затем части складываются и не учитывается перенос в старшем разряде

187

+ 249

653__

1089 -результат равен 89

Метод гранич свертывания:инвертируются цифры в крайних границах ключа

78

+ 24

_356__

386- результат

Метод преобразования систем исчисления: Ключ, представленный в системе исчисления q, где q=2 или 10 обычно

p>q

возьмем число: 530476 (ключ в десятичном виде)

530476=5*11⁵+3*11⁴+0*11³+4*11²+7*11¹=849745

Отсекаем 3 разряда в правой части

Должно попасть в интервал 000 – 999

745-попал в интервал