Метод Шелла

Некоторое улучшение метода сортировки простыми включениями было предложено Д.Шеллом в 1959 году.

Идея метода: Сортируются группы записей, отстоящих друг от друга на заданном расстоянии(8). После сортировки всех таких групп, сортируются группы записей, отстоящих на меньшее расстояние(4) и т.д., пока не дойдём до расстояния равному 1.

Существует формула для расчёта приращений:

n – количество записей;

t – количество приращений;

t=[log3n]

t=[log3n]-1;

h_t=1;

h_{k -1}=3*h_k+1,

где h – приращение.

Получаем ряд приращений 1,4,13,40,121…

Пример:

n=27; t=3;

h₃=1; h₂=4; h₁=13.

Пример:

4. (4),(2),(1) – приращения

44 55 12 42 94 18 6 67 4 - сортировка

44 18 6 42 94 55 12 67 2 - сортировка

6 18 12 42 44 55 94 67 1 - сортировка

6 12 18 42 44 55 67 94 результат

Затраты, которые требуются для сортировки n элементов с помощью алгоритма Шелла пропорциональны n^1,2.

Методы обмена

Это семейство методов, в которых предусматриваются систематические обмены местами между элементами пар, в которых нарушена упорядоченность до тех пор, пока массив не будет отсортирован.

Быстрая сортировка

(обменная сортировка с разделением)

Это улучшенный метод, основанный на принципе обмена. Неожиданно оказалось, что усовершенствованный «пузырёк» даёт лучший результат из всех известных до настоящего времени методов сортировки. Он обладает столь блестящими характеристиками, что его изобретатель Хоар окрестил его “быстрой сортировкой”, QuickSort (1962г.).

В методе Бетчера последовательность сравнений предопределена; она не зависит от фактического состояния файла (т.е. от того, насколько он уже упорядочен). Разумно предположить, что метод сортировки будет эффективнее, если последовательность сравнений элементов зависит от результатов предыдущих сравнений (т.е. будет учитываться состояние файла).

Q-sort основана на том факте, что для достижения наибольшей эффективности желательно производить обмены элементов на больших расстояниях.

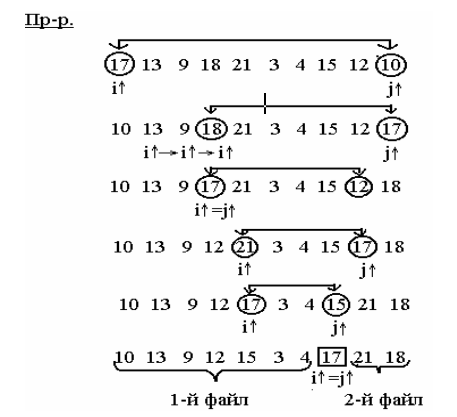
Алгоритм.

массив

i=1 → ← j=N

Пусть имеются два указателя i и j. Причём вначале: i=1, j=N.

Сравним ki и kj (ki : kj).

Если обмен не нужен, то уменьшаем j на 1 и повторяем этот процесс.

После первого обмена увеличим i на 1 и будем продолжать сравнения, увеличивая i, пока не произойдёт ещё один обмен, тогда уменьшим j и т.д., пока не станет i=j. К этому моменту запись Ri(Rj) займёт свою окончательную позицию, и исходный файл будет разделён на два подфайла:

(R₁,…R_{i -1})R_i(R_i+1,…,R_n).

Эти подфайлы надо сортировать независимо (тем же методом).

В процессе сортировки образуется множество подфайлов, которые можно сортировать параллельно, независимо друг от друга.

Если подфайлы будут образовываться последовательно, то информация о неотсортированных подфайлах сбрасывается в стек. При этом целесообразно при образовании двух подфайлов в стек скидывать больший из них.

Каждый из подфайлов сортируют методом Q-sort за исключением очень коротких.

Обменная поразрядная сортировка

Вместо того чтобы сравнивать между собой два ключа, в этом методе проверяется, равны ли нулю или единице отдельные биты ключа от старшего бита к младшему. Рассмотрим метод, напоминающий метод быстрой сортировки, но использующий двоичное представление ключей. Здесь, вместо арифметических сравнений ключей проверяется, равны ли нулю или единице отдельные биты ключей.

В общих чертах идея метода следующая:

I этап. Файл сортируется по старшему значащему биту ключа так, что все ключи, начинающиеся с нуля, оказываются перед всеми ключами, начинающимися с единицы. Для этого надо найти самый левый ключ k_i, начинающийся с единицы и самый правый k_j, начинающийся с нуля, после чего, записи R_i и R_j меняются местами. Процесс повторяется до тех пор, пока не станет i>j.

II этап. Обозначим через F₀ множество элементов, начинающихся с нуля, а через F₁ – остальные. Применим к F0 обменную поразрядную сортировку (начинаем теперь со второго бита слева) до тех пор, пока множество F₀ не будет полностью отсортировано. Затем проделываем то же самое с множеством F₁. Как и при быстрой сортировке, для хранения информации о подфайлах, ожидающих сортировку, можно воспользоваться стеком. Стратегию формирования стека здесь применяют другую: В стек помещать не больший из подфайлов, а правый подфайл, при этом элементы стека (r,l) означают, что подфайл с правой границей r ожидает сортировку по биту l, левую границу можно не запоминать, она всегда задана неявно, так как файл обрабатывается слева на право.

Алгоритм:

Записи от 1-й до N-й R₁,R₂,…,R_N переразмещаются на том же месте. После завершения сортировки их ключи будут упорядочены

k₁≤…≤k_n

Предполагается, что все ключи – это m-разрядные двоичные числа:

а₁,а₂,…,а_m .

R1 [Начальная установка.] Опустошить стек, установить l←1,

r←N,b←1.

R2 [Начать новую стадию.] Сортируется подфайл записей со

следующими границами:

R_l≤…≤R_r по биту b.

По смыслу алгоритма l≤r; если r=l, то перейти к R₁₀, в

противном случае i←l,j←r.

R3 [Проверить ki на единицу.] Проверить бит b ключа ki на единицу.

Если (k_i)_b=1, то перейти к шагу R6.

R4 [Увеличить i.] Если i≤j, то возвратиться к R3, иначе к шагу R8.

R5 [Проверить kj+1 на ноль.] Проверяется бит b ключа k_j+1.

Если (k_j+1)_b=0, то перейти к шагу R7.

R6 [Уменьшить j.] Уменьшить j на 1. j←j-1.Если i≤j, то перейти к шагу R₅, иначе к R₈.

R7 [Поменять местами записи R_i и R_j+1.] Поменять местами R_i и R_j+1, затем перейти к шагу R4.

R8 [Проверить особые случаи.] К этому моменту стадия разделения

завершена, i=j+1, бит b ключей от k_l до k_j равен нулю, а бит ключей от k_i до k_r равен единице. Увеличить b на 1. Если b<m,где m – число бит,

или меньше, то перейти к шагу R10. Это значит, что подфайл

R_l…R_r отсортирован. Если в файле не может быть равных ключей, то такую проверку можно не делать. Иначе, если j<1 или j=r, возвратиться к шагу R2 (все просмотренные биты оказались равными соответственно

единице или нулю).

Если j=l, то увеличить l на 1 и перейти к шагу R2 (встретился

только один бит, равный нулю).

R9 [Поместить в стек.] Поместить в стек пару (r,b), затем установить

r←j и перейти к R2.

R10 [Взять из стека.] Если стек пуст, то сортировка закончена, иначе

установить l←r+1, взять из стека элемент (r’,b’), установить

r←r’,b←b’ и возвратиться к шагу R2.

Для хранения “информации о границах” подфайлов, ожидающих сортировки мы воспользуемся стеком.

Вместо того, чтобы сортировать в первую очередь наименьший из подфайлов, удобно продвигаться слева направо, т.к. размер стека в этом случае никогда не превзойдёт числа битов в сортируемых ключах.

8. Сортировка. Методы выбора и слияния. Простой, квадратичный выбор. Выбор из дерева. Двухпутевое слияние. Метод слияния списков.

Простой выбор

Простейшая сортировка, построенная на этой идее, состоит из следующих шагов:

1. Найти наименьший ключ, после чего выбрать соответствующую

ему запись и переслать её в начало некоторой пустой области

памяти (т.н. область вывода).Так, как операция ввода соответствует чтению данных и не

удаляет физически запись из сортируемого файла, то удаление имитируется заменой ключа на значение “∞” (∞ по предположению больше любого реального ключа.)

2. Повторить шаг 1. На этот раз будет найден ключ, наименьший из оставшихся.

3. Повторять шаг 1 до тех пор, пока не будут выбраны все N записей.

Этот метод требует наличия всех исходных элементов до начала сортировки, а элементы вывода он порождает последовательно, один за другим. Картина по существу противоположна методу вставок, в котором исходные элементы должны поступать последовательно, но вплоть до завершения сортировки ничего не известно об окончательном выводе.

Описанный метод требует N-1 сравнений, каждый раз, когда выбирается очередная запись.

П ример: Сортируемый файл Область вывода

Недостатки этого метода очевидны, если использовать последовательное размещение записей файла в памяти:

• большое число сравнений N(N-1);

• необходима дополнительная память.

Этот метод можно модифицировать следующим образом:

выбранную на очередном шаге запись помещать в тот же самый файл на место, соответствующее месту в случае использования области вывода, а находящуюся на этом месте запись перенести на место выбранной. При этом отпадает необходимость в использовании ∞ и количество просматриваемых элементов с каждым шагом сокращается на 1.