Структуры и алгоритмы обработки данных

1. Линейные списки – стеки, очереди, деки. Набор процедур для работы со связанным стеком, очередью.

Динамические структуры представляются списковыми структурами. Список-совокупность связанных узлов. Эти узлы имеют внутреннюю структуру. Они связаны между собой, причем каждый элемент характеризуется одним и тем же набо­ром полей. Определенный таким образом список называют так­же линейным списком вследствие линейной упорядоченности его элементов. Упорядоченность элементов списка может за­даваться неявно путем последовательного расположения его элементов как в логической структуре, так и в памяти машины. Такой список будем называть последовательным. упорядоченность элементов может задаваться с помощью специальных указателей, располагаемых в элементах и дающих возможность для каждого элемента определить его предше­ственника или последователя. Такая структура называется ди­намически связанным списком. Разновидностью таких структур данных являются полуста­тические структуры, имеющие обычно переменный размер, не превышающий заранее определенного верхнего предела.

1.Связанные списки

Их используют для : 1) Моделирования дискретных систем 2) Арифметических операций над многочленами 3) Топологической сортировке 4) Работе с разреженными матрицами 5) Манипулировании с алгебраическими функционалами 6) Построении компиляторов и ОС 7) В СУБД

2.Линейные списки – это частный случай списка с n >= 0 узлами.

Свойства : 1.x1 – первый узел 2. Для xi, n>i>1 : xi->xi+1 3.xn –последний узел

Операции : 1. Доступ к xi для работы с ним 2. Включение/исключение нового элемента 3. Объединение списков/ разбиение на списки 4. Копирование списков 6. Сортировка/ подсчет узлов списка 7. Поиск узла

Примеры полустатических структур — очередь, стек.

Стек (магазин, список LIFO — Last In First Out) — после­довательный список переменной длины, включение и исклю­чение элементов из которого производится только с одной сто­роны.

Главные операции при работе со стеком — включение и ис­ключение элемента — осуществляются с вершины стека, при­чем в каждый момент доступен элемент, находящийся на вер­шине стека.

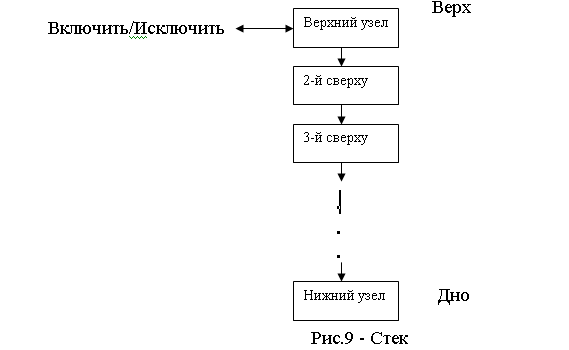
Набор процедур для работы со связанным стеком

В самом начале проги д.б.описание типов данных

Type ссылка = ^узел;

узел = record

данные: тип;

связь: ссылка

end;

Очистка

Type стек = ссылка;

Procedure очистить_стек (var s: стек);

Begin

s:= nil

End;

Включение

Type стек = ссылка;

Procedure вкл_стек (d: тип данных; var s: стек);

Var x: ссылка;

Begin

new (x);

with x^ do

begin

данные:= d;

связь:= s

end;

s:= x

End;

Исключение

Function искл_стек (var d: тип данных; var s: стек):boolean;

Var x: ссылка;

Begin

if s = nil then искл_стек:= false

else

begin

искл_стек: = true;

x:= s;

with s^ do

begin

d:= данные;

s:= связь

end;

dispose(x)

end

End;

Переменные в процедурах: s – указатель на вершину стека

x – вспомогательная ссылочная переменная

d – переменная для хранения данных из узла.

Очередь — последовательный список переменной длины, в котором включение элементов производится с одного конца списка (с хвоста), а исключение элементов — с другого (из го­ловы). Очередь работает по принципу FIFO — First In First Out.

Процедуры – исключение/включение/очистка и т.п.

Недостатки – нет доступа к предшествующим элементам списка; обязательно хранить указатель на начало и конец списка для многократного обращения к нему. Выход :

• циклический список в котором начало и конец замкнуты и вводится маркированный элемент начала списка.

• двунаправленный список – элементы такого списка содержат ссылки на родителя и потомка.

• Коралловое кольцо – двунаправленный список , в котором нечетные элементы ссылаются через один элемент, а четные на начало.

Набор процедур для работы со связанной очередью

Type ссылка = ^узел

узел = record

данные: тип данных;

связь: ссылка

end;

l,r: ссылка

end;

Очистка

Type очередь = record

Procedure очистить_очередь (var q:очередь);

Begin

q.l = nil;

q.r = nil

End;

Включение

Procedure вкл_очередь (d: тип данных; var q: очередь);

Var x: ссылка;

Begin

new (x);

if q.l = nil then q.l := x;

with x^ do

begin

данные:= d;

связь:= nil

end;

q.r^.связь:= x;

q.r:= x

End;

Исключение

Function искл_очередь (var d: тип данных; var q: очередь): boolean;

Var x: ссылка;

Begin

if q.l = nil then искл_очередь:= true

else

begin

искл_очередь:= false;

x:= q.l;

with x^ do

begin

d:= данные;

q.l:= связь

end;

dispose (x)

end

End;

Дек – очередь с двумя концами с обоих сторон

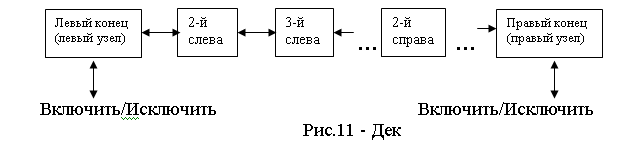
2. Кольцевые списки. Многосвязные списки, примеры применения.

Список описывается дескриптором — особой записью, со­держащей имя списка, указатель начала списка (РВ), текущее количество элементов, описание структуры элемента. Для доступа к элементу списка необходим его просмотр «с головы» — каждый раз с начала списка, что может быть медленным. Чтобы устранить этот недостаток, делают кольцевой список, т.е. указатель от последнего элемента направ­ляют на первый элемент. В таком случае просмотр списка можно начинать с любого элемента, а после доступа к нужному элементу в РВ надо занести адрес его последователя.

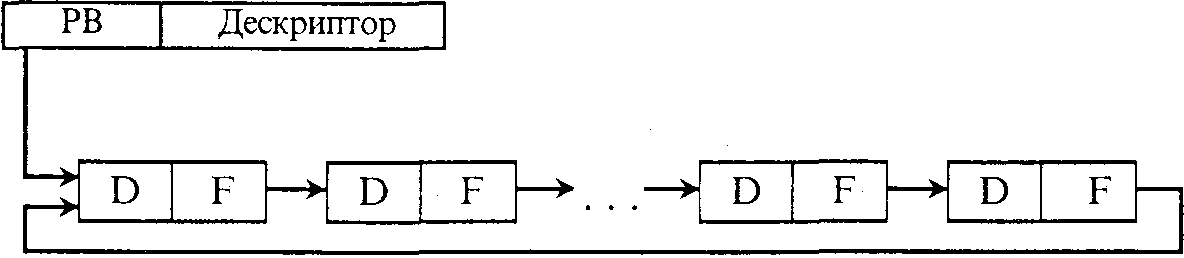
Характерные черты кольцевого списка:

1.из любого элемента списка можно достичь любого др.эл-та списка

2.цикл.список не имеет 1-го и последнего эл-та.Удобно исп-ть к.-л. Внешний указатель на последний

эл-т l(st), когда след.за ним эл-т становится первым

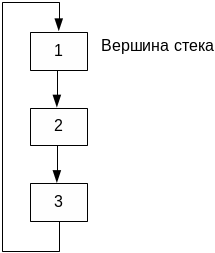
Циклический список исп-т для организации стека и очереди

1)в стеке указатель lst является ссылкой на последний элемент и явл.вершиной стека

2)для очереди:

Двунаправленный связанный список – это линейный список, в котором каждый элемент содержит два указателя: один указатель указывает на предшествующий элемент, а другой – на последний.

Двунаправленные связанные списки могут быть линейными и циклическими, могут содержать или не содержать элемент заголовка (рис. 14).

nil

nil

Рис. 14 – Двунаправленный связанный линейный список.

Рис. 15 – Двунаправленный циклический список без заголовка.

Внешний указатель

на заголовок

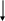
Рис. 16 – Двунаправленный циклический список с заголовком.

Главные операции со списками — вставка элемента в спи­сок и его исключение из списка. Операция вставки нового элемента в список перед задан­ным элементом для линейного односвязного списка будет вы­полняться неэффективно, т.к. в каждом элементе существует ссылка только на следующий элемент.

Используют цикл.списки: СУБД; трансляторы, компиляторы ,ОС; мат.задачи, сложение многочлена.

Пример: Использование двух связанных двунаправленных списков для представления разреженных матриц(пример многосвязных линейных списков)

Разреженная матрица – это матрица высокого порядка, в которой большинство элементов равно нулю.

Цель состоит в том, чтобы оперировать с матрицей так, будто матрица представлена в памяти вся, но для экономии не отводить место на нулевые элементы.

Рассмотрим такое представление, которое состоит из циклически связанных списков для каждой строки и каждого столбца. Каждый узел матрицы представим в виде записи, содержащей пять полей.

Влево

Индекс строки

Индекс столбца

Значение

Вверх

Влево, вверх: связи со следующим ненулевым элементом слева в строке или вверху в столбце.

14 0 0 0

10 0 13 0 - разреженная матрица

0 0 0 0

-15 0 -21 2

Связь в головах горизонтальных списков является адресом самого правого значения в строке, а связь “вверх” в головах вертикальных списков является адресом самого нижнего значения в столбце.

При последовательном распределении памяти матрица размера 200*200 заняла бы 40000 слов, в то же время разреженная матрица 200*200 с большим числом нулевых элементов может быть представлена в вышеописанной форме в ОП, содержащей приблизительно 4000 слов (в 10 раз меньше расход памяти). Разреженные матрицы применяются в алгоритмах решения линейных уравнений, обращения матриц и линейного программирования (симплекс - метод).

Многосвязные списки применяются также в базах данных

3. Древовидная структура, основные понятия. Способы обхода бинарного дерева.

Древовидная структура – это конечное множество, содержащее один или более узлов (n) такое, что:

1.имеется один специально обозначенный узел называемый корнем данного дерева.

2.остальные узлы содержатся в m>= 0 попарно непересекающихся множествах

T₁, Т₂, … , Т_m, каждое из которых в свою очередь является деревом.

3.Деревья T₁, Т₂, … , Т_m называются поддеревьями данного корня.

Дерево - это граф, который характеризуется следующими свойствами:

1. Cуществует единственный элемент (узел или вершина), на который не ссылается никакой другой элемент - и который называется корнем

2. Начиная с корня и следуя по определенной цепочке указателей, содержащихся в элементах, можно осуществить доступ к любому элементу структуры.

3. На каждый элемент, кроме корня, имеется единственная ссылка, т.е. каждый элемент адресуется единственным указателем

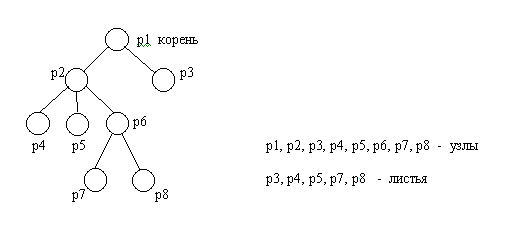
Линия связи между парой узлов дерева называется обычно ветвью. Те узлы, которые не ссылаются ни на какие другие узлы дерева, называются листьями (или терминальными вершинами) (рис. 4.1, 4.2 - b,k,l,h - листья). Узел, не являющийся листом или корнем, считается промежуточным или узлом ветвления (нетерминальной или внутренней вершиной).

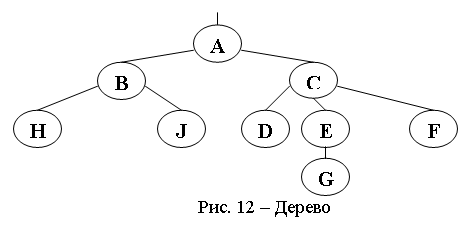
Дерево обычно изображается в перевернутом виде с корнем вверху, листьями внизу (рис. 12).

Дерево может быть определено как иерархия узлов с парными связями, в которой:

1. самый верхний уровень иерархии имеет один узел, называемый корнем;

2. все узлы, кроме корня, связываются с одним и только одним узлом на более высоком уровне по отношению к ним самим.

На самом верхнем уровне иерархии имеется только один узел – корень. Каждый узел, кроме корня, связан с одним узлом на более высоком уровне, называемым исходным узлом для данного узла. Каждый элемент может быть связан с одним или несколькими элементами на более низком уровне, которые называются порожденными.

Степень узла – число непосредственных потомков внутреннего узла.

В примере (рис. 12) степень узлов: A,B – 2, C – 3, E – 1; H,J,D,G,F – 0.

Из-за рекурсивности определения каждый узел дерева можно считать корнем некоторого поддерева. При этом число поддеревьев (порожденных узлов) данного узла называется его степенью.

Если х находится на уровне i, то говорим, что y на уровне i+1. Узел у, который находится непосредственно под узлом х называется непосредственным потомком х (или сыном, или подчинённым). Узел x называется непосредственным предком y (или исходным, или отцом). Считается, что корень дерева находится на уровне 1

Уровень узла по отношению к дереву Т определяется следующим образом:

 корень дерева имеет уровень 1;

 корни поддеревьев, непосредственно входящих в дерево, имеют уровни 2,3, и т.д.

Глубина (высота) дерева – максимальный уровень узла дерева (в примере дерево имеет глубину равную четырем) или число уровней в дереве.

Степень дерева – максимальная степень его узлов (в примере дерево имеет степень = 3, т.к. максимальная степень узла = 3).

Лист (концевой узел, терминальный элемент) – элемент не имеющий потомков – это узел степени 0. (на рис. H,J,D,G,F – листья)

Внутренний узел (или узел разветвления) – это узел, не являющийся концевым (т.е. не являющийся листом).

Момент – число узлов (в примере – 9).

Вес – число листьев (в примере – 5).

Основание – число корней. (в примере – 1)

Длина пути х – число ветвей (ребер), которые необходимо пройти, чтобы продвинутся от корня к узлу х. Корень имеет длину пути 1, его непосредственный потомок – длину пути 2 и т.д. Вообще узел на уровне i имеет длину пути i.

Длина пути дерева – сумма длин путей всех его узлов. Она так же называется длинной внутреннего пути.

Средняя длинна пути Р_i есть:

, где n_i число узлов на уровне i.

Лес – множество (обычно упорядоченное), состоящее из некоторого (может быть равного 0) числа непересекающихся деревьев.

Дерево сбалансировано, если для каждого его узла высота левого и правого поддеревьев различается не более чем на 1.

Высота сбалансированного дерева , где n – количество узлов.

1. В виде вложенных множеств:

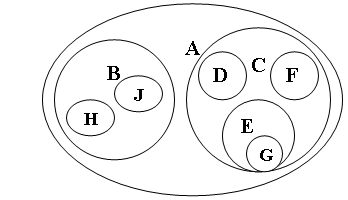
1. В виде вложенных скобок

(А(В(H)(J))(C(D)(E(G))(F)))

3. В виде ступенчатой записи

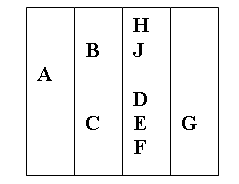
2. В виде графа:

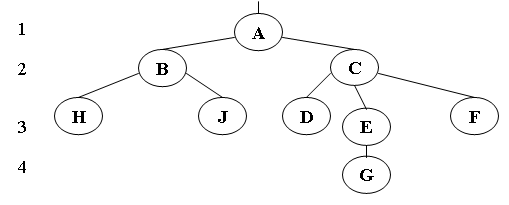
Для ориентированного графа число ребер, исходящих из некоторой начальной вершины V, называется полустепенью исхода этой вершины. Число ребер, для которых вершина V является конечной, называется полустепенью захода вершины V, а сумма полустепеней исхода и захода вершины V называется полной степенью этой вершины.

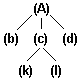
Ориентированное дерево - это такой ациклический ориентированный граф, у которого одна вершина, называемая корнем, имеет полустепень захода, равную 0, а остальные - полустепени захода, равные 1. Ориентированное дерево должно иметь, по крайней мере, одну вершину. Изолированная вершина также представляет собой ориентированное дерево.

Бинарное дерево – конечное множество узлов, которое или пусто, или состоит из корня и из двух непересекающихся бинарных деревьев, называемых левым и правым поддеревьями данного корня. Сама природа представления данных в компьютере устанавливает точный порядок для всякого дерева, и поэтому в большинстве случаев наибольший интерес представляют упорядоченные деревья.

Бинарное дерево – упорядоченное дерево степени 2.

Бинарные деревья классифицируются по нескольким признакам. Введем понятия степени узла и степени дерева. Степенью узла в дереве называется количество дуг, которое из него выходит. Степень дерева равна максимальной степени узла, входящего в дерево. Исходя из определения степени понятно, что степень узла бинарного дерева не превышает числа два. При этом листьями в дереве являются вершины, имеющие степень ноль.

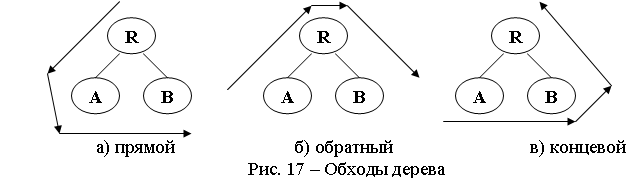
Способы обхода бинарного дерева.

Обход дерева производится в определенном порядке:

1.прямой порядок( процедура Preorder(префиксный) , рекурсивная процедура r_Preoder);

2.обратный порядок(процедура Inorder(инфиксный), рекурсивная процедура r_Inorder);

3.концевой порядок(процедура Postorder (постфиксный), рекурсивная процедура r_Postorder).

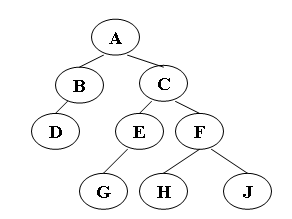
1. A B D C E G F H J – при прохождении в прямом порядке.

2. При обратном прохождении заходим в корень после того, как прошли узлы одного из поддеревьев, а затем переходим к узлам другого поддерева; при этом мы проходим узлы в таком порядке, как если бы все они были спроектированы на одну горизонтальную линию:

D B A E G C H F J

3. D B G E H J F C A – при прохождении в концевом порядке.

Эти три способа расстановки узлов бинарного дерева в последовательность чрезвычайно важны, поскольку они используются во многих методах, применимых к деревьям.

4. Дерево поиска. Включение элементов. Удаление элементов из дерева поиска.

Бинарные деревья часто используются для представления множеств данных, элементы которых имеют ключи – некоторые значения (числовые или символьные), по которым один элемент отличается от другого.

Если дерево организованно так, что для каждого узла внутри дерева все ключи в левом поддереве меньше, чем в правом, то – это дерево поиска. Используют для зщадачи сортировки и для задачи поиска

Рассмотрим пример размещения последовательности целых чисел в виде дерева поиска. Будем считать, что в последовательности могут встречаться одинаковые элементы, поэтому в узле будем хранить ключ (само число) и счетчик.

Type ссылка =^ узел;

Узел = record

Ключ : integer;

Счетчик : integer;

Лев, прав : ссылка;

End;

Процесс поиска представим в виде рекурсивной процедуры. Параметр процедуры Р передается как параметр-переменная, а не как параметр-значение. В случае включения переменной должно присваиваться новое значение ссылки, которая перед этим имела значение nil.

Алгоритм поиска по дереву с включением очень часто применяется в программах работы с базами данных (в СУБД) и в трансляторах для организации объектов, которые нужно хранить и искать в памяти.

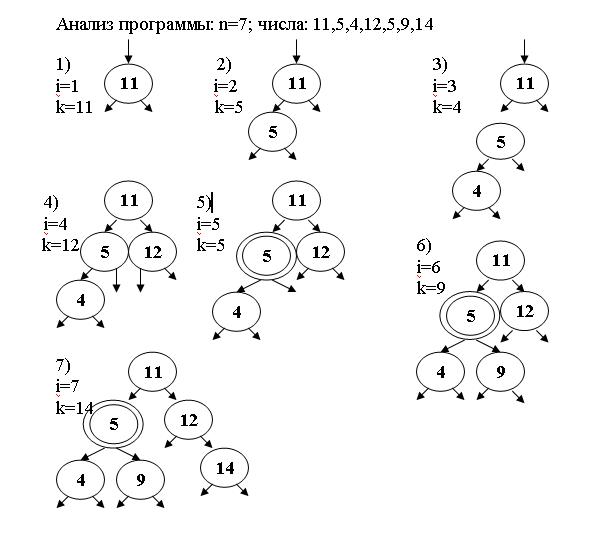
Способы обхода и поиска :

1. Попасть в корень. Попасть в левое поддерево . Попасть в правое поддерево - RAB

2. Попасть в левое поддерево Попасть в корень. Попасть в правое поддерево –ARB

3. Попасть в левое поддерево Попасть в правое поддерево Попасть в корень. – ABR

В таком случае поиск осуществляется min за n сравнений , где n – глубина дерева.

При поиске с включением, если элемент есть, то ничего не происходит, иначе – элемент порождается и возвращает на себя ссылку своему предку.

Процесс поиска представим в виде рекурсивной процедуры.

Параметр процедуры Р передается как параметр-переменная, а не как параметр-значение. В случае включения переменной должно присваиваться новое значение ссылки, которая перед этим имела значение nil.