Основы регрессионного анализа.

На практике часто встречается необходимость в установлении связей между двумя величинами y и x из которых x является переменной, но не случайной величиной, применяющей в каждой серии опытов вполне определённое значение. Величина y является случайной величиной. Потоянную дисперсию, независящую от x . которое меняется для каждого нового значения x . При регрессионного анализе тип уравнения предполагаемый должен быть известен. Если уравнение линейно, то в задачи регрессионного анализа входит:

1. Проверка однородности дисперсий.

2. Нахождение оценок-параметров a и b.

3. Определение доверительных интервалов для истинных значений коэффициентов a и b.

4. Определение критерия для проверки гипотезы о линейности регрессии y’ на x

Ломанную необходимо заменить теоретической, которая выражается Наилучшей теоритической кривой будет та, относительно которой разброс точек наблюдений y будет наименьшим. Параметры a и b такой линии определяются с помощью метода наименьших квадратов. Перед определением параметров a и b необходимо проверить гипотезу однородности дисперсии 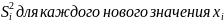. . Если гипотеза од однородности дисперсии подтверждается, то определяют параметры a и b.

Метод наименьших квадратов.

Допустим имеются некоторые переменные x, y, z. 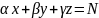Значения , , Чтобы определить неизвестные значения коэффициентов или параметров уравнения необходимо было бы найти опытным путём значение их величины при 3-х различных комбинациях переменных x,y,z. ; ; .

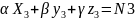Решим полученную систему уравнений можно найти . Но если теперь переменным x,y,z. X4,y4,z4 и определить опытным путём, то окажется, что при вычисленных значениях коэффициентов . Всё не будет равно N4. Это объясняется тем, что значения x4,y4,z4 носят случайный характер. Получается, что значения неизвестных надо находить в результате не 3-х математически достаточных опытов. Тогда значения коэффициентов будут достаточно надёжными. Полученная система уравнений носит название избыточной, т.к. число уравнений больше числа неизвестных. Сами же уравнения называются условными, т.к. они не вполне совместимы, т.е. значения неизвестных, определённые, например, из 1-3 уравнений системы не будут равны значениям этих же неизвестных, определённых из других 3-х уравнений. Возникает вопрос: каковы должны быть значения коэффициентов , чтобы избыттчная система удовлетворялась наилучшим образом. Где n расчётные значения, ni – экспериментальные значения.

Для решения поставленной задачи используют принцип Лежандра, согласно которого из всех возможных величин а,б,г наиболее удовлетворительными будут те, у которых сумма квадратов ошибок будет наименьшей. Для соблюдения последнего условия необходимо, чтобы сумма частных производных по обращалась в ноль, а следовательно и каждой из этих частынх производных должна обратиться в 0.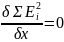 отсюда значения альфа и т.д., которые обозначают каждую из этих производных в 0, будут давать наиболее подходящее значение коэффициентов. Решая полученные уравнения в частных производных относительно альфа и т.д. получим наилучший значения коэффициентов, удовлетворяющие принципу наименьших квадратов. Если уравнениеЕсли уравнения имеет линейную зависимость, то для определения коэффициентов а и б. по методу наименьших квадратов составляется уравнение: и взяв частные производные по а и б приравниваем их к 0. E^2_i равняется два – сумма y_i + b сумма x_i + сумма a_i = 0. 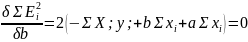решая полученную систему уравнений определяем a и b. По методу наименьших квадратов.