Системы случайных величин

Понятие о система случайных величин. До сих пор рассматривались случайные величин возможные значения которых определялись одним числом. Такие величины называют одномерными. Кроме таких величин существуют величины возможные значения которых определяются 2,3 и т.д. n числами. Такие величины называют двумерными, трёхмерными, n-мерными. Например расстояние от оси отверстия до каких-либо поверзностей деталей задётся как правило вдоль осей X и Y. В результате получаем случайную точку на плоскости с координатами X и Y, т.е., двумерную случайную величину.

Обычно этот закон распределения задаётся в виде таблицы.

Y	X
	X1	X2	X3	…	Xn
Y1	P(x1;y1)	P(x2;y1)	P(x3;y1)	…	P(xn;y1)
Yn	P(x1;y1)	P(x1;y1)	P(x1;y1)	…	P(x1;y1)

НА пересечении столбца и строки указаны вероятность 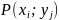; Эта вероятность показывает когда случайная величина примет значение . Т.к. события образуют полную группу, то сумма вероятностей, помещённых во всех клетках таблицы всегда равна 1. Т.о., чтобы по таблице распределения найти вероятность того, что одномерная случайная величина примет определённое значение надо просуммировать вероятности из соответствующей этому значению строки (столбца) данной таблицы. Если зафиксировать какое-то значение одной переменной, например, 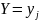, то полученное распределение случайной величины называется условным распределением при условии, что . Вероятности этого распределения будут условными вероятностями события , найденными в предположении, что событие произошло.

Основы корреляционного анализа

Общие сведения.

Статистическая проверка гипотез позволяет с помощью критериев согласия проверить правильность или неправильность выдвинутых гипотез, однако, она не отвечает на вопрос: «Какова сила и форма влияния разных факторов на исследуемый процесс?» Во многих практических задачах требуется установить и оценить зависимость изучаемой случайной величины от случайной (неслучайной) другой величины. Две случайные величины могут быть связаны:

• Функциональной зависимостью Т.е. величина Y полностью определяется значениями .

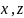• статистическая зависимость (стохастическая). Эта зависимость обычно обнаруживается при массовом изучении процесса. Например, значит между X и Y есть статистическая зависимость, т.к. есть случайные факторы . Статистическая зависимости, это когда изменение одной ведёт к изменению другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин меняется среднее значение другой. В этом случае зависимость называют корреляционной Т.о., понятие корреляционной связи является более узким, чем понятие статистической связи, т.к. среднее арифметическое является лишь одним и х параметров распределения и не определяет закон распределения в целом.

Если имеются две статистические случайные величины и если различным значениям соответствует определённые средние для , которые называют условными средними, то связь между 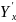и называют корреляционной связью. Корреляционная связь может быть прямолинейной и криволинейной. В общем случае уравнение вида 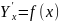называют корреляционным уравнением, а чаще – уравнением регрессии.

Ковариация и коэффициент корреляции.

Допустим, имеется двумерная случайная величина . Распределение которой задано в виде таблицы (см выше). Тогда можно найти математическое ожидание 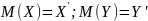, а также дисперсии одномерных составляющих 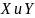. Однако математического ожидания и дисперсии может не хватить для полной характеристики двумерной случайной величины 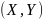. Это связано с тем, что математические ожидания дисперсии не выражают степень зависимость составляющих . Для этого вводят понятие ковариации и коэффициента корреляции. Ковариации случайных величин называют математическое ожидание, произведения отклонения этих величин от своих математических ожиданий. 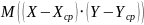Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и рассеяние этих величин вокруг точки с координатами 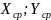. Свойства ковариации:

• ковариация двух независимых случайных величин = 0.

• Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение их ожиданий. .

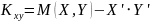• Ковариация двух случайных величин по абсолютной величине не превосходит произведение их средних квадратических отклонений.

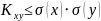
• Дисперсия суммы двух случайных величин

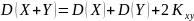
• Ковариация величина размерная её размерность определяется произведением размерности случайных величин это затрудняет использование ковариации для оценки использования случайных величин. Этого недостатка лишён коэффициент корреляции.

Коэффициентом корреляции называется отношение их ковариации к произведению средних квадратических отклонений этих величин. – безразмерная величина. Свойства коэффициента корреляции:

• Коэффициент корреляции принимает значения на отрезке от [-1;1]

• Если случайные величины независимы, то их коэффициент корреляции равен 0 или говорят, что эти случайные величины не коррелированы.

• Если коэффициент корреляции двух случайных величин равен по абсолютной величине 1, то между этими случайными величинами существует линейная функциональная зависимость.

Последовательность корреляционного анализа.

Допустим, одно и тоже значение X в процессе эксперимента (опыта, исследования) встречается раз, а одно и тоже значение 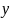в процессе опыта - 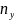раз. Одна и та же пара чисел может наблюдаться 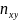раз. Все эти данные в процессе эксперимента.

Все эти данные записывают в виде таблицы.

Y	X
	10	20	30	40
0.4	5	-	7	14		26
0.6	-	2	6	4		12
0.8	3	19	-	-		22
	8	21	13	18		60

Находятся частоты. Например частота 5 указывает, что пара чисел (10; 0.4) наблюдалась 5 раз. В ячейке, расположенной в нижнем правом углу таблицы помещают сумму всех частот (общее число наблюдений).

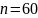
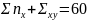
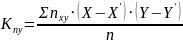
– частота появления значений x,y берётся на пересечении строки и столбца. Затем определить можно коэффициент корреляции . среднее квадратическое отклонение величин условных средних арифметических значений yx’ от общей средней y’. – число значений таблицы. Свойства корреляционного отношения: не превосходит 1. Если 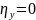, то это является необходимым и достаточным условием того, что корреляционная связь между X и Y отсутствует. Если эта величина =1, то это является необходимым и достаточным условием того, что между X и Y существует однозначная функциональная связь. 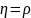то корреляционная связь между x и y строго линейная. Если на основании анализа величин и установлено налицие прямолинейное корреляционной связи между Y и X, то связь эту можно выразить следующим уравнением. 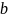– коэффициент регрессии на А само уравнение – уравнением регрессии . Поскольку, в этом уравнении величин… то в простейшем случае. . Если очень мало, то возможна криволинейная связь. Для криволинейных корреляционных связей силу связей оценивают по корреляционному отношению. Это отношение является мерой нелинейности. Чаще всего криволинейная связь описывается уравнением параболы, т.е. 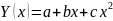коэффициенты уравнения 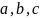определяют методом наименьших квадратов.

Оценка с помощью таблицы может быть недостаточной.

Например ро и ну могут случайно отличаться друг от друга и от нуля. Если в результате обработки опытных данных выборки получено какое-то значение коэффициента корреляции, то в связи со случайным характером этого коэффициента возникает вопрос: случайно или существенно отклонение вычисленного коэффициента от нуля. Для решения этого вопроса. Вводят значение 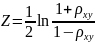. 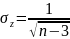Величина Z является случайной и подчиняется нормальному закону распределения со средним квадратическим отклонением , где n – объём выборки. Имеются статистические таблицы изменения z в зависимости от ро. Определяют критерий t = z/\sigma_z. Если эта величина меньше 0.05, то отклонения существенно. Это свидетельствует о наличии корреляционной связи. Если больше, то отклонение ро случайно и можно принять его равным 0. Кроме величины z и t правильность можно установить путём проверки их ошибок.

Если кажлое из этих отношений больше 4, то можно считать, что достоверность докащана.