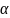Генеральная и выборочная средния
Оценка генеральной средней по выборочной
средней. Генеральной средней
 называют среднее арифметическое в
значении количественного признака
генеральной совокупности. Если все
значения x1, x2…
xn. Признака генеральной
совокупности объёмом N
различны, то
называют среднее арифметическое в
значении количественного признака
генеральной совокупности. Если все
значения x1, x2…
xn. Признака генеральной
совокупности объёмом N
различны, то
 .
Если же значения признака
.
Если же значения признака
 и т.д. имеют соответственно частоты: N1
N2 и т.д.
и т.д. имеют соответственно частоты: N1
N2 и т.д.
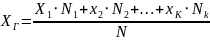 Т.о., если рассматривать исследуемый
признак, как случайную величину, то
генеральная средняя будет равна
математическому ожиданию признака.
Т.о., если рассматривать исследуемый
признак, как случайную величину, то
генеральная средняя будет равна
математическому ожиданию признака.
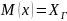 Допустим, для изучения генеральной
совокупности относительно количественного
признака
Допустим, для изучения генеральной
совокупности относительно количественного
признака
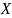 извлечена выборка объёмом n.
Отсюда даём определение: выборочной
средней Xv называют среднее
арифметическое значения признака
выборочной совокупности. Если все
значения x1, x2…
и т.д. различны, то xv
равняется (x1+x2+…xn)/n,
если значения признака имеют соответствующие
частоты, то xv будем считать
(n1x1+n2x2+…+nkxk)/n.
N1+n2+nk
= n. Т.о, выборочная средняя,
есть средняя взвешенная значения
признака, с весами равными соответствующим
частотам. Xv – всегда
какое-то конкретное число. Пусть из
генеральной совокупности в результате
независимых наблюдений над количественным
признаком X извлечено
несколько выборок. Как правило генеральная
средняя X_Г неизвестна и
требуется оценить её по данным одной
из выборок в качестве оценки генеральной
средней можно принимать выборочную
среднюю, т.е. примерно считать, что
извлечена выборка объёмом n.
Отсюда даём определение: выборочной
средней Xv называют среднее
арифметическое значения признака
выборочной совокупности. Если все
значения x1, x2…
и т.д. различны, то xv
равняется (x1+x2+…xn)/n,
если значения признака имеют соответствующие
частоты, то xv будем считать
(n1x1+n2x2+…+nkxk)/n.
N1+n2+nk
= n. Т.о, выборочная средняя,
есть средняя взвешенная значения
признака, с весами равными соответствующим
частотам. Xv – всегда
какое-то конкретное число. Пусть из
генеральной совокупности в результате
независимых наблюдений над количественным
признаком X извлечено
несколько выборок. Как правило генеральная
средняя X_Г неизвестна и
требуется оценить её по данным одной
из выборок в качестве оценки генеральной
средней можно принимать выборочную
среднюю, т.е. примерно считать, что
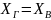 ,
можно доказать, что
,
можно доказать, что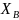 – несмещённая оценка, т.е. математическое
ожидание этой оценки равно
.
Можно также показать, что выборочная
средняя является и состоятельной оценкой
генеральной совокупности. Т.о., при
увеличении объёма выборки выборочная
средняя стремится по вероятности к
генеральной средней, а это означает,
что выборочная средняя – есть состоятельная
оценка генеральной средней. Можно также
сказать, что если по нескольким выборкам
достаточно большого объёма из одной и
той же генеральной совокупности будут
найдены выборочные средние, то они будут
приближённо равны между собой в этом
заключается свойство устойчивости
выборочных средних. Чем больше объём
выборки, тем меньше выборочное среднее
будет отличаться от генеральной средней.
– несмещённая оценка, т.е. математическое
ожидание этой оценки равно
.
Можно также показать, что выборочная
средняя является и состоятельной оценкой
генеральной совокупности. Т.о., при
увеличении объёма выборки выборочная
средняя стремится по вероятности к
генеральной средней, а это означает,
что выборочная средняя – есть состоятельная
оценка генеральной средней. Можно также
сказать, что если по нескольким выборкам
достаточно большого объёма из одной и
той же генеральной совокупности будут
найдены выборочные средние, то они будут
приближённо равны между собой в этом
заключается свойство устойчивости
выборочных средних. Чем больше объём
выборки, тем меньше выборочное среднее
будет отличаться от генеральной средней.
Для проверки нулевой гипотещы используют специально подобранную случайную величину. Точное или приближённое значение которой известно. В зависимости от вида критерия.
Статистический анализ технологических процессов
Современные технологические процессы можно рассматривать как сложные системы. На входе есть параметры, на выходе есть параметры. Есть возмущающие параметры, управляющие параметры. Поведение этой сложной системы технолог должен прогнозировать, корректировать, т.е. уметь управлять. Необходимо выявлять закономерность, влияющие на ход техпроцесса. Имеется целый ряд параметров X – входные контролируемые параметры. Y – выходные параметры. F – неконтролируемые параметры, U – контролируемые параметры. Статистические методы анализа помогают решить следующие задачи: 1. Определение соответствия точности, заданной чертёжом с действительной точностью обработки, а также точностью оборудования, оснастки и т.п.
Оценка качества настройки техпроцессов. И определение времени поднастройки.
Разработка методов контроля качества продукции.
И ряд других задач.
Методика статистического анализа точности техпроцессов заключается в последовательном выполнении ряда этапов, рассмотренных ниже:
Определение объёма выборки. От правильного определение объёма выборки зависит срок исследования, финансовые затраты, точность и надёжность результатов исследования. Условно выборки объёмом 20-30 шт. считаются малыми. При больших объёмах выборки считают большими. Для более надёжного исследования используют выборки большего объёма. Наиболее простым методом определения необходимого объёма выборки является метод с использованием таблицы достаточно больших чисел.
|
|
||||
0.1 |
… |
0.05 |
… |
0.01 |
|
0.95 |
96 |
|
384 |
|
9603 |
0.99 |
165 |
|
661 |
|
16587 |
берётся в единицах измерения исследуемого
признака или в процентах от величины
характеристики изучаемого признака.
При
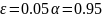 допустим в результате измерения 384 дет
получили
допустим в результате измерения 384 дет
получили
 Это означает, что истинные значения d
с надёжностью
Это означает, что истинные значения d
с надёжностью
 лежит
в приделах от 24.45- 24.55. использование
таблицы даёт несколько завышенные
результаты объёмов выборки, поэтому
таблицу используют тогда объём генеральной
совокупности
лежит
в приделах от 24.45- 24.55. использование
таблицы даёт несколько завышенные
результаты объёмов выборки, поэтому
таблицу используют тогда объём генеральной
совокупности
 выборочной совокупности, т.е. когда
выборка составляет небольшую часть
генеральной совокупности, а также в
случаях если исследование проводится
впервые или один раз. Причём ранее о тех
процессе ничего не было известно. В
общем случае объём выборки можно выбрать
с помощью формул и данных, приведённых
в технической литературе. Берётся объём
выборки
выборочной совокупности, т.е. когда
выборка составляет небольшую часть
генеральной совокупности, а также в
случаях если исследование проводится
впервые или один раз. Причём ранее о тех
процессе ничего не было известно. В
общем случае объём выборки можно выбрать
с помощью формул и данных, приведённых
в технической литературе. Берётся объём
выборки
 и
и
 .
При этом желательно иметь предварительные
данные об
.
При этом желательно иметь предварительные
данные об
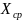 и о
и о
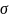 .
Полученные с помощью выборки небольшого
объёма.
.
Полученные с помощью выборки небольшого
объёма.
Оценка грубых погрешностей эксперимента. Иногда в результаты исследования вкрадываются грубые погрешности. Эти погрешности влияют на оценку точности техпроцесса и приводят к тому, что отдельные результаты наблюдений по своей величине значительно отличаются от других. Если технолог убеждён, что такие наблюдения являются результатом ошибки. Если такой убеждённости нет, то используют специальные методы обнаружения грубых погрешностей. Метод Греббса: предварительно по опытным данным выборки вычисляют характеристики распределения
 , затем определяют величину квантиля
, затем определяют величину квантиля

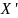 - резко выделяющиеся значение. Задавшись
процентом риска или вероятностью p=5%.
При котором грубая ошибка может быть
принята за случайную по таблицам
справочника, в зависимости от объёма
выборки находят
- резко выделяющиеся значение. Задавшись
процентом риска или вероятностью p=5%.
При котором грубая ошибка может быть
принята за случайную по таблицам
справочника, в зависимости от объёма
выборки находят
 критическое. Если
критическое. Если
 то резко выделяющееся значение
надо отбросить. После исключения грубых
ошибок из опытных данных следует снова
рассчитать выборочную среднюю и
выборочную среднюю квадратичную.
то резко выделяющееся значение
надо отбросить. После исключения грубых
ошибок из опытных данных следует снова
рассчитать выборочную среднюю и
выборочную среднюю квадратичную.Все полученные в результате измерения данные разбивают на ряд интервалом и располагают в порядке возрастания или убывания с указанием соответствующих частот или частностей. Важно правильно выбрать число интервалов. При объёме выборки n<=100
 используя последние формулы можно
составить таблицу числа интервалов.
используя последние формулы можно
составить таблицу числа интервалов.

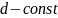 для всех интервалов. Предпочтительно
величину
для всех интервалов. Предпочтительно
величину
 выбирать из следующего ряда: 1,2,3,5,7,10,15
и далее кратно 5. Для компенсации
погрешности измерения рекомендуется
ширину интервала d
принимать ровно в два раза больше, чем
цена деления шкалы измерительного
прибора. Это условие не всегда выполнимо,
т.к. увеличении d влечёт
за собой уменьшение числа интервалов
f, а это нежелательно.
Необходимо подсчитать частоты и
частности для каждого интервала. Для
этого составляют таблицу из данных.
выбирать из следующего ряда: 1,2,3,5,7,10,15
и далее кратно 5. Для компенсации
погрешности измерения рекомендуется
ширину интервала d
принимать ровно в два раза больше, чем
цена деления шкалы измерительного
прибора. Это условие не всегда выполнимо,
т.к. увеличении d влечёт
за собой уменьшение числа интервалов
f, а это нежелательно.
Необходимо подсчитать частоты и
частности для каждого интервала. Для
этого составляют таблицу из данных.
№ интервала |
Интвервал |
Средняя величина |
Подсчёт частот |
Частота |
Частность |
Накопленная частота |
Накопленная частность |
1 |
7-12 |
9.5 |
2 |
2 |
0.02 |
2 |
0.02 |
2 |
12-17 |
14.5 |
5 |
5 |
0.05 |
7 |
0.07 |
… |
… |
… |
… |
… |
… |
… |
… |
6 |
32-37 |
34.5 |
23 |
23 |
0.23 |
61 |
0.61 |
… |
… |
… |
… |
… |
… |
… |
… |
10 |
57-62 |
59.5 |
1 |
1 |
0.01 |
100 |
1 |
Кроме таблицы, позволяющей надёжно и быстро оценить статистические характеристики строят ряд графиков для наглядности исследования. Во-первых, можно построить гистограмму и полигон частот.
Для построения кривой распределения и положения её нормы определяют среднее арифметическое X’ и дисперсию. Определяют также медиану. Для расчётов использую таблицу.
№ интервала |
Интервал |
Середина интервала |
Частота |
|
|
|
|
|
|
|
|
|
|
|
|
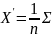
Определение закона распределения случайной величины для эффективного проведения анализа техпроцесса необходимо установить какому теоретическому закону подчиняется распределение опытных данных выборочной совокупности. Все свойства хороши изученных теоретических законов облегчая тем самым анализ явлений. Подбор соответствующего теоретического распределения осуществляется с использованием критериев согласия. Таких законов несколько. Самый распространённый – закон нормального распределения. Также можно встретить закон эксцентриситета и закон модуля разности. Нормальной распределение является чаще потому, что на тех процесс действует большое число независимых или слабо зависимых случайных причин.