
Полигон и гистрограмма
Полигоном частот называют ломанную, отрезки которой соединяют точки x1;n1 x2;n2 … xk;nk. Для построения полигона частот на оси абсцисс (х) откладывают варианты xi, а на оси ординат – соответствующие им частоты, затем точки xi;ni соединяют отрезками прямых и получают полигон частот.
Полигоном относительных частот называют ломаную отрезки которых соединяют x1; w1 x2;w2 …. Xk;wk.
xi |
1.5 |
3.5 |
5.5 |
7.5 |
wi |
0.1 |
0.2 |
0.4 |
0.3 |
При большом числе xi или непрерывном значении признака x целесообразно строить гистограмму. Для этого весь интервал значения признака x разбивают на несколько частичных интервалов (подинтервалов), длиной h. И находят для каждого частичного интервала ni, т.е. сумму частот вариант, которые попали в i интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы, длиной h, а высоты равны отношению ni/h. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь такого прямоугольника будет равна h*ni/n=hi. Площадь всей гистограммы частот равна сумме всех частот (прямоугольников и равна объёму выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h. А высоты равны wi/h – плотность относительной частоты. Для построения гистограммы относительных частот, по оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии wi/h. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. равна 1.
Статистические оценки параметров распределения.
Понятия о статистической оценке и виды оценок.
Допустим требуется изучить какое-либо
количественный признак генеральной
совокупности. Допустим, что из теоретических
соображений удалось установить, что
изучаемый признак в генеральной
совокупности распределён нормально.
Необходимо оценить параметры распределения:
математическое ожидание и среднеквадратичное
отклонение. Если бы признак подчинялся
другому закону распределения, например,
закону Пуассона, то оценить надо было
бы только один параметр
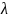 .
Обычно в распоряжении исследователя
имеются лишь данные выборки, например,
значение какого-нибудь количественного
признака: x1; x2;
x3… полученные в результате
n независимых наблюдений.
Через эти данные и надо выразить
оцениваемый параметр, рассматривая
x1,x2 и т.д.
xn, как независимые случайные
величины X1; X2….
Xn можно сказать, что найти
статистическую оценку неизвестного
параметра теоретического распределения
– это значит найти функцию от наблюдаемых
случайных величин, которая и даст
приближённые значения оцениваемого
параметра. Например, для оценки
математического ожидания нормального
распределения определяют функцию x’
= (x1+x2+… +
xn)/n, т.е.
получают среднее арифметическое
наблюдаемых значений признака. Т.о.,
статистической оценкой неизвестного
параметра теоретического распределения
называют функцию от наблюдаемых случайных
величин. Чтобы статистические оценки
давали хорошее приближение оцениваемых
параметров они должны удовлетворять
определённым требованиям. Допусти
.
Обычно в распоряжении исследователя
имеются лишь данные выборки, например,
значение какого-нибудь количественного
признака: x1; x2;
x3… полученные в результате
n независимых наблюдений.
Через эти данные и надо выразить
оцениваемый параметр, рассматривая
x1,x2 и т.д.
xn, как независимые случайные
величины X1; X2….
Xn можно сказать, что найти
статистическую оценку неизвестного
параметра теоретического распределения
– это значит найти функцию от наблюдаемых
случайных величин, которая и даст
приближённые значения оцениваемого
параметра. Например, для оценки
математического ожидания нормального
распределения определяют функцию x’
= (x1+x2+… +
xn)/n, т.е.
получают среднее арифметическое
наблюдаемых значений признака. Т.о.,
статистической оценкой неизвестного
параметра теоретического распределения
называют функцию от наблюдаемых случайных
величин. Чтобы статистические оценки
давали хорошее приближение оцениваемых
параметров они должны удовлетворять
определённым требованиям. Допусти
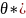 - статистическая оценка неизвестного
параметра
- статистическая оценка неизвестного
параметра
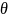 теоретического распределения. Допустим,
что по выборке объёмом n
найдена оценка
теоретического распределения. Допустим,
что по выборке объёмом n
найдена оценка
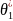 повторяя опыты многократно получим
числа
повторяя опыты многократно получим
числа
 и т.д. Оценку
и т.д. Оценку
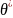 можно рассматривать как случайную
величину, а числа
можно рассматривать как случайную
величину, а числа
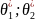 - возможные оценки. Предположим, что
оценка
даёт приближённые значения
с избытком. Это будет наблюдаться, когда
каждое найденное значения
- возможные оценки. Предположим, что
оценка
даёт приближённые значения
с избытком. Это будет наблюдаться, когда
каждое найденное значения
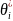 будет больше истинного значения
тогда и математическое ожидание (среднее
значение случайной величины)
будет больше
.
Если
даёт оценку с недостатком, то значение
даёт меньше, чем хотелось бы. По этой
причине естественно потребовать:
во-первых, чтобы математическое ожидание
оценки
было равно оцениваемому параметру,
т.е. мы должны потребовать, чтобы
математическое ожидание
будет равно
.
Соблюдение этого условия гарантирует
от получения систематическое ошибки.
будет больше истинного значения
тогда и математическое ожидание (среднее
значение случайной величины)
будет больше
.
Если
даёт оценку с недостатком, то значение
даёт меньше, чем хотелось бы. По этой
причине естественно потребовать:
во-первых, чтобы математическое ожидание
оценки
было равно оцениваемому параметру,
т.е. мы должны потребовать, чтобы
математическое ожидание
будет равно
.
Соблюдение этого условия гарантирует
от получения систематическое ошибки.
Несмещённой называют статистическую оценку математическое ожидание которой равно оцениваемому параметру при любом объёме выборки, т.е. всегда соблюдается это условие.
Смещённой называют такую оценку, математическое ожидание которой не равно оцениваемому параметру.
Эффективной называют оценку, которая при заданном объёме выборки имеет наименьшую возможную дисперсию. Требования состоятельности: (особенно для выборок большого объёма) состоятельной называют статистическую оценку, которая при n стремящемся к бесконечности, т.е. когда n неограниченно растёт, стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещённой оценки при n бесконечности стремится к 0, то такая оценка и будет состоятельной.
