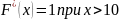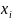Цель курса: Фундаментализация образования студентов специальности «Технология машиностроения» с целью формирования в них системного мышления, т.е. комплексного подхода к изучаемым проблемам.
Задачи: Поскольку технология машиностроения, как наука, носит в основном эмпирический характер, а не строго теоретический, требуются знания статистического подхода к решению технологических задач. В связи с широким использованием вычислительной техники(САПР) требуются знания специальных разделов математики, которые называются дискретной математикой (теория множеств, теория графов и т.д.) Для технологов проектировщиков важно не просто найти решение задачи, а лучшее ( оптимальное её решение). Отсюда необходимо знать такие разделы математики, как математическое программирование, которое позволяет решать оптимизационные задачи. Таким образом, в курсе будем заниматься математикой, носящей прикладной характер, т.е. теми разделами её, которые использует технолог в решении технологических задач.
Статистика
Элементы математической статистики.
Задачи матстата.
Матстат – раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений, массовых случайных явлений, с целью выявления существующих закономерностей. Массовыми называют явления, которые, в принципе, можно наблюдать практически неограниченное число раз. Случайным явлением называют такое, которое при неоднократном воспроизведении одного и того же опыта (эксперимента) каждый раз меняет значение.
Задачи матстата:
Указать способы сбора и группировки статистических данных, полученных в результате наблюдений или специально организованных экспериментов. (Как собирать данные).
Разработать методы анализа статистических данных, в зависимости от цели исследования. (Что делать с собранными данными). При решении второй задачи необходимо: а) Оценить неизвестную вероятность события; оценить неизвестную функцию распределения, параметры этой функции и т.д. б) Проверка статистических гипотез о виде неизвестного распределения или о величине параметров известного распределения.
Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента) и решает много других задач, например, последовательный анализ полученных статистических данных. Современную математическую статистику определяют как науку о принятии решений в условиях неопределённости.
Генеральная и выборочная совокупности. Виды выборок.
Допустим, необходимо изучить совокупность однородных объектов, относительно некоторого качественного или количественного признака, который характеризует объект. Например, имеется партия деталей, качественным признаком которой является годность деталей, а количественным – контролируемый размер детали, например, диаметр вала. Если объектов (деталей) немного, можно провести сплошное обследование, т.е. обследовать каждый объект (деталь) имеющейся совокупности. В результате получаем интересующий нас признак (какой-то размер детали), однако, сплошное обследование дорого, трудоёмко, а иногда и невозможно, так как деталей могут быть тысячи и сотни тысяч. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов (деталей) и подвергают их измерению (обследованию).
Генеральной совокупностью называется совокупность объектов, из которых производится выборка, (порой размеры генеральной совокупности сложно установить).
Выборочная совокупность (выборка) – это совокупность случайно отобранных объектов. Объёмом совокупности называют число объектов этой совокупности, иногда считают объём генеральной совокупности бесконечным, но чаще – конечным. Повторной называют выборку, при которой отобранный объект, перед отбором следующего возвращается в генеральную совокупность. Бесповторной называется выборка, при которой отобранный объект в генеральную совокупность не возвращается. На практике бесповторные выборки используют чаще.
Выборка должна правильно представлять пропорции генеральной совокупности, т.е. быть представительной. В силу закона больших чисел можно утверждать, что выборка будет репрезентативной или представительной, если её осуществлять случайно, т.е. все объекьы должны иметь одинаковую вероятность попасть в выборку.
Способы отбора объектов в выборку
Существуют различные способы отбора объектов. Принципиально их можно разбить на два вида:
Отбор не требующий расчленение генеральной совокупности на части. Сюда относят: а) Простой случайный бесповторный отбор и б) Простой случайный повторный отбор.
Отбор при котором генеральная совокупность разбивается на части. Сюда относят: а) механический отбор б) в)серийный отбор
Простым случайным называется отбор при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно по разному. Например, выписывать номера от 1 до N. На специальные карточки. Эти номера соответствуют номерам объектов. Затем наугад выбирают одну из тщательно перемешанных карточек с номером и объект, имеющий с карточкой одинаковый номер обследуется. Если при этом карточки не возвращаются имеем бесповторный отбор. Если возвращаются, то повторный отбор. При большом объёме генеральной совокупности данный способ оказывается очень трудоёмким. Для снижения трудоёмкости можно использовать таблицы «случайных чисел». Например, надо отобрать 50 объектов из пронумерованной генеральной совокупности. Открываем таблицу на любой странице и выписываем подряд 50 чисел. Затем, в выборку попадают только те объекты, номера которых совпадают с выписанными случайными числами.
Механическим называют отбор при котором генеральную совокупность чисто механически делят на столько групп, сколько объектов должно войти в выборку, а затем из каждой группы выбирают один объект. Например, если нужно отобрать 20% разработанных станком деталей, то выбирают каждую 5 деталь. Следует отметить, что иногда механический отбор может не обеспечить репрезентативность выборки. Например, если отбирают каждый 20 валик, а затем осуществляют заточку резца, то отобранными будут все валики, обработанные затупившимся инструментом. В этом случае надо менять ритм отбора и ритм заточки резца. Типический отбор. Типическим называют отбор при котором объекты выбираются не из всей генеральной совокупности, а из каждой её части. Например, если детали изготавливают на нескольких станках, то отбор производят не из всей совокупности обработанных деталей, а из деталей, обработанных на каждом станке в отдельности.
Серийным называют отбор, при котором объекты выбирают из генеральной совокупности не по одному, а сериями, а сериями, которые затем подвергают сплошному обследованию. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в исследуемых сериях незначительно ( в типическом отборе, наоборот, значительно). На практике часто используют комбинированный отбор при котором сочетаются все указанные выше способы.
Статистическое распределение выборки.
Пусть из генеральной совокупности извлечена выборка, причём
Признак
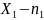 ;
;
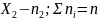 Наблюдаемые значения
Наблюдаемые значения
 называют
варианты, а последовательность
,
записанная в возрастающем порядке,
называется вариационный ряд. Числа
наблюдений
называют
варианты, а последовательность
,
записанная в возрастающем порядке,
называется вариационный ряд. Числа
наблюдений
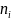 называются частотами. Их отношение к n
– относительная частота.
называются частотами. Их отношение к n
– относительная частота.
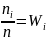 статистически распределением выборки
называют перечень вариант
и соответствующих им частот
или относительных частот
статистически распределением выборки
называют перечень вариант
и соответствующих им частот
или относительных частот
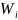 .
Иногда статистическое распределение
задают в виде последовательности
интервалов и соответствующих им частот:
.
Иногда статистическое распределение
задают в виде последовательности
интервалов и соответствующих им частот:
 .
В теории вероятностей под распределением
понимают соответствие между возможными
значениями случайной величины и их
вероятностями. А в математической
статистике – распределение – это
соответствие между наблюдаемыми
вариантами и их частотами (относительными
частотами).
.
В теории вероятностей под распределением
понимают соответствие между возможными
значениями случайной величины и их
вероятностями. А в математической
статистике – распределение – это
соответствие между наблюдаемыми
вариантами и их частотами (относительными
частотами).
Пример
Задано распределение частот в выборке n=20.
|
2 |
6 |
12 |
|
3 |
10 |
7 |

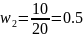

|
2 |
6 |
12 |
|
0.15 |
0.5 |
0.35 |
Эмпирическая функция распределения
Допустим, известно статистическое
распределение частот количественного
признака случайной величины X.
Например смотри пример. <Нихера не
понял.> Ну и n – объём
выборки. Тогда относительная частота
событий, когда X<x
, будет равна
 если меняется x, то меняется
и относительная частота, т.е.
– функция от x. Так как
эту функцию находят опытным путём её
называют эмпирической.
если меняется x, то меняется
и относительная частота, т.е.
– функция от x. Так как
эту функцию находят опытным путём её
называют эмпирической.
Эмпирической функцией распределения
называют функцию
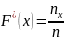 .
Эта функция определяет для каждого
значения x относительную
частоту события, когда X
будет меньше x.
.
Эта функция определяет для каждого
значения x относительную
частоту события, когда X
будет меньше x.
 – число вариант меньше x,
n – объём выборки. Чтобы
найти
– число вариант меньше x,
n – объём выборки. Чтобы
найти
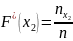 .
.
В отличие от эмпирической функции
распределения выборки, функцию
распределения генеральной совокупности
называют теоретической функцией
распределения:
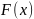 .
Различия между двумя функциями состоит
в том, что теоретическая функция F(x)
определяет вероятность события X
< x, а эмпирическая функция
.
Различия между двумя функциями состоит
в том, что теоретическая функция F(x)
определяет вероятность события X
< x, а эмпирическая функция
 определяет относительную частоту этого
же события. При увеличении n
(числа событий) до больших значений,
значения функция F*(x)
и F(x) мало
отличаются друг от друга.
определяет относительную частоту этого
же события. При увеличении n
(числа событий) до больших значений,
значения функция F*(x)
и F(x) мало
отличаются друг от друга.
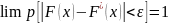 ,
где
,
где
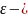 очень малая величина. Отсюда следует,
что целесообразно использовать
эмпирическую функцию распределения
для приближённого представления
теоретической функции распределения,
т.е. определив по выборке F*(x)
можно считать эту функцию равной функции
F(x) генеральной
совокупности. Такое заключение
подтверждается и тем, что свойства
функции F*(x)
совпадают со свойствами функции F(x).
Эти свойства таковы: значение эмпирической
функции распределения лежат на отрезке
от 0 до 1 и вероятность лежит в пределах
от 0 до 1. F(x)
– неубывающая функция. Если x1
наименьшая варианта, то F*(x)
=0 при x < x1.
А если x_k –
наибольшая варианта, то F*(x)=1
для всех x>x_k.
Таким образом, эмпирическая функция
распределения выборки служит для оценки
теоретической функции распределения
генеральной совокупности. Построить
эмпирическую функцию распределения по
следующим данным:
очень малая величина. Отсюда следует,
что целесообразно использовать
эмпирическую функцию распределения
для приближённого представления
теоретической функции распределения,
т.е. определив по выборке F*(x)
можно считать эту функцию равной функции
F(x) генеральной
совокупности. Такое заключение
подтверждается и тем, что свойства
функции F*(x)
совпадают со свойствами функции F(x).
Эти свойства таковы: значение эмпирической
функции распределения лежат на отрезке
от 0 до 1 и вероятность лежит в пределах
от 0 до 1. F(x)
– неубывающая функция. Если x1
наименьшая варианта, то F*(x)
=0 при x < x1.
А если x_k –
наибольшая варианта, то F*(x)=1
для всех x>x_k.
Таким образом, эмпирическая функция
распределения выборки служит для оценки
теоретической функции распределения
генеральной совокупности. Построить
эмпирическую функцию распределения по
следующим данным:
Варианты Xi |
2 |
6 |
10 |
Частоты ni |
12 |
18 |
30 |
N=60=12+18+30.
Наименьшая варианта =2, наибольшая = 10.
F*(x)=0 при