2. Разработка машинной модели системы управления скоростью
Машинная модель системы управления скоростью вращения двигателя была реализована в программном пакете MATLAB 6.5 в системе Simulink 5.0. При моделировании использовался метод Дорманда-Принца пятого порядка с фиксированным шагом интегрирования 0,002 с. Далее приводится изображение машинной модели в виде структурной схемы.
Рис. 2.1. Структурная схема системы управления скоростью
Приведём структурные схемы отдельных блоков:
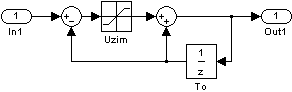
Рис. 2.2. Структурная схема задатчика интенсивности
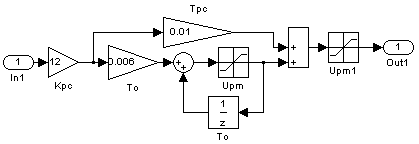
Рис. 2.3. Структурная схема регулятора скорости
Рис. 2.4. Структурная схема ЦАП
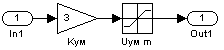
Рис. 2.5. Структурная схема усилителя мощности
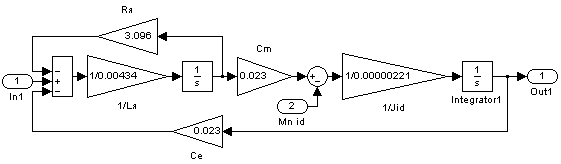
Рис. 2.6. Структурная схема исполнительного двигателя
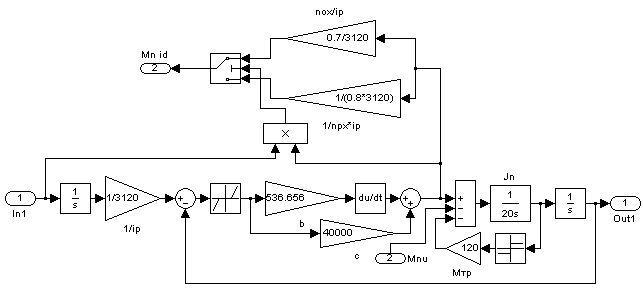
Рис. 2.7. Структурная схема редуктора и объекта управления
Рис. 2.8. Структурная схема АЦП
3. Результаты математического моделирования
В ходе математического моделирования были выбраны следующие параметры:
;
;
– период квантования;
– количество разрядов АЦП.
При данных значениях получившиеся графики переходного процесса и ошибки удовлетворяют поставленным условиям.
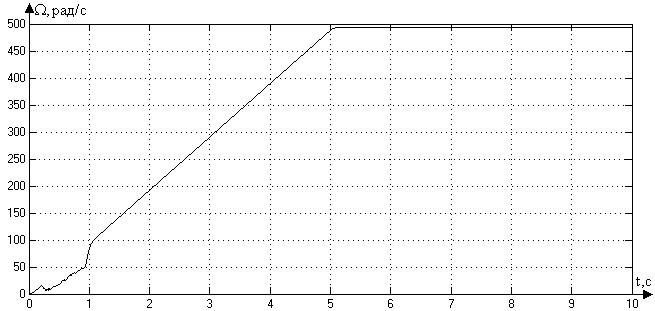
Рис.
3.1. Переходный процесс при отработке
скорости
500
Как видно из рис. 3.1. перерегулирования в системе не наступает, что удовлетворяет условиям задачи.
3.1.
Исследуем зависимость ошибки от
количества разрядов АЦП
:
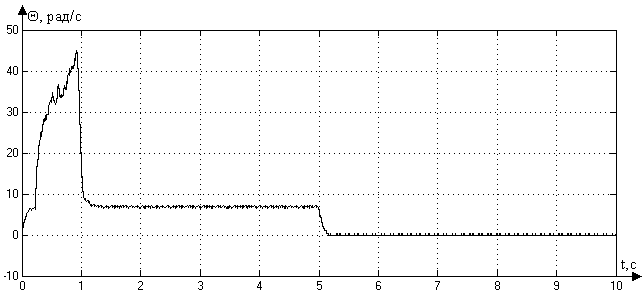
Рис. 3.2. График ошибки при отработке скорости 500 и
Величина
ошибки на участке разгона ИД равна 7
,
что не превышает заданного по условию
порога
.
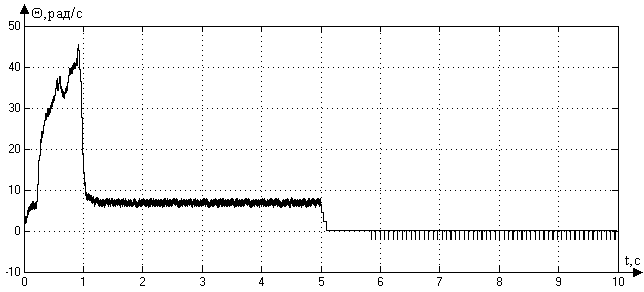
Рис.
3.3. График ошибки при числе разрядов АЦП
10
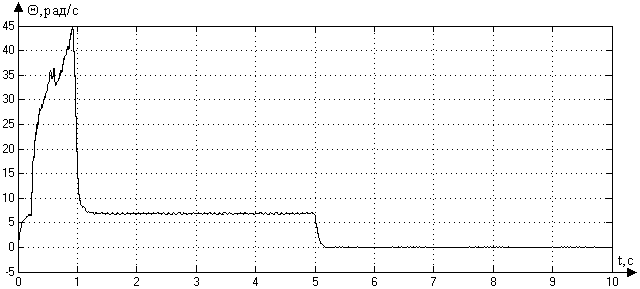
Рис. 3.4. График ошибки при числе разрядов АЦП 14
Сравнивая рис. 3.2., где дана характеристика ошибки при числе разрядов АЦП 12, и рис. 3.3., где дана характеристика ошибки при числе разрядов АЦП 10, можно заметить, что уменьшение числа разрядов АЦП ведет к увеличению ошибки на участке разгона и на участке установившегося режима.
При увеличении разрядности АЦП до 14, см. рис. 3.4., наблюдается уменьшение амплитуды колебаний ошибки на обоих участках, но на участке разгона ошибка остается неизменной и составляет 7 .
3.2. Исследуем влияние периода квантования ЭВМ на показатели качества ЭВМ.
1)
Увеличим период квантования до
:
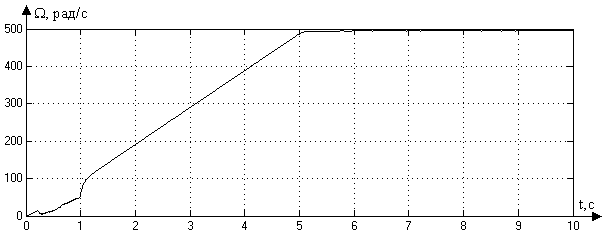
Рис. 3.4. Переходный процесс при периоде квантования
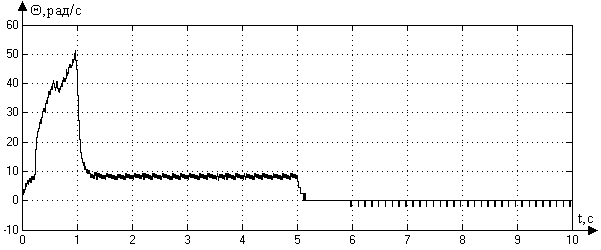
Рис. 3.5. График ошибки при периоде квантования
Сравнивая
рис. 3.2. и 3.5. видно, что при увеличении
периода квантования с
до
возрастает ошибка на участке разгона
ИД и становится практически равной
,
что недопустимо, поэтому примем решение
об уменьшении периода квантования.
2)
Уменьшим период квантования до
Рис. 3.6. Переходный процесс при периоде квантования
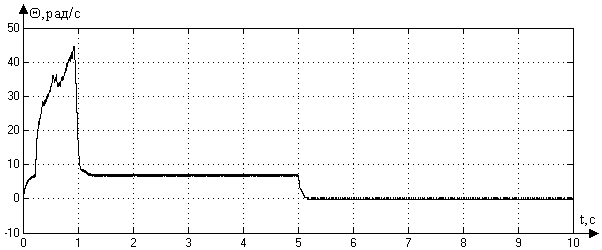
Рис. 3.7. График ошибки при периоде квантования
При уменьшении периода квантования показатели качества переходного процесса улучшается, но не значительно. Поэтому при моделировании был выбран период квантования , см. рис. 3.2., который обеспечивает заданные требования к точности системы.
