Федеральное агентство по образованию и науке

Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

Ковровская государственная технологическая академия

им. В.А. Дегтярева

Кафедра «Приборостроение»

КУРСОВАЯ РАБОТА

по дисциплине:

«Моделирование систем управления»

на тему:

«Моделирование системы управления

скоростью вращения исполнительного двигателя»

Задание 2 вариант 8

Научный руководитель: Баунин В.Г.

Исполнитель Клеветов Д.В.

Студент гр.: У - 103

2007

Содержание

Задание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1. Разработка математической модели системы управления. . . . . . . . . . 5

1.1 Математическая модель ЭВМ . . . . . . . . . . . . . . . . . . . . . 5

1.2 Математическая модель ЦАП . . . . . . . . . . . . . . . . . . . . . 6

1.3 Математическая модель усилителя мощности . . . . . . . . . . . . 6

1.4 Математическая модель исполнительного двигателя . . . . . . . . 6

1.5 Математическая модель приборного редуктора . . . . . . . . . . . 8

1.6 Математическая модель тахогенератора . . . . . . . . . . . . . . . 8

1.7 Математическая модель согласующего усилителя . . . . . . . . . . 8

1.8 Математическая модель АЦП . . . . . . . . . . . . . . . . . . . . . 8

1.9 Математическая модель редуктора и объекта управления . . . . . . 9

1.10 Математическая модель системы управления скоростью вращения

исполнительного двигателя.. . . . . . . . . . . . . . . . . . . . . . 10

2. Разработка машинной модели системы управления . . . . . . . . . . . . . 12

3. Результаты математического моделирования. . . . . . . . . . . . . . . . . 14

Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

25.04.07

У

Задание

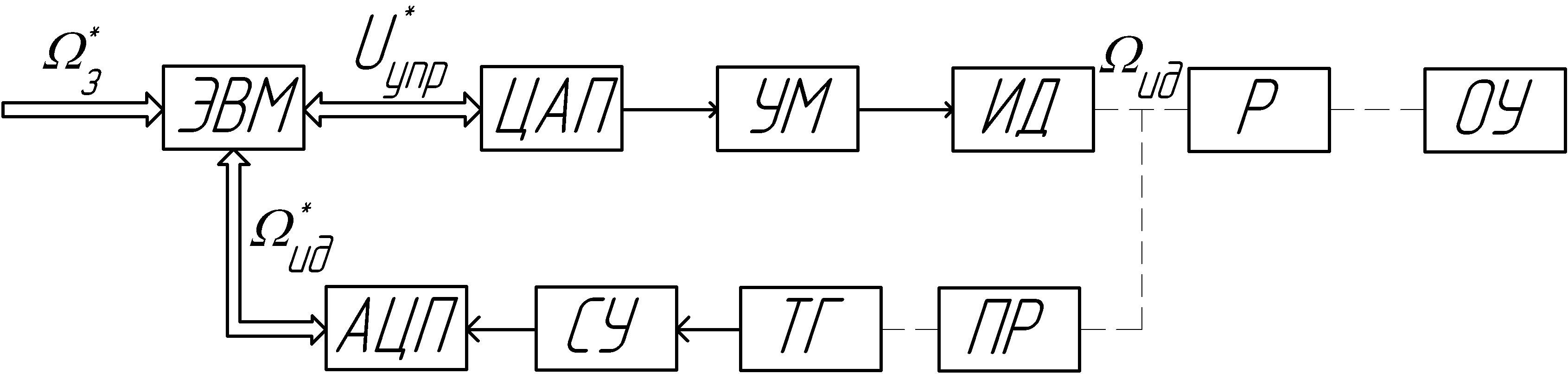
Рис. 1. Функциональная схема

Рис. 2. Алгоритм работы ЭВМ

Параметры системы:

– число разрядов ЦАП;

– максимальное выходное напряжение ЦАП;

– максимальное входное напряжение АЦП;

– крутизна тахогенератора.

Характеристики задающего воздействия:

– входной сигнал (скорость);

– скорость изменения входного сигнала (ускорение).

Параметры усилителя мощности (УМ):

– коэффициент усиления;

– максимальное выходное напряжение.

Параметры исполнительного двигателя (ИД):

– в качестве исполнительного двигателя используется электродвигатель постоянного тока с независимым возбуждением;

– номинальное напряжение якоря;

– номинальный ток якоря;

– номинальная скорость вращения;

– номинальный момент на валу;

– момент инерции ротора.

Параметры редуктора (Р):

– передаточное отношение;

– коэффициент, учитывающий момент инерции вращающихся частей редуктора;

– КПД прямого хода;

– КПД обратного хода;

– люфт;

– жесткость.

Параметры приборного редуктора (ПР):

– приборный редуктор считать абсолютно жестким и безлюфтовым;

– передаточное отношение.

Параметры объекта управления (ОУ):

– момент инерции нагрузки;

– момент сухого трения;

– момент неуравновешенности нагрузки.

Определить:

1. Значение , , периода квантования ЭВМ, число разрядов АЦП (10, 12, 14), при которых обеспечиваются следующие характеристики:

– перерегулирование при отработке входного воздействия не более 15%;

– установившаяся ошибка на участке разгона ИД при входном воздействии не более .

2. Исследовать влияние периода квантования ЭВМ на показатели качества переходного процесса.

1. Разработка математической модели системы управления скоростью вращения исполнительного двигателя

1.1. Математическая модель эвм.

Рис. 1.1. Структурная схема ЭВМ.

1.1.1. Уровень ограничения скорости изменения выходного сигнала задатчика интенсивности:

,

где – заданное ускорение;

– период квантования по времени, подбирается экспериментально.

1.1.2. Задаём диапазон изменения управляемой величины (скорость вращения ИД):

,

где – номинальная скорость вращения двигателя.

1.1.3. Выбираем количество разрядов ЭВМ:

.

1.1.4. Определяем величину младшего разряда ЭВМ:

,

где – максимальная скорость вращения двигателя.

1.1.5. Определяем уровень ограничения сигнала управления:

,

где – максимальное выходное напряжение ЦАП;

– крутизна ЦАП.

Значения и определяются в ходе исследования системы регулирования.

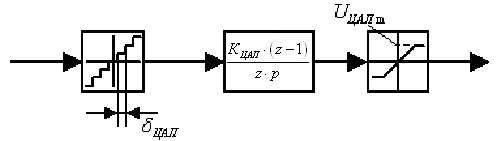
1.2. Математическая модель цап.

Рис. 1.2. Структурная схема ЦАП

Определим крутизну ЦАП:

,

где – максимальное выходное напряжение ЦАП;

– максимальная скорость вращения двигателя.

Определим величину младшего разряда ЦАП:

,

где – величина младшего разряда ЭВМ;

– количество разрядов ЭВМ;

– количество разрядов ЦАП.

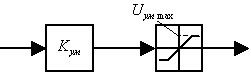
1.3. Математическая модель усилителя мощности.

Рис. 1.3. Структурная схема усилителя мощности

– коэффициент усиления;

– максимальное выходное напряжение усилителя мощности.