
- •Произвольная плоская система сил
- •1. Основные понятия и определения статики
- •2. Связи и их реакции
- •3. Уравнения равновесия плоской системы сил
- •Проекция силы на ось
- •Момент силы относительно точки
- •Основные свойства момента силы относительно точки
- •Равновесие конструкции
- •6. Приложение методов статики к расчету фермы
- •Определение опорных реакций
- •Определение усилий в стержнях фермы
- •Метод вырезания узлов
- •Метод сечения (метод Риттера)
- •Варианты индивидуальных заданий Задача 1. Определение реакций опор жесткой рамы
- •Задача 2. Определение реакций опор составной конструкции (система двух тел)
- •Задача 3. Расчет фермы
- •Литература
3. Уравнения равновесия плоской системы сил
Теорема (основная
для плоской системы сил):
Свободное абсолютно твердое тело под
действием плоской системы сил
![]() будет
находиться в покое тогда и только тогда,
когда выполняется одна из форм условий
равновесия:
будет
находиться в покое тогда и только тогда,
когда выполняется одна из форм условий
равновесия:
I
ф)
 II
ф)
II
ф)
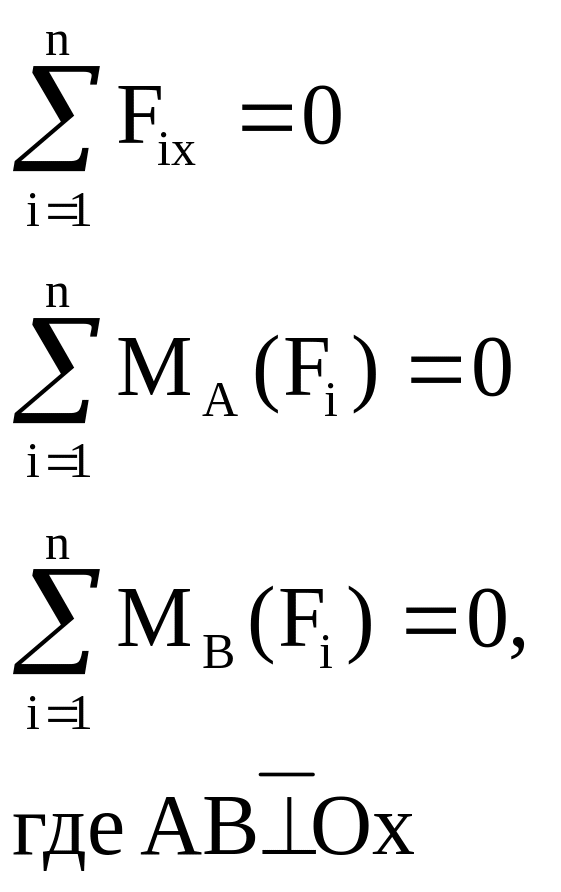 III
ф)
III
ф)

Для составления этих уравнений равновесия надо уметь находить проекцию силы на ось и момент силы относительно точки.
Проекция силы на ось
Проекция силы на ось равна взятому со знаком плюс или минус произведению модуля вектора силы на косинус острого угла между силой и осью.
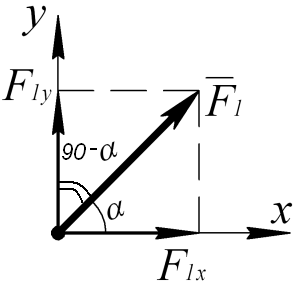
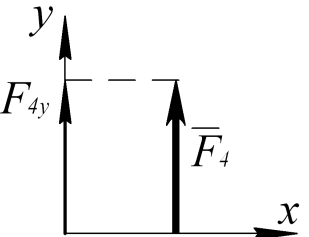
Знак плюс ставится, если сила и ось направлены в одну сторону, минус если в разные (рис.4, 5). Проекция силы на ось равна нулю, если линия действия силы перпендикулярна оси (рис.6).
![]()
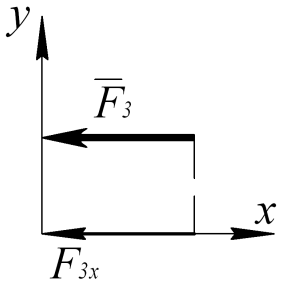 Рис.4
Рис.4
![]()
![]()
Рис.5 Рис.6
Момент силы относительно точки
Действие силы на закрепленное в одной точке тело заключается в стремлении повернуть его вокруг данной точки. В случае плоской системы сил для характеристики вращательного действия силы вводится алгебраический момент силы относительно точки, который в дальнейшем будем называть просто моментом силы относительно точки.
Момент силы относительно точки равен взятому со знаком плюс или минус произведению модуля силы на плечо.
Плечом силы называется отрезок перпендикуляра, опущенного из точки на линию действия силы.
![]()
Знак плюс, если сила вращает тело против хода часовой стрелки (рис.7) .
Знак минус, если сила вращает тело по ходу часовой стрелки (рис.8).
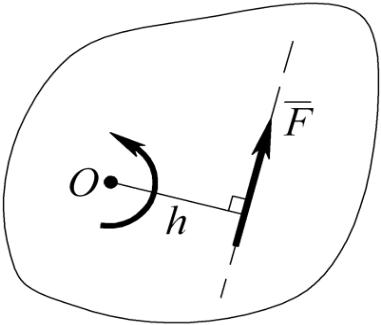
![]()
![]()
Рис. 7 Рис. 8
Основные свойства момента силы относительно точки
Момент силы относительно точки равен нулю, если линия её действия проходит через точку (
 )
( рис.9).
)
( рис.9).
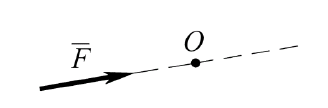
Рис.9
Теорема Вариньона: Момент суммы сил относительно точки равен сумме моментов этих сил относительно этой же точки:
![]()
Замечание: теоремой Вариньона удобно пользоваться в случаях, когда найти плечо силы затруднительно. Тогда можно силу разложить на взаимно перпендикулярные составляющие (относительно которых плечо находится просто) и воспользоваться теоремой Вариньона.
Пример: найти момент силы F относительно точки O (рис.10).
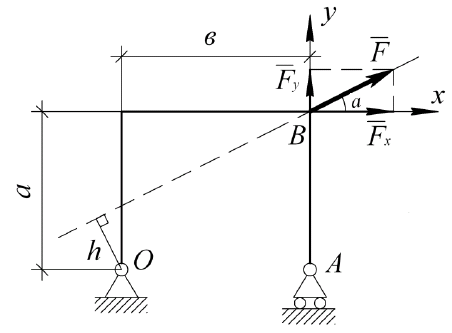
Рис.10
В данном случае найти плечо h достаточно сложно, поэтому разложим силу F на составляющие Fx , Fy (где Fx=Fcosα, Fy =Fsinα) , для которых вычислить момент относительно точки не представляется сложным:
![]() ,
,
![]() ,
,
тогда, по теореме Вариньона:
![]()
Схема решения задач статики
В статике при решении задач рекомендуется следовать следующей схеме:
1. Выявить объект (тело, точку), равновесие которого следует рассматривать.
2. Определить связи (опоры), непосредственно наложенные на тело и освободить тело от связей, заменив их действие реакциями.
3. Выявив число неизвестных в задаче, установить её статическую определимость.
4. Выбрать оси координат и составить уравнения равновесия тела под действием всех сил.
5. Решить эти уравнения относительно тех неизвестных, которые требуется определить.
6. Сделать проверку, составив дополнительные независимые уравнения.
