154 Законы распределения случайных величин [гл. 7

гипотезу следует отбросить как неправдоподобную. Напротив, если вероятность р сравнительно велика, можно признать расхождения меж­ду теоретическим и статистическим распределениями несущественными и отнести их за счет случайных причин. Гипотезу Н о том, что величина X распределена по закону F (х), можно считать правдо­подобной или, по крайней мере, не противоречащей опытным данным.

Таким образом, схема применения критерия у_² к оценке согласо­ванности теоретического и статистического распределений сводится к следующему:

1. Определяется мера расхождения у? по формуле (7.6.4).

2. Определяется число степеней свободы г как число разрядов к минус число наложенных связей s:

r = k — s.

3) По г и х^{2 с} помощью табл. 4 определяется вероятность того, что величина, имеющая распределение у² с г степенями свободы, пре­ взойдет данное значение у². Если эта вероятность весьма мала, гипо­ теза отбрасывается как неправдоподобная. Если эта вероятность относительно велика, гипотезу можно признать не противоречащей опытным данным.

Насколько мала должна быть вероятность р для того, чтобы от­бросить или пересмотреть гипотезу, — вопрос неопределенный; он не может быть решен из математических соображений, так же как и вопрос о том, насколько мала должна быть вероятность события для того, чтобы считать его практически невозможным. На практике, если р оказывается меньшим чем 0,1, рекомендуется проверить экспе­римент, если возможно — повторить его и в случае, если заметные расхождения снова появятся, пытаться искать более подходящий для описания статистических данных закон распределения.

Следует особо отметить, что с помощью критерия х² (^или любого другого критерия согласия) можно только в некоторых случаях опро­вергнуть выбранную гипотезу Н и отбросить ее как явно несо­гласную с опытными данными; если же вероятность р велика, то этот факт сам по себе ни в коем случае не может считаться доказатель­ством справедливости гипотезы Н, а указывает только на то, что гипотеза не противоречит опытным данным.

С первого взгляда может показаться, что чем больше вероят­ность р, тем лучше согласованность теоретического и статистиче­ского распределений и тем более обоснованным следует считать выбор функции F(x) в качестве закона распределения случайной величины. В действительности это не так. Допустим, например, что, оценивая согласие теоретического и статистического распределений по критерию х², мы получили р = 0,99. Это значит, что с вероятно­стью 0,99 за счет чисто случайных причин при данном числе опытов

7.61

КРИТЕРИИ СОГЛАСИЯ

155

должны были получиться расхождения большие, чем наблюденные. Мы же получили относительно весьма малые расхождения, которые слишком малы для того, чтобы признать их правдоподобными. Разум­нее признать, что столь близкое совпадение теоретического и стати­стического распределений не является случайным и может быть объяснено определенными причинами, связанными с регистрацией и обработкой опытных данных (в частности, с весьма распространенной на практике «подчисткой» опытных данных, когда некоторые резуль­таты произвольно отбрасываются или несколько изменяются).

Разумеется, все эти соображения применимы только в тех слу­чаях, когда количество опытов п достаточно велико (порядка несколь­ких сотен) и когда имеет смысл применять сам критерий, осно­ванный на предельном распределении меры расхождения при п—>оо. Заметим, что при пользовании критерием у} достаточно большим должно быть не только общее число опытов п, но и числа наблюдений т₁ в отдельных разрядах. На практике рекомендуется иметь в каждом разряде не менее 5—10 наблюдений. Если числа наблюдений в от­дельных разрядах очень малы (порядка 1 — 2), имеет смысл объеди­нить некоторые разряды.

Пример 1. Проверить согласованность теоретического и статистического распределений для примера 1 п° 7.5 (стр. 137, 146).

Решение. Пользуясь теоретическим нормальным законом распределе­ния с параметрами

т = 0,168, а = 1,448,

находим вероятности попадания в разряды по формуле

*.<ь1 *1 — т

\

Pi

где Х[, xi₊₁ — границы г-го разряда.

Затем составляем сравнительную таблицу чисел попаданий в разряды rrt[ и соответствующих значений npi (п = 500).

//	-4; -3	-3; -2	-2; -1	-1;0	0; 1	1; 2	2; 3	3; 4
пц	6	25	72	133	120	88	46	10
npi	6,2	26,2	71,2	122,2	131,8	90,5	38,2	10,5

По формуле (7.6.4) определяем значение меры расхождения

g

Определяем число степеней свободы как число разрядов минус число наложенных связей s (в данном случае s = 3):

г = 8 — 3 = 5.

156

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

[ГЛ. 7

По табл. 4 приложения находим для г = 5:

при х² = 3,00 р = 0,70; при х² = 4,35 р = 0,50.

Следовательно, искомая вероятность р при х² = 3,94 приближенно равна 0,56. Эта вероятность малой не является; поэтому гипотезу о том, что ве­личина X распределена по нормальному закону, можно считать правдоподобной.

Пример 2. Проверить согласованность теоретического и статистиче­ского распределений для условий примера 2 п° 7.5 (стр. 149).

Решение. Значения pi вычисляем как вероятности попадания на участки (20; 30), (30; 40) и т. д. для случайной величины, распределенной по закону равномерной плотности на отрезке (23,6; 96,9). Составляем сравнительную таблицу значений mi и npi (п. = 400):

h	20; 30	30; 40	40; 50	50; 60	60; 70	70; 80	80; 90	90; 100
mi	21	72	66	38	51	56	64	32
"Pi	34,9	54,6	54,6	54,6	54,6	54,6	54,6	38,0

По формуле (7.6.4) находим х²:

Число степеней свободы:

г = 8 — 3 = 5. По табл. 4 приложения имеем:

при х² = 20,5 и г = 5 р = 0,001,

Следовательно, наблюденное нами расхождение между теоретическим и статистическим распределениями могло бы за счет чисто случайных причин появиться лишь с вероятностью р я 0,001. Так как эта вероятность очень мала, следует признать экспериментальные данные противоречащими гипотезе о том, что величина X распределена по закону равномерной плотности.

К роме критерия /², для оценки степени согласованности теорети­ческого и статистического распределений на практике применяется еще ряд других критериев. Из них мы вкратце остановимся на кри­терии А. Н. Колмогорова.

В качестве меры расхождения между теоретическим и статисти­ ческим распределениями А. Н. Колмогоров рассматривает максималь­ ное значение модуля разности между статистической функцией рас­ пределения F* (х) и соответствующей теоретической функцией рас­ пределения: _п _

Основанием для выбора в качестве меры расхождения величины D является простота ее вычисления. Вместе с тем она имеет достаточно

простой закон распределения. А. Н. Колмогоров доказал, что, какова бы ни была функция распределения F (х) непрерывной случайной ве­личины X, при неограниченном возрастании числа независимых на-

Ллтппрний п прппятнпгть HenaRpHCTRa

стремится к пределу

Значения вероятности Р(Х), подсчитанные по формуле (7.6.5), приведены в таблице 7.6.1.

	Р(\)		PW		Р(Ц
0,0	1,000	0,7	0,711	1,4	0,040
од	1,000	0,8	0,544	1,5	0,022
0,2	1,000	0,9	0,393	1,6	0,012
0,3	1,000	1,0	0,270	1,7	0,006
0,4	0,997	1,1	0,178	1,8	0,003
0,5	0,964	1,2	0,112	1,9	0,002
0,6	0,864	1,3	0,068	2,0	0,001

С хема применения критерия А. Н. Колмогорова следующая: строят­ся статистическая функция распределения F*(x) и предполагаемая

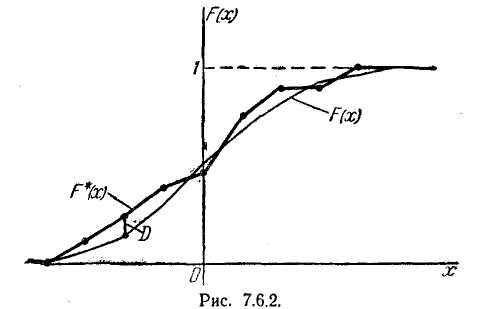
теоретическая функция распределения F(x), и определяется макси­мум D модуля разности между ними (рис. 7.6.2). Далее, определяется величина

l = DYn