
Лабораторная работа № 5
Исследование ачх и фчх простейших цепей
Цель работы: Исследовать амплитудно-частотные и фазо-частотные характеристики простейших пассивных и активных RLC-цепей, овладеть техникой измерения этих характеристик.
Подготовка к работе.
Ознакомиться с рабочим заданием и методическими указаниями к работе. Ответить на следующие вопросы:
Приведите определения частотного коэффициента передачи, амплитудно-частотной и фазовой характеристик четырехполюсной цепи.
Функция, описывающая зависимость двух любых комплексных амплитуд (токов или напряжений), называется частотным коэффициентом передачи К(jω), которая может быть представлена в показательной форме:
![]()
где К(jω) - амплитудно-частотная характеристика цепи (АЧХ),
φK(ω) - фазовая характеристика цепи (ФЧХ).
Что такое диаграмма Найквиста?
Способ графического представления частотных свойств цепей –диаграмма Найквиста. Она представляет собой годограф конца вектора К(jω) на комплексной плоскости при различных значениях частоты ω, которая изменяется в пределах от 0 до ∞.
Дайте определение характеристических сопротивлений четырехполюсной цепи и как их определить практически.
Характеристические сопротивления Z01, Z02 – это взаимосвязанная пара сопротивлений для заданной цепи. В случае если цепь нагружена, например, на выходное сопротивление Z02 по выходу, то ее входное сопротивление по входу равно Z01 (см. рис. 5.2 – прямое включение). Аналогично, если в цепи поменять входные и выходные пары полюсов местами, то при нагрузке Z01, входное сопротивление цепи будет равно Z02 (см. рис. 5.3 – обратное включение), но такое соотношение будет выполняться только для взаимной линейной цепи.
Как определяется полоса пропускания четырехполюсной цепи?
Для каких цепей существует взаимосвязь между АЧХ и ФЧХ? Приведите обоснование.
Как расчетным путем на переменном токе можно получить АЧХ и ФЧХ цепи между двумя произвольными парами зажимов цепи.
Методические сведения и указания.
Функция, описывающая зависимость двух любых комплексных амплитуд (токов или напряжений), называется частотным коэффициентом передачи К(jω), которая может быть представлена в показательной форме:
где К(jω) - амплитудно-частотная характеристика цепи (АЧХ),
φK(ω) - фазовая характеристика цепи (ФЧХ).
В теории цепей получил распространение еще один способ графического представления частотных свойств цепей – так называемая диаграмма Найквиста. Она представляет собой годограф конца вектора К(jω) на комплексной плоскости при различных значениях частоты ω, которая изменяется в пределах от 0 до ∞.
Для измерения АЧХ удобно пользоваться логарифмическими единицами – децибелами. При этом вводится понятие усиление (затухание цепи).
![]() ,
Дб
,
Дб
Если использовать отношение выходной мощности на некоторой паре полюсов цепи к выходной на другой паре плюсов то получим K(jω)2. Тогда:
![]() ,
Дб
,
Дб
Если поменять входные и выходные пары полюсов местами, то получим К(jω)обр. Когда цепь симметрична, то К(jω)= К(jω)обр.
Коэффициент передачи цепи зависит от сопротивлений генератора и нагрузки, что в свою очередь обусловлено входным и выходным сопротивлением цепи. Однозначность в определении К(jω) наступает тогда, когда сопротивление генератора и нагрузки равны характеристическим сопротивлениям. Сопротивление генератора, в этом случае, должно быть равно характеристическому входному сопротивлению цепи Z01, а сопротивление нагрузки характеристическому выходному сопротивлению цепи Z02. При этом достигается максимальный коэффициент передачи мощности от генератора через цепь в нагрузку.
Характеристические сопротивления Z01, Z02 – это взаимосвязанная пара сопротивлений для заданной цепи. В случае если цепь нагружена, например, на выходное сопротивление Z02 по выходу, то ее входное сопротивление по входу равно Z01 (см. рис. 5.2 – прямое включение). Аналогично, если в цепи поменять входные и выходные пары полюсов местами, то при нагрузке Z01, входное сопротивление цепи будет равно Z02 (см. рис. 5.3 – обратное включение), но такое соотношение будет выполняться только для взаимной линейной цепи.
Z01 Z02 Z02 Z01

 1 2
2 1
1 2
2 1








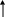
ЕГ Z02 EГ
 UВХ
UВЫХ
UВХ
UВЫХ
UВХ
UВЫХ
UВХ
UВЫХ

1’ 2’ 2’ 1’
Прямое включение Обратное включение
Рис.5.2 Рис.5.3
Для каждой линейной взаимной цепи, характеристическое сопротивления определяются с использованием «А»-параметров этой цепи:
![]()
![]()
«А»-параметры цепи можно получить с использованием Z матрицы цепи, сформированной для цепи без источника сигнала и нагрузки:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Где: - определитель матрицы Z; ij – i,j алгебраическое дополнение матрицы Z;
11 22 – сложное дополнение:
![]()
В рамках данной лабораторной работы предполагается исследовать простейшие цепи, изображенные на рис. 5.1.
В качестве подготовки к лабораторной работе рекомендуется вывести известным способом выражения для АЧХ и ФЧХ коэффициента передачи по напряжению схем, представленных на рис.5.1. При этом предположить, что в указанных схемах на входе подключен источник идеального напряжения, а по выходу схем обеспечен холостой ход. Окончательные выражения для АЧХ и ФЧХ приводим в качестве справки
для рис.5.1 г):
![]()
![]()
где W – безразмерная величина W = ωR1С; m = R1 / R2
для рис. 5.1д):
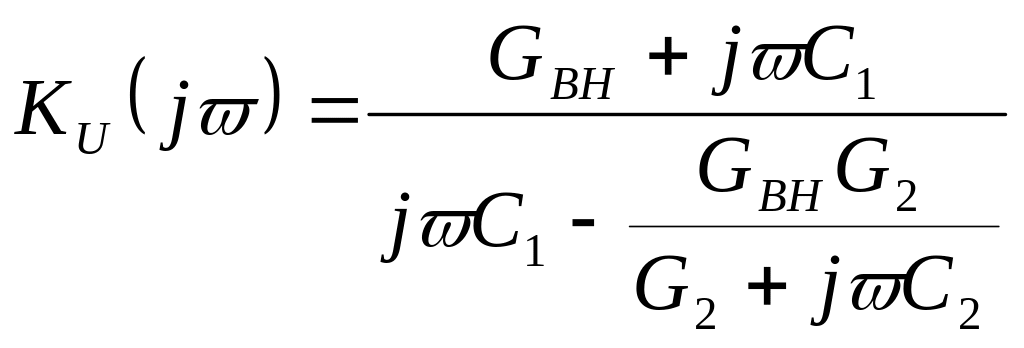
![]() где
GВН=1/RВН
где
GВН=1/RВН
В этих выражениях - круговая частота.
C







R1


Ůвх R2 Ůвых


Рис. 5.1г)
C1 3







1 R2 2

 JН=U2/RВН
JН=U2/RВН

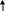 RВН
Ůвых
RВН
Ůвых
Ůвх RВХ U2 C2

Рис. 5.1д)
