11.5 Необходимое число измерений
В соответствии с приведенными выражениями для расчета доверительного интервала можно придти к выводу, что случайные погрешности результатов многократных измерений оцениваются зависимостью (для среднего арифметического значения):
Отсюда следует, что для увеличения точности можно использовать два пути:
уменьшать σX, что можно обеспечить путем использования более точного прибора;
увеличить число измерений п.
Допустим, что использовать более точный прибор невозможно. В таком случае возникает вопрос - сколько измерений необходимо, чтобы при заданной доверительной вероятности α = 0,95 доверительный интервал δХ был существенно меньше систематической погрешности δ, т.е. при заданной доверительной вероятности (требуется найти такое п, чтобы δХ<<δ. Обычно
11.6 Ошибки косвенных измерений
В большинстве случаев измеряется интересующая нас величина не непосредственно, а косвенно, путем измерения одной или нескольких величин, от которых зависит искомая величина. Например, при измерении площади прямоугольника приходится измерять его длину а и ширину b, а площадь вычисляют по формуле F = ab.
При таких измерениях, называемых косвенными, существуют свои правила в определении ошибок.
Общие правила вычисления ошибок косвенных измерений выводятся с помощью дифференциального исчисления.
Пусть результат Yкосвенных измерений зависит от результатов прямых измерений Х1,Х2,...,Хп следующим образом
F = f(X1,X2,...,Xn). (2.1)
Пусть относительные погрешности
физических величин Х1,Х2,…,Хnизвестны
и соответственно равны
Тогда
погрешность 
измерения
физической величины Y
можно найти следующим образом.
Прологарифмируем уравнение (2.1):
lnY = ln[F(X1, X2, …, Xn)] (2.2)
Вычислим полные дифференциалы правой и левой части уравнения (2.2):
(2.3)
Заменив дифференциалы конечными разностями, получим
(2.4)
Если умножить обе части уравнения (2.4) на исходные функционалы y=f(X1,...,Xn), то получим выражение для определения абсолютной погрешности косвенной величины:
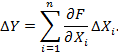
Расчет по приведенным формулам дает завышенный результат погрешностей, поскольку последние определяются путем суммирования погрешностей определения прямо измеряемых величин (без учета их знака). Реальные погрешности прямых измерений накладываются друг на друга и, в некоторой степени, взаимно компенсируются.
Из теории погрешностей известно, что более объективной оценкой результатов измерений является использование среднеквадратичной погрешности
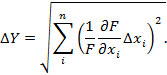
Кроме того, установлено, что приведенная зависимость определения абсолютной погрешности косвенного измерения не изменяет своего вида,если вместо ∆Yиспользовать σY, а вместо ∆Xi, использовать с σXi:
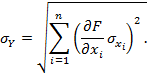
12. Математическое планирование эксперимента
В 20-е гг. XX в. английский статистик Рональд Фишер впервые предложил проводить эксперимент, варьируя одновременно всеми параметрами сразу, в отличие классического однофакторного эксперимента, в котором все параметры, определяющие состояние объекта, за исключением одного, фиксируются на определенном уровне, и в опытах изменяется только варьируемый параметр. Это событие принято считать началом использования математического планирования эксперимента
Математическое планирование эксперимента имеет своей целью повышение эффективности экспериментальных исследований, которая, по данным Дж. Бернала, составляет всего около 2 %.
В 50-х гг. американские ученые Бокс и Уилсон развивают новое направление планирования эксперимента - ортогональное планирование оптимального эксперимента. Сущность предложенного ими метода заключается в следующем. На первом этапе для некоторой локальной области существования изучаемого объекта методом планирования эксперимента определяются закономерности его поведения и в результате их анализа определяется направление к оптимуму, в котором следует изменять параметры. Далее проводят очередной эксперимент в новой области существования объекта и т.д. до тех пор, пока не будут достигнуты оптимальные условия.