11.3 Вероятностные оценки ошибок измерений

Абсолютная и относительная погрешности характеризуют единичное измерение. С целью уменьшения случайной погрешности измерение проводят многократно и используют вероятностно-статистические оценки погрешности.

При измерении любой величины X, истинное значение которой Х₀|теоретически можно получить бесконечно большой набор измеренных значений X₁,X₂,…,X_N,.... Этот набор называют генеральной совокупностью.

Обозначим абсолютную погрешность каждого измерения ∆Х_i= X_i - Х₀ . Если среднее арифметическое значение ∆Х_i, для генеральной совокупности равно 0, т.е. , то такие погрешности называют случайными.

Вероятность их появления тем больше, чем меньше их значение |∆x_i|.Кроме того, при этом существует равная вероятность появления отрицательных и положительных значений погрешности.

В большинстве случаев плотность вероятности появления случайной погрешности подчиняется нормальному закону распределения (закону Гаусса):

где Р(∆Х) – плотность вероятности появления случайной погрешности ∆Х; σ² – дисперсия.

Для генеральной совокупности среднее арифметическое X(математическое ожидание) равно истинному значению Х₀измеряемой величины X:

Степень рассеяния измеренных значений X_i вблизи Х₀ характеризуется дисперсией d(x):

,

Где σ_X – среднее квадратичное отклонение; п– 1 – число степеней свободы.

11.4 Статистическая обработка результатов многократных измерений

На практике приходится иметь дело не с генеральной совокупностью, а с конечной выборкой Х₁,Х₂,...,Х_n. Для определения оценок , d(x)пользуются соответственно:

1. среднеарифметическим выборки

2. дисперсией выборки

3. дисперсией среднего арифметического значения выборки

3. среднеквадратичным значением выборки

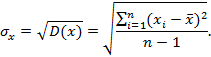
Может оказаться, что некоторые значения Х_э из выборки будут представляться слишком большими или слишком маленькими по сравнению с другими измерениями. В этом случае необходимо проверить, не являются ли эти Х_э промахами. Чтобы ответить на вопрос можно ли эти значения учитывать при расчетах , σ_X, необходимо для каждого Х_э рассчитать

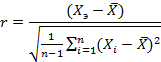
и сравнить полученные значения с табличными значениями ξ₂ (t- критерия Стьюдента). Табличное значение критерия Стьюдента определяется в зависимости от числа степеней свободы (п – 1) для выбранной доверительной вероятности α. Доверительная вероятность определяет степень достоверности прогнозируемого результата и задается до начала операции прогнозирования.

Если r>ξ₂, то Х_э необходимо исключить из дальнейшего рассмотрения. После этого необходимо пересчитать значения и D(X).

Понятно, что конечный размер выборки не позволяет считать, что X₀ = . Можно лишь утверждать, что с некоторой с заранее заданной (доверительной) вероятностью (величина |Х₀- |< , где характеризует точность оценки . Интервал ,равный , называется доверительным интервалом. При расчетах оценок погрешностей доверительная вероятность должна быть задана (выбрана) заранее.

Опыт измерений в технике показывает, что при оценке их точности вполне достаточна доверительная вероятность α, равная 0,95. Поэтому в дальнейшем будем считать, что α =0,95 (т.е. 95 % результатов измерений должны укладываться в доверительный интервал). Иногда для оценки достоверности результатов вероятностно-статистических прогнозов используют показатель, называемый уровнем значимости. Уровень значимости р показывает, какая доля выборки статистически значимо влияет на прогнозируемый результат. С другой стороны, уровень значимости указывает вероятность того, что реальный результат может не соответствовать результатам прогнозирования. Уровень значимости определяется как р=1-α.

В этом случае предельные погрешности отдельного измерения δ_хи предельная погрешность среднеарифметического значения определяются по формулам: