2.3 Уравнения Максвелла для гармонических колебаний. Комплексные амплитуды

На практике часто используются ЭМ процессы с фиксированной круговой частотой . Мгновенное значение, например, напряженности электрического поля записывается в следующем виде

(2.10)

Соответствующие значения и - это амплитуды и фазы отдельных составляющих поля (скалярные).

Запись (2.10) может быть переписана как действительная часто (Re) комплексного вектора:

(2.11)

Вектор

(2.12)

называется комплексной амплитудой поля .

Мгновенное значение вектора (2.10) в этом случае перепишется следующим образом:

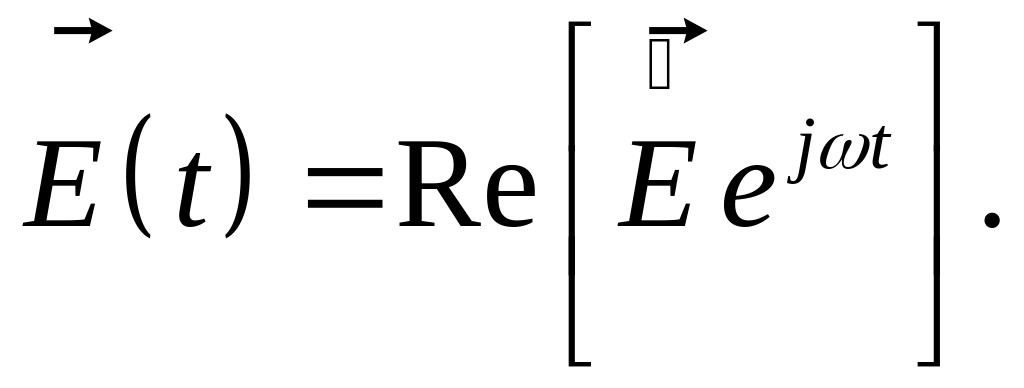(2.13)

Уравнения Максвелла могут быть теперь записаны для комплексных амплитуд. При этом надо учесть, что все векторы имеют одинаковую зависимость от времени - и что операция дифференцирования по времени заменяется умножением на величину , т.е.

С учетом этих замечаний сводка уравнений Максвелла в дифференциальной форме принимает следующий вид:

(2.14)

Такая форма системы уравнений ЭМП наиболее употребительна для практических расчетов.

Использование понятий комплексных амплитуд позволяет следующим образом переписать первое уравнение (2.14)

(2.15)

Введенная здесь величина

(2.16)

называется комплексной диэлектрической проницаемостью среды.

Число может быть изображено на комплексной плоскости (рис.2.1).

Отношение мнимой части числа к действительной называется тангенсом угла потерь

. (2.17)

В справочниках по материалам приводится эта величина для наиболее распространенных диэлектриков.

Рис. 2.1

По величине можно классифицировать материалы на хорошие или плохие диэлектрики или проводники.

2.4 Энергия электромагнитного поля

Электромагнитные поля способны накапливать, переносить и рассеивать энергию. ЭМ энергия подчиняется общему закону сохранения энергии. Из уравнений Максвелла можно вывести следующее уравнение сохранения энергии

(2.18)

Здесь - мгновенная мощность сторонних источников, находящихся внутри объема V , ограниченного поверхностью S .

Мощность тепловых потерь определяется проводимостью среды

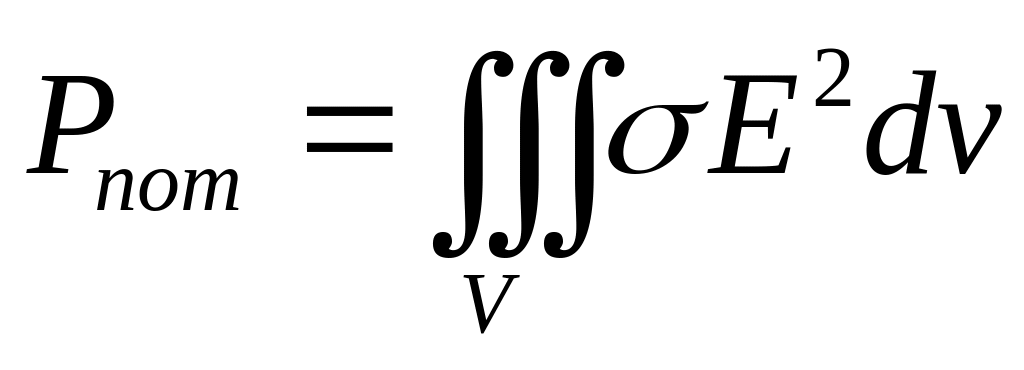
Часть энергии распределена в объеме V и называется колебательной

Наконец, еще одна часть мощности покидает объем V через поверхность S , т.е. излучается во внешнее пространство. Излучение характеризуется плотность потока мощности , которая называется вектором Пойтинга. Если векторы ЭМП меняются по гармоническому закону, то среднее за период колебаний значение вектора Пойтинга равно

(2.19)

Звездочка в (2.19) означает комплексное сопряжение.

Вектор Пойтинга имеет универсальное значение. Он характеризует не только перенос ЭМ энергии посредством излучения (антенный эффект), но и процесс направленного переноса энергии в линиях передачи (ЛП).

2.5 Граничные условия для векторов поля

Под граничными условиями в теории поля понимают правила поведения векторов поля при переходе из одной среды - в другую (на границе раздела сред). Граница раздела S и характеристики сред показаны на рис. 2.2.

Рис. 2.2.

Поскольку любой вектор может быть разделен на нормальную и тангенциальную (касательную) составляющие

то граничные условия удобно сформулировать раздельно для нормальных и тангенциальных составляющих векторов ЭМП. Эти условия сводятся к следующим положениям.

1. Нормальные составляющие векторов магнитной индукции на границе раздела сред непрерывны

(2.20)

2. Если поверхностный заряд на границе раздела сред отсутствует, то нормальные составляющие векторов электрического смещения непрерывны

(2.21)

3. Если на границе раздела равномерно распределен поверхностный заряд с удельной плотностью , то справедливо соотношение

(2.22)

4. Касательные составляющие векторов напряженности электрического поля на границе раздела сред непрерывны

5. Касательные составляющие векторов напряженности магнитного поля на границе раздела сред непрерывны

6. На поверхности хорошо проводящей среды ( ) тангенциальная составляющая магнитного поля наводит поверхностный электрический ток с плотностью . Между полем и током выполняется соотношение

(2.23)

Таким образом, магнитное поле наводит на поверхности проводника электрический ток, который перпендикулярен вектору магнитного поля .