Распределения Максвелла и Больцмана

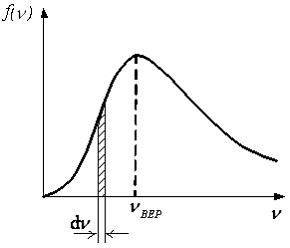
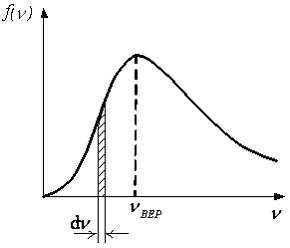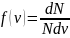№1 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где - доля молекул, скорости которых заключены в интервале скоростей от v до 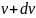в расчете на единицу этого интервала.

Для этой функции неверными являются утверждения, что …

1.При понижении температуры величина максимума функции уменьшается

2.При понижении температуры площадь под кривой уменьшается

Решение: Полная вероятность равна: 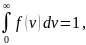то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры  не изменяется. Из формулы наиболее вероятной скорости, 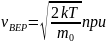и которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.

№ 2 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от  до  в расчете на единицу этого интервала. Для этой функции верными являются утверждения, что …

1.С увеличением температуры максимум кривой смещается вправо

2.При изменении температуры площадь под кривой не изменяется

№3

З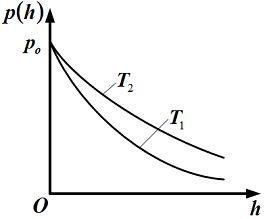 ависимости давления  идеального газа во внешнем однородном поле силы тяжести от высоты  для двух разных температур представлены на рисунке. Для графиков этих функций неверными являются утверждения, что …

1.Температура Т₁ выше температуры Т₂

2.Давление газа на высоте h равно давлению на «нулевом уровне» (h = 0), если температура газа стремиться к абсолютному нулю

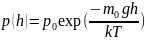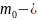Решение: Зависимость давления идеального газа от высоты  для некоторой температуры  определяется барометрической формулой: , где давление на высоте  h=0,  масса молекулы, g – ускорение свободного падения, k – постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура . Давление 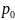 определяется весом всего газа и не меняется при изменении температуры.

№4 Н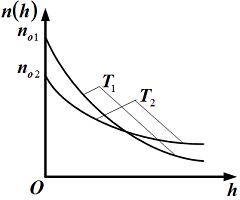 а рисунке представлены графики зависимости концентрации молекул идеального газа  от высоты  над уровнем  моря для двух разных температур –  (распределение Больцмана). Для графиков этих функций верными являются утверждения, что …

1.Температура 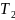выше температуры

2.Концентрация молекул газа на «нулевом уровне» (h=0) с повышением  температуры уменьшается

Решение: Зависимость концентрации молекул идеального газа от высоты для некоторой температуры Т определяется распределением Больцмана: 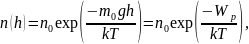где 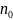концентрация молекул на высоте h=0, масса молекулы, g - ускорение свободного падения, k - постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул , и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: T₂ >T₁. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» h=0 уменьшается, а на высоте h увеличивается.

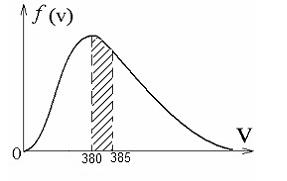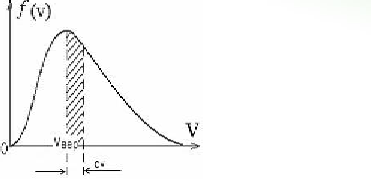
№ 5 На рисунке представлен график функции распределения молекул кислорода по скоростям(распределение Максвелла)для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей 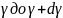в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что…

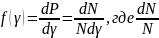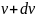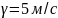Решение: Функция распределения Максвелла f( имеет смысл плотности вероятности доля молекул, скорости которых заключены в интервале от до . В нашем случае d вблизи 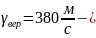наиболее вероятной скорости молекул, близкой к которой движется большее число молекул dN-число молекул, скорости которых заключены в интервале от 380 м/с до 385 м/с, N-число молекул газа. Площадь заштрихованной полоски определяет долю молекул ,скорости которых заключены в интервале от 380 м/с до 385 м/с. С ростом температуры максимум кривой смещается вправо, высота максимума убывает. Наиболее вероятная скорость 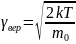зависит от температуры газа: она увеличивается с повышением температуры. Вероятность того,что величина скорости может принять хотя бы какое-нибудь значение (достоверное событие), равна единице 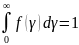поэтому при изменении температуры площадь под кривой остается равной единице. Если точно задана скорость следовательно .

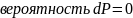№6 Формула Больцмана характеризует распределение частиц,находящихся в состоянии хаотического теплового движения ,в потенциальном силовом поле,в частности распределение молекул по высоте в изотермической атмосфере.Соотнесите рисунки и соответствующие им утверждения…

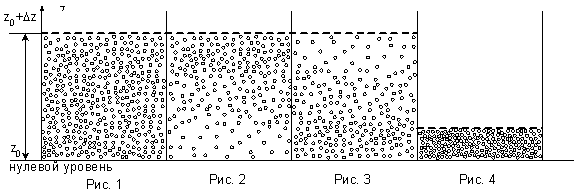
Утверждения:

Распределение молекул по кинетическим энергиям Рис.1.

Распределение молекул воздуха в атмосфере Земли Рис.3.

Распределение молекул не является больцмановским и описывается функцией Рис.2.

Распределение молекул в силовом поле при очень высокой температуре, когда энергия хаотического теплового движения значительно превосходит потенциальную энергию молекул. Рис.1.

Распределение молекул в силовом поле при температуре T . Рис.4.

Решение:

Концентрация молекул в однородном поле силы тяжести убывает с высотой по закону 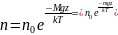(распределение Больцмана на рис.3), где n-концентрация молекул на высоте 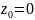, М-молярная масса, m- масса молекулы, g- ускорение свободного падения, R- универсальная газовая постоянная, k-постоянная Больцмана,T- температруа. В предельных случаях: если и молекулы равномерно распределяются по высоте (рис.1); если и молекулы располагаются на нулевом уровне (рис.4). Если число молекул,имеющих большую потенциальную энергию,увеличивается по экспоненциальному закону ,то такое распределение можно назвать «антибольцмановским», или инверсным.

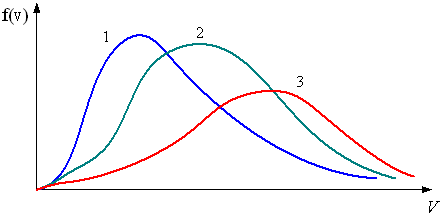№ 7 На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от  до  в расчете на единицу этого интервала. Для этих функций верными являются утверждения, что …

Решение: Функция Максвелла имеет вид 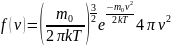Полная вероятность равна: 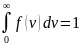, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры  не изменяется. Из формулы наиболее вероятной скорости , при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится.

Ответ: распределение 1 соответствует газу, имеющему наибольшую массу молекул (при одинаковой температуре