Средняя энергия молекул

№1 Средняя кинетическая энергия молекул газа при температуре зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место только поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекул азота равна …

№2 В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: . Здесь , где ,  и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия (He) число i равно …

№3 В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: . Здесь , где ,  и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для азота  средняя кинетическая энергия колебательного движения молекулы равна …

№4 Средняя кинетическая энергия молекулы идеального газа при температуре T равна . Здесь , При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н₂O) число i равно …

№5 Средняя кинетическая энергия молекул газа при температуре  зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, средняя кинетическая энергия молекулы кислорода ( ) равна …

№6 Если не учитывать колебательные движения в молекуле водяного пара, то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно …

№7 При комнатной температуре отношение   молярных теплоемкостей при постоянном давлении и постоянном объеме равно  для …

№8 На каждую степень свободы движения молекулы проходится одинаковая энергия, равная постоянная Больцмана, температура по шкале Кельвина). Средняя кинетическая энергия атомного водорода равна …

Распределения Максвелла и Больцмана

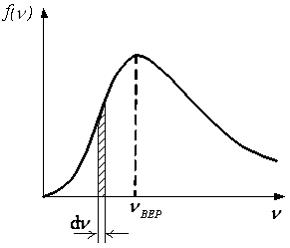№ 1 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где - доля молекул, скорости которых заключены в интервале скоростей от v до в расчете на единицу этого интервала.

Для этой функции неверными являются утверждения, что …

1.При понижении температуры величина максимума функции уменьшается

2.При понижении температуры площадь под кривой уменьшается

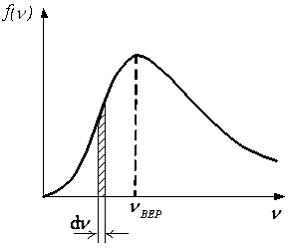№ 2 На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от  до  в расчете на единицу этого интервала. Для этой функции верными являются утверждения, что …

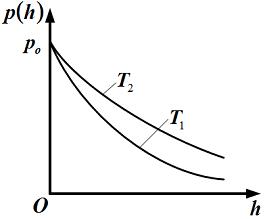№ 3 Зависимости давления  идеального газа во внешнем однородном поле силы тяжести от высоты  для двух разных температур представлены на рисунке. Для графиков этих функций неверными являются утверждения, что …

1.Температура Т₁ выше температуры Т₂

2.Давление газа на высоте h равно давлению на «нулевом уровне» (h = 0), если температура газа стремиться к абсолютному нулю

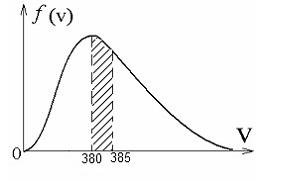
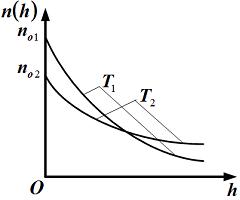№ 4 На рисунке представлены графики зависимости концентрации молекул идеального газа  от высоты  над уровнем  моря для двух разных температур –  (распределение Больцмана). Для графиков этих функций верными являются утверждения, что …

1.Температура выше температуры

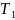
2.Концентрация молекул газа на «нулевом уровне» (h=0) с повышением  температуры уменьшается

№ 5 На рисунке представлен график функции распределения молекул кислорода по скоростям(распределение Максвелла)для температуры Т=273 К, при скорости 380 м/с функция достигает максимума. Здесь плотность вероятности или доля молекул, скорости которых заключены в интервале скоростей в расчете на единицу этого интервала. Для распределения Максвелла справедливы утверждения, что…

№6 Формула Больцмана характеризует распределение частиц,находящихся в состоянии хаотического теплового движения ,в потенциальном силовом поле,в частности распределение молекул по высоте в изотермической атмосфере.Соотнесите рисунки и соответствующие им утверждения…

Утверждения:

Распределение молекул по кинетическим энергиям Рис.1.

Распределение молекул воздуха в атмосфере Земли Рис.3.

Распределение молекул не является больцмановским и описывается функцией Рис.2.

Распределение молекул в силовом поле при очень высокой температуре, когда энергия хаотического теплового движения значительно превосходит потенциальную энергию молекул. Рис.1.

Распределение молекул в силовом поле при температуре T . Рис.4.

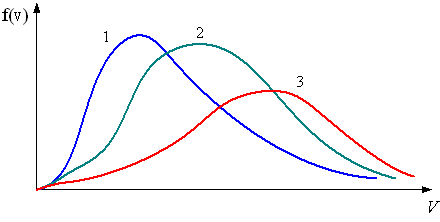№ 7 На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от  до  в расчете на единицу этого интервала. Для этих функций верными являются утверждения, что …