2.3. Проведение эксперимента

При проведении экспериментальных исследований реализуется последовательность опытов. В каждом опыте i на входы устройства подаются значения в соответствии с матрицей планирования (табл.1), измеряется выходное значение Y_i и записывается в таблицу.

Для уменьшения влияния случайных ошибок используются повторные опыты, т. е. каждая строка матрицы повторяется m раз. Выбор номера опыта следует производить случайно по времени, чтобы не было систематических ошибок. Нельзя проводить повторно подряд один и тот же опыт i.

2.4. Обработка результатов, оценка воспроизводимости эксперимента

На основе экспериментальных значений для каждой строки столбца Y рассчитывается среднее арифметическое

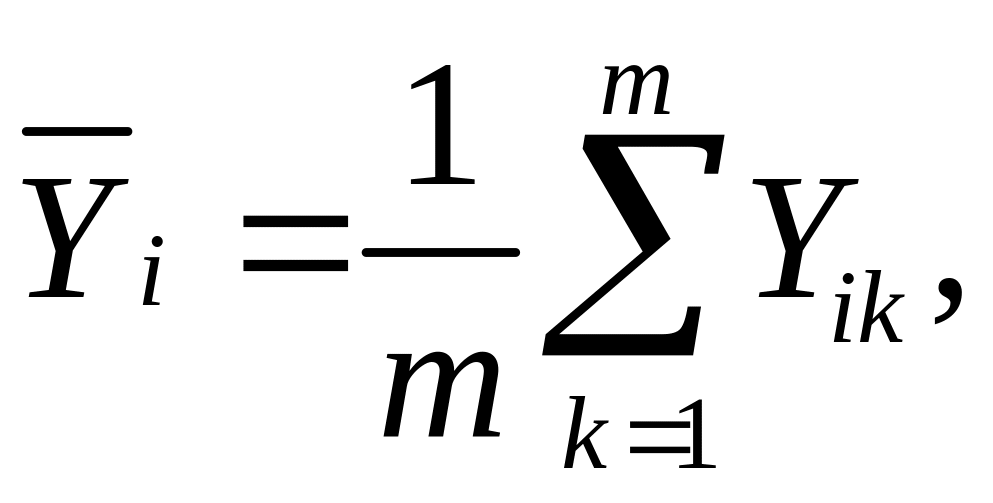
которое будет использовано для вычисления коэффициентов b, а также статистические дисперсии

.

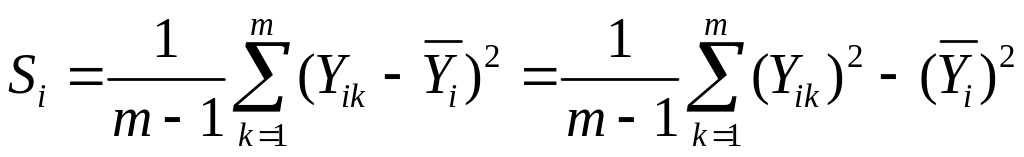Дисперсии S_i обусловлены наличием ошибок опытов (ошибок воспроизводимости). Требование однородности дисперсий является одним из требований регрессионного анализа.

Гипотеза об однородности дисперсий проверяется с помощью критерия Кохрена. При этом рассчитывается относительная величина

Гипотеза об одноразности дисперсий не отвергается, если расчетное значение G не превышает порогового G_α , т.е. G < G_α . Значение G_α находят из таблицы (прил. 1) в зависимости от уровня значимости α (чаще всего α = 5%), числа степеней свободы f₁ = m – 1 и числа опытов N. Так, например, для N = 8, f₁ = 4 имеем G_α = 0,391.

Если проверка показала, что эксперименты воспроизводимы, то их результаты можно использовать для оценки коэффициентов регрессии. В противном случае можно рекомендовать увеличить число повторных опытов.

2.5. Вычисление коэффициентов модели

Разработку модели устройства начинают с линейной. Для двух факторов она имеет вид

Y = b₀ + b₁X₁ + b₂X₂.

Коэффициенты b_j в общем случае рассчитываются по формуле

,

где выбираются из матрицы планирования. Таким образом, коэффициенты b₀, b₁, b₂ для двухфакторной модели рассчитываются следующим образом

Полный эксперимент вида N = 2ⁿ позволяет также определить независимо коэффициенты b_jk для двойных взаимодействий факторов (исключая b_jj) и более сложных. Расчет

b_jk производится по формуле

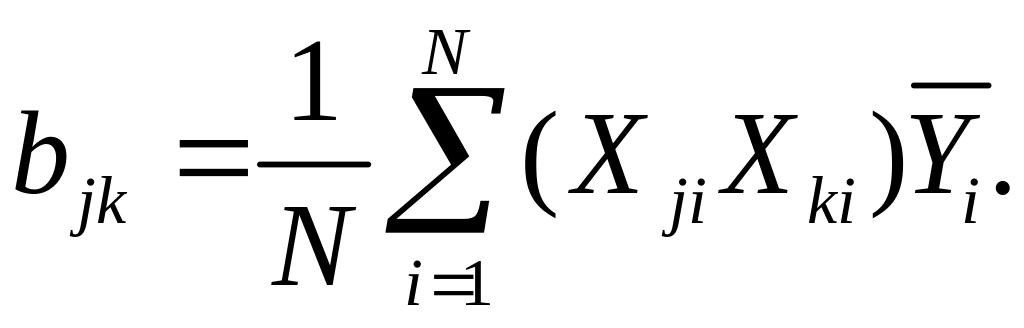
Так для двухфакторной модели в соответствии с табл. 1 коэффициент b₁₂ равен

В этом случае модель устройства будет иметь вид

В рамках эксперимента N = 2ⁿ независимо вычислить коэффициенты при квадратичных членах не возможно. Физически это объясняется недостаточным количеством уровней переменных. Для определения коэффициентов b_jj необходимо реализовать эксперимент вида N = 3ⁿ.

2.6. Проверка значимости коэффициентов модели

Проверка производится для того, чтобы упростить модель путем исключения незначимых слагаемых. Для этого значения b_j последовательно сравнивают со средним квадратическим отклонением этих коэффициентов 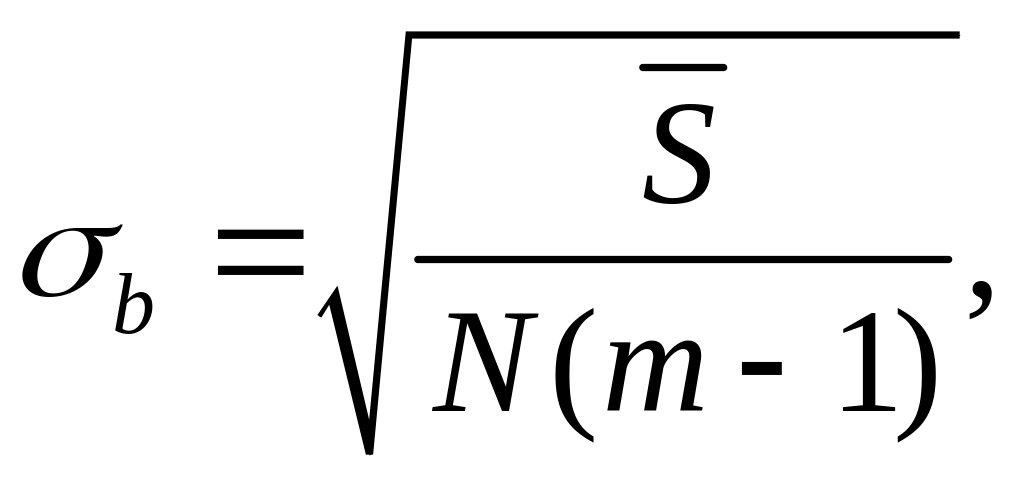где При этом отношение сравнивается с пороговым уровнем t_α выбираемым по критерию Стьюдента.

Пороговый уровень t_α берется из таблицы (прил. 2) в зависимости от уровня α (обычно берут α = 5%) и числа степени свободы f₂ = N(m – 1).

Коэффициент значим если t > t_α .