§3. Допоміжні правила виведення
1). Правило введення
кон’юнкції.
.
Формула
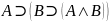- це приватний випадок тавтології, тому
цю формулу можна вивести в обчисленні
предикатів: ⊦
.
1. гіпотеза
2. гіпотеза
3. приватний випадок тавтології
4.
MP
1,2
5. MP 2,4.
2). Правило видалення кон’юнкції.
а). ⊦
1. гіпотеза
2.
приватний випадок тавтології
3. MP 1,2
б). ⊦ аналогічно.
3). Правило введення диз’юнкції.
а).
1. гіпотеза
2.
приватний випадок тавтології
3. MP 1,3
б).
аналогічно.
4). Правило видалення диз’юнкції.
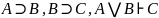
1.
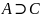гіпотеза
2. гіпотеза
3. гіпотеза
4.
приватний випадок тавтології
5.
MP 1,4
6.
MP
2,5
7. MP 3,6.
5). Правило індивідуалізації
А
.
Якщо терм
вільний для змінної
в формулі
,
то
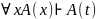
1.
гіпотеза
2.
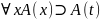(А4)
3. MP 1,2
6). Правило існування Е4.
Якщо терм
вільний для змінної
в формулі
,
то
Покажемо, що
1.
(А4)
2.
приватний випадок тавтології
3.
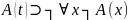MP
1,2
4. гіпотеза
5.
MP
3,4
При виведенні формул в обчисленні предикатів будемо використовувати таке твердження.
Лема1. Нехай і - формули, предметна змінна не являється вільною в формулі , тоді наступні формули являються теоремами обчислення предикатів:
1.
( і тоді за
аксіомою А4 ⊦
)
2.
(тоді за правилом Е4 ⊦
)
3.
4
.
Доведення. 1). ⊦
1. гіпотеза
2.
Gen,
1
За умовою Леми можна
застосувати теорему дедукції, тоді ⊦
.
2). ⊦
1.
гіпотеза
2.
п.1 цієї леми
3.
- приватний випадок тавтології
4.
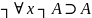MP
2,3
5. MP 1,4
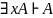за умовою Леми можна
застосувати теорему дедукції, тому ⊦
.
Так як за Е4
,
то за правилом введення & ⊦
,
що і треба було, тобто остання кон’юнкція
є
.
3). ⊦
не являється вільною
змінною формули
,
тому
- це А5. Покажем, що ⊦
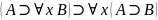
1.
гіпотеза
2. гіпотеза
3.
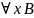MP
1,2
4. А , 3
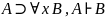
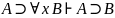теорема дедукції
Gen
В цьому виведені
застосовувалось правило Gen,
але до змінної
,
яка не являється вільною в
.
За теоремою дедукції ⊦(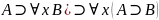
.
Залишається застосувати правило введення
&.
4). ⊦
Покажемо, що ⊦
1.
гіпотеза
2.
А
3.
приватний випадок тавтології
4.
MP
2,3
5.
Gen
4
6.
(А5)
7.
MP
5,6
8.
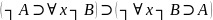- приватний випадок тавтології
9.
MP
7,8
Отримаємо
Gen застосовується тільки до , не являється вільною змінною в . Застосуємо теорему дедукції: ⊦ .
§4. Теорема про повноту
Твердження1. У всякому обчисленні предикатів першого порядку всяка теорема являється логічно загально значимою.
Доведення. Перші три
аксіомні схеми А1-А3 логічно загально
значимі. Схеми А4-А5 також ЛЗФ. Правила
виведення MP
і Gen
зберігають властивість загально
значимості, MP
– в силу того, що якщо в даній інтерпретації
істинні
,
то істинно і
(властивість 3 здійсненності формули
на послідовності), Gen
– в силу властивості 9. (
істинна в даній інтерпретації
в цій інтерпретації істинна
),
тобто всяка теорема будь-якого обчислення
предикатів логічно загально значима.
Лема Геделя. Всяка несуперечлива теорія першого порядку має злічену модель, тобто інтерпретацію, область якої – злічена множина, в якій істинні усі теореми даної теорії.
Лема про незаперечливе розширення.
Нехай К – довільна незаперечлива теорія першого порядку. Припустимо, що ┐ не виведена в теорії К. Тоді теорія К', отримана із К додаванням в якості аксіоми формули , буде також несуперечливою.
Доведення. Припустимо, що К' – суперечлива теорія, тобто існує формула така, що К' ⊦ , К'⊦┐ .
К'⊦┐
Лема із 7 пунктів. В якості
візьмемо ┐
.
К'⊦┐
.
Застосувавши 2 рази modus
ponens,
отримаємо, що К'⊦┐
.
┐
- це приватний випадок
тавтології, тому ця формула виведена в
будь-якій теорії першого порядку лише
за допомогою аксіомних схем (А1)-(А3) і
modus
ponens,
тобто правило Gen
застосовувати не треба. Далі правило
Gen
не застосовувалось, отримали, що К'⊦┐
,
значить, застосовуючи теорему дедукції
К⊦
.
– це приватний випадок
тавтології
і |
л |
л |
і |
і |
л |
і |
л |
і |
і |
л |
і |
і |
л |
За MP К⊦ , а це не так. Значить, припущення про суперечність К' не вірне.
Теорема Геделя про неповноту.
В обчисленні предикатів першого порядку теоремами являються ті і тільки ті формули, які являються логічно загально значимими.
Доведення. Враховуючи твердження1, коли залишається довести, що кожна логічно загально значима формула являється теоремою теорії К (обчислення предикатів), тобто виведена в К.
Нехай - логічно загально значима формула. Припустимо, що не виведена в теорії К. Додамо формулу ┐ до теорії К, отримаємо несуперечливу теорію К' (в Лемі про несуперечливе розширення можна поміняти і ┐ місцями).
К'=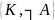
.
За Лемою Геделя існую злічена модель
(інтерпретація) для К', в якій істинні
всі аксіоми, теореми обчислення предикатів
і формула ┐
.
З іншого боку, формула логічно загально значима, значить, вона істинна і в цій інтерпретації.
Отримаємо, що існує інтерпретація, в якій істинна і ┐ істинна. Цього не може бути. Припущення не вірне.
Формула виведена в обчисленні предикатів.