
- •§1. Означення і класифікація предикатів
- •2. Класифікація предикатів
- •§2. Логічні операції над предикатами
- •§3. Квантори
- •§4. Формули логіки предикатів
- •§4. Інтерпретації
- •§5. Логічно загально значимі формули
- •§1. Теорія першого порядку к
- •§2. Теореми теорії першого порядку
- •§3. Допоміжні правила виведення
- •§4. Теорема про повноту
- •§5. Правило вибору (правило с)
§4. Інтерпретації
Інтерпретація – це система, яка
складається з: 1).
 -
не порожня множина(область інтерпретації);
2). Деяка відповідність, що відноситься
до кожної предикатної букви
- деякий n-місний предикат
-
не порожня множина(область інтерпретації);
2). Деяка відповідність, що відноситься
до кожної предикатної букви
- деякий n-місний предикат
 , кожній функціональній букві
деяку n-місну операцію
, кожній функціональній букві
деяку n-місну операцію

 ,
кожній предметній постійній
,
кожній предметній постійній
 - деякий елемент з області
.
- деякий елемент з області
.
Формули логіки предикатів мають сенс тільки тоді, коли вказана яка-небудь інтерпретація символів, які входять в ці формули.
В даній інтерпретації всяка формула без вільних змінних представляє собою висловлювання, яке істинне або хибне, а всяка формула з вільними змінними – деякий предикат на області інтерпретації, істинний, можливо, для одних значень і хибний – для інших.
Приклад1.
 -
область інтерпретації
-
область інтерпретації
Предикат


В даній інтерпретації розглянемо формули:
а).
 б).
б).

Формула а) – це двомісний предикат
 ,
істинний для всіх упорядкованих пар
,
істинний для всіх упорядкованих пар
 чисел
чисел
 ,
для яких
,
для яких
 .
.
Формула б) – це одномісний предикат:
“для кожного натурального числа
 ”.
Для будь-якого значення
”.
Для будь-якого значення
 цей предикат має значення (тотожно-хибне).
цей предикат має значення (тотожно-хибне).
в).
 - одномісний предикат:
- одномісний предикат:
 .
Цей предикат являється тотожно-істинним.
.
Цей предикат являється тотожно-істинним.
г).
 .
Нехай в нашій інтерпретації предметній
константі
.
Нехай в нашій інтерпретації предметній
константі
 ставиться
у відповідність такий елемент з області
ставиться
у відповідність такий елемент з області
 .
Для даної інтерпретації формула 2) –
висловлювання:
.
Для даної інтерпретації формула 2) –
висловлювання:

 .
Тотожно-істинне.
.
Тотожно-істинне.
Нехай дана деяка інтерпретація з областю
 Ɛ-
множина усіх парних послідовних елементів
з
.
Ɛ-
множина усіх парних послідовних елементів
з
.

Візьмемо деяку послідовність
 .
Нехай
.
Нехай
 ,
що відображає множину всіх термів в
області
за такими правилами:
,
що відображає множину всіх термів в
області
за такими правилами:
Якщо терм
-
це предметна змінна
,
то
 ,
де
,
де
 -
це елемент послідовності
-
це елемент послідовності
 .
.
Якщо терм
-
це предметна постійна
 ,
то
,
то
 ,
де
,
де
 - це інтерпретація константи
.
- це інтерпретація константи
.
Якщо терм
 ,
де
-
це функціональна буква, а
- терми, то
,
де
-
це функціональна буква, а
- терми, то
 .
(
-
це операція, яка інтерпретує функціональну
букву
).
.
(
-
це операція, яка інтерпретує функціональну
букву
).
Приклад2. Нехай
 ,
,
 ,
,
 .
Нехай
.
Нехай
 ,
терм
,
терм
 Знайдемо
Знайдемо
 .
.
 ,
,

Для вичислення треба зробити наступне:
1). В термі
замінити

2). Виконати операції
.
В нашому прикладі2

Дамо означення здійснимості формули
на послідовності
 .
.
1). Якщо
- елементарна формула
 ,
- відповідний предикат в інтерпретації,
то формула
виконана на послідовності
тоді і тільки тоді, коли
,
- відповідний предикат в інтерпретації,
то формула
виконана на послідовності
тоді і тільки тоді, коли

2). Формула
 виконана на
тоді і тільки тоді, коли формула
не виконана на
.
виконана на
тоді і тільки тоді, коли формула
не виконана на
.
3). Формула
виконана на
тоді і тільки тоді, коли формула
не виконана на
або коли формула
 виконана на
.
виконана на
.
4). Формула
 виконана на
тоді і тільки тоді, коли формула
виконана на будь-якій послідовності
виконана на
тоді і тільки тоді, коли формула
виконана на будь-якій послідовності
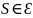 ,
яка відрізняється від
не більш ніж своєю
,
яка відрізняється від
не більш ніж своєю
 -тою
компонентою.
-тою
компонентою.
Означення. Формула називається істинною(в даній інтерпретації) тоді і тільки тоді, коли вона виконана на всякій послідовності із Ɛ.
Означення. Формула називається хибною(в даній інтерпретації) тоді і тільки тоді, коли вона не виконана ні на одній послідовності із Ɛ.
Властивості поняття здійснимості формули на послідовності.
хибна в даній інтерпретації
 істинна, і
істинна
хибна.
істинна, і
істинна
хибна.
Доведення. Нехай формула
являється хибною в даній інтерпретації.
Тоді
 формула
не виконана на
формула
не виконана на
 виконана на
,
виконана на
,
 істинна в даній інтерпретації. Справедливе
і обернене твердження.
істинна в даній інтерпретації. Справедливе
і обернене твердження.
істинна
 - хибна доводиться аналогічно.
- хибна доводиться аналогічно.
Ніяка формула не може бути одночасно істинною та хибною в одній інтерпретації. (Це випливає з означення).
Якщо в даній інтерпретації формули
 істинні, то істинна і формула
.
істинні, то істинна і формула
.
Доведення.
- істинні в даній інтерпретації.
Припустимо, що
не являється істинною. Тоді
 на
формула
не виконана. Формули
виконані на
на
формула
не виконана. Формули
виконані на
 формула
виконана на
.
Отримали протиріччя.
формула
виконана на
.
Отримали протиріччя.
Формула
являється хибною в даній інтерпретації
 - істинна,
- хибна.
- істинна,
- хибна.
Доведення. Нехай формула
- хибна. Тоді
формула
не виконана на
 виконана на
і
не виконана на
,
виконана на
і
не виконана на
,
 - істинна,
- хибна. Справедливе і обернене твердження.
- істинна,
- хибна. Справедливе і обернене твердження.
Формула
 виконана на послідовності
виконана на послідовності
 виконана на
і
виконана на
.
виконана на
і
виконана на
.
Доведення:
 .
.
 виконана на
виконана на
 не виконана на
не виконана на

Формула
 виконана на послідовності
виконана на
або
виконана на
.
виконана на послідовності
виконана на
або
виконана на
.
Доведення.
=
.
 виконана на
виконана на
 не виконана на
або
виконана на
виконана на
або
виконана на
.
не виконана на
або
виконана на
виконана на
або
виконана на
.
Формула
виконана на послідовності
 виконана на
і
виконана на
,
або
не виконана на
і
не виконана на
.
виконана на
і
виконана на
,
або
не виконана на
і
не виконана на
.
Доведення.
=
.
 виконана на
виконана на

Формула
 виконана на
виконана на
 формула
виконана хоча б на одній послідовності
формула
виконана хоча б на одній послідовності
 ,
яка відрізняється від
не більш, ніж одною
-тою
компонентою.
,
яка відрізняється від
не більш, ніж одною
-тою
компонентою.
Доведення.
- це

 виконана на
виконана на
 не виконана на деякій послідовності
не виконана на деякій послідовності
 ,
яка відрізняється від
не більш, ніж своєю
-тою
компонентою
виконана
на
,
від
не більш, ніж
-тою
компонентою.
,
яка відрізняється від
не більш, ніж своєю
-тою
компонентою
виконана
на
,
від
не більш, ніж
-тою
компонентою.
Формула
істинна в даній інтерпретації
в цій інтерпретації істинна формула
 .
.
Доведення.
істинна
виконана
 виконана
.
виконана
.
Означення. Замиканням даної формули назвемо формулу, яка виходить приписуванням до зліва знаків кванторів загальності, що містять у порядку спадання індексів усі вільні змінні, що входять в .
Приклад. Нехай
є
 .
Тоді замиканням
буде
.
Тоді замиканням
буде
 .
.
Якщо формула не містить вільних змінних, то змиканням будемо називати саму формулу .
Нехай вільні змінні(якщо вони є) формули
містяться серед змінних
 .
Тоді якщо у послідовностей
і
компоненти з номерами
.
Тоді якщо у послідовностей
і
компоненти з номерами
 співпадають, то формула
виконана на
співпадають, то формула
виконана на
 на
.
на
.
Для доведення цього твердження знадобиться:
Лема. Якщо змінні терма
зустрічаються серед
,
а у послідовностей
і
компоненти з номерами
співпадають, то
 .
.
Доведення. 1.
 ,
,

Отримаємо, що .
Ясно, що це справедливо для
 .
.
2.
 (предметна константа)
(предметна константа)
 (за означенням формули
(за означенням формули
 і
і
 )
)
3. Припустимо, що твердження леми вірне
для термів
 ,
усі змінні яких містяться серед
,
тобто
,
усі змінні яких містяться серед
,
тобто
 .
.
Розглянемо терм
 .
.
 .
Лема доведена.
.
Лема доведена.
Доведемо твердження 10. Доведення проведемо індукцією за числом кванторів і зв'язок у формулі .
Нехай
- це елементарна формула
 .
Так як змінні цієї формули будуть
змінними термів
,
значить вони всі містяться серед
.
За лемою
.
.
Так як змінні цієї формули будуть
змінними термів
,
значить вони всі містяться серед
.
За лемою
.
Нехай формула
виконана на послідовності
,
тоді
 виконана на
.
Справедливо і обернене.
виконана на
.
Справедливо і обернене.
Індуктивне припущення: твердження вірне
для всіх формул з числом зв'язок і
кванторів меншим від К. Розглянемо
формулу
,
у якої рівно К зв'язок і кванторів.
Можливі три варіанти:
 ,
,
 ,
,

а). Нехай
- це
 (
має К-1 зв'язку, квантор). Нехай
виконана на
(
має К-1 зв'язку, квантор). Нехай
виконана на
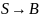 не виконана на
(за
індуктивним припущенням)
не виконана на
не виконана на
(за
індуктивним припущенням)
не виконана на
 виконана на
.
В обернений бік аналогічно.
виконана на
.
В обернений бік аналогічно.
б). Нехай
- це
 (кожна формула
і
(кожна формула
і
 мають число зв'язок і кванторів
мають число зв'язок і кванторів
 ).
).
Нехай
виконана на
 виконана на
або
не виконана на
виконана на
або
не виконана на
 виконана на
.
В обернений бік аналогічно.
виконана на
.
В обернений бік аналогічно.
в). Нехай
– це
 ..
..
1. - не являється вільною змінною формули .
Нехай
виконана на
виконана на
і на всіх послідовностях
 ,
які відрізняються від
не більш ніж
,
які відрізняються від
не більш ніж
 -тою
компонентою.
не
міститься серед
,
тому за індуктивним припущенням формула
виконана на
і на всіх послідовностях
,
які відрізняються від
не більш ніж
-тою
компонентою
-тою
компонентою.
не
міститься серед
,
тому за індуктивним припущенням формула
виконана на
і на всіх послідовностях
,
які відрізняються від
не більш ніж
-тою
компонентою виконана на
.
Аналогічно і обернене.
виконана на
.
Аналогічно і обернене.
2. - вільна змінна формули .
Тоді
міститься серед
.
Нехай
виконана на
виконана на
і на всіх послідовностях
,
які відрізняються від
не більш ніж
-тою
компонентою (за індуктивним припущення)
виконана на
і на всіх послідовностях
(за індуктивним припущення)
виконана на
і на всіх послідовностях
 виконана на
.
Аналогічно і обернене.
виконана на
.
Аналогічно і обернене.
Означення. Формулу називають замкнутою, якщо вона співпадає зі своїм замиканням.
Наприклад, всяка формула без вільних змінних являється замкнутою.
11. Якщо формула замкнута, то в кожній інтерпретації вона або істинна, або хибна.
(Зауваження: при цьому формула може бути істинна в одних інтерпретаціях і хибна в інших).
Доведення.
- замкнута, тобто не має вільних змінних.
Застосуємо властивість 10. Множина
змінних
з попереднього пункту, зараз порожня.
Виходить, що, якщо
виконана на деякій послідовності
,
то
виконана на виконана на будь-якій
послідовності
 являється
істинною в даній інтерпретації. Якщо
не виконана на деякій послідовності
,
то
не виконана
являється
істинною в даній інтерпретації. Якщо
не виконана на деякій послідовності
,
то
не виконана
 являється хибною в даній інтерпретації.
являється хибною в даній інтерпретації.
Зауваження. Незамкнута, тобто, яка
містить вільні змінні, формула
може в деяких інтерпретаціях бути і не
істинною, і не хибною. Так, наприклад,
формула
і інтерпретації
 виконана лише на послідовностях
виконана лише на послідовностях
 таких, що
таких, що
 .
Тобто, в цій інтерпретації формула
не істинна і не хибна.
.
Тобто, в цій інтерпретації формула
не істинна і не хибна.
