§2. Логічні операції над предикатами

Означення1. Запереченням n-місного предиката , визначеного на множинах , називається новий n-місного предикат, визначений на тих самих множинах, що позначається (невірно, що Р), який перетворюється в істинне висловлювання при всіх тих і тільки тих значеннях предметних змінних, при яких початкове висловлювання перетворюється в хибне.

Означення 2. Кон'юнкцією n-місного предиката , визначеного на множинах , і m-місного предиката , визначеного на множинах , називається новий - місний предикат, визначений на множинах , що позначається , який перетворюється в істинне висловлювання при всіх тих і тільки тих значеннях предметних змінних, при яких обидва початкові предикати перетворюються в істинне висловлювання.

Означення 3. Диз'юнкцією n-місного предиката , визначеного на множинах , і m-місного предиката , визначеного на множинах , називається новий - місний предикат, визначений на множинах , що позначається , який перетворюється в істинне висловлювання, якщо хоча б один з початкових предикатів істинний.

Означення 4. Слідуванням n-місного предиката , визначеного на множинах , і m-місного предиката , визначеного на множинах , називається новий - місний предикат, визначений на множинах , що позначається , який стає хибним тільки в тому випадку, коли перший предикат істинний, а другий – хибний.

Означення 5. Еквіваленцією n-місного предиката , визначеного на множинах , і m-місного предиката , визначеного на множинах , називається новий - місний предикат, визначений на множинах , що позначається , який перетворюється в істинну тоді і тільки тоді, коли обидва початкові предикати істинні, або обидва хибні.

§3. Квантори

Операцією зв'язування квантором спільності називається правило, за яким кожному одномісному предикату , визначеному на множині , зіставляється висловлювання (для будь-якого х істинне висловлювання), яке істинне в тому і тільки тому випадку, коли предикат тотожно істинний і хибне в противному випадку.

Операцією зв'язування квантором спільності за змінною 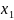називається правило, за яким кожному n-місному предикату , визначеному на множинах , ставиться у відповідність новий (n-1)-місний предикат

§4. Формули логіки предикатів

Алфавіт логіки предикатів наступний:

1). - предметні змінні

2). - предметні константи

3). - функціональні букви. Вони використовуються для позначення операцій. Індекс означає розмірність функції, тобто кількість змінних, індекс -її назва.

4). - предикатні букви. Використовуються для позначення предикатів. Індекс означає розмірність, використовується, щоб розрізняти предикатні букви однієї розмірності.

5). (,) – дужки, коми.

6). - логічні зв'язки.

7). - квантор спільності.

Довільну скінчену послідовність символів алфавіта будемо називати виразом. В множині усіх виразів виокремимо дві підмножини: термів та формул.

Означення.

1). Будь-яка предметна змінна, будь-яка предметна константа являється термом;

2). Якщо - функціональна буква, а - терми, то являється термом;

3). Термами являються ті і тільки ті вирази, для яких це випливає з 1) та 2).

Наприклад, 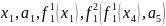- терми, - не терми.

Означення. Якщо - предикатна буква, а - терми, то - елементарна формула. Наприклад, .

Дамо означення формули логіки предикатів.

Означення.

1). Будь-яка елементарна формула являється формулою логіки предикатів;

2). Якщо - формули логіки предикатів, - предметна змінна, то вирази являються формулами;

3). Формулами являються ті і тільки ті вирази, для яких це випливає з перших двох пунктів.

Будемо використовувати знаки , для скороченого запису формул:

- це

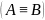- це

- це

Вираз будемо розглядати, як скорочений запис формули .

Правила зняття дужок залишаються такими самими, як і в логіці висловлювань. Логічні зв'язки були упорядковані таким чином: , . Домовимося додатково вважати, що квантори розташовані за силою між зв'язками ⋁ та ⊃: ,

У виразі формула називається областю дії квантора .

Входження змінної х в деяку формулу будемо називати зв'язним, якщо х являється змінною квантора , що входить в цю формулу, або знаходиться в області дії квантора .

Якщо входження змінної не є зв'язним, то називаємо його вільним.

Наприклад,

св. св. св. связ. связ. св.

Змінну називаємо вільною в даній формулі, якщо існує вільне входження цієї змінної в цю формулу. Змінну називаємо зв'язною в даній формулі, якщо існує зв'язне входження цієї змінної в цю формулу. Змінна може бути одночасно і вільною, і зв'язною в одній формулі.

Приклад:

- зв'язна і вільна

- вільна

- вільна

Означення. Терм називається вільним змінної , якщо ніяке вільне входження змінної в формулу не лежить в області дії ніякого квантора , де - змінна, що входить в терм .

Терм не вільний для змінної якщо існує вільне входження змінної яке знаходиться в області дії квантора, взятого по одній із змінних даного терма.

Приклад: формула:

Терм: Вільний для змінної

Не являється вільним для в формулі .

Властивості:

Будь-який терм, що не містить змінних, вільний для будь-якої змінної в будь-якій формулі. Приклад: .

Терм вільний для будь-якої змінної в формулі , якщо ніяка змінна терма не являється зв'язаною змінною в .

Терм вільний для якщо не містить вільних входжень або взагалі не містить у своєму записі.

вільний для в будь-якій формулі.