
- •§1. Означення і класифікація предикатів
- •2. Класифікація предикатів
- •§2. Логічні операції над предикатами
- •§3. Квантори
- •§4. Формули логіки предикатів
- •§4. Інтерпретації
- •§5. Логічно загально значимі формули
- •§1. Теорія першого порядку к
- •§2. Теореми теорії першого порядку
- •§3. Допоміжні правила виведення
- •§4. Теорема про повноту
- •§5. Правило вибору (правило с)
Логіка предикатів
§1. Означення і класифікація предикатів
В граматиці предикат (присудок) – слово (або декілька слів) в реченні, яке виражає, що говорить про суб'єкт (підмет).
«Має чорний колір», «заздрить», «є дійсне число», «Джон любить дівчат, не старших 20 років».
«Будь-яке раціональне число є дійсне число» і «3 – раціональне число», то «3 є дійсне число».
В обчисленні висловлювань не можна встановити логічність цього міркування. Додавши три додаткових логічних поняття (терм, предикат и квантор) можна символізувати дуже багато в звичайній і математичній мові так, що стає можливо аналізувати міркування.
Вираз « »
не є висловлюванням. Підставляючи
замість
»
не є висловлюванням. Підставляючи
замість
 числа 7, 15, отримаємо хибне висловлювання,
а, підставляючи 0, 1, 2, отримаємо істинне
висловлювання. Кожному числу із
числа 7, 15, отримаємо хибне висловлювання,
а, підставляючи 0, 1, 2, отримаємо істинне
висловлювання. Кожному числу із
 відповідає значення цього виразу істинно
або хибно, тобто воно є функцією
(одномісною), визначеною на множини
(зі значеннями {0,1}.
відповідає значення цього виразу істинно
або хибно, тобто воно є функцією
(одномісною), визначеною на множини
(зі значеннями {0,1}.
Наприклад, « »,
»,
 :
при х=2, у=10 вираз істинний; при
х=0, у=-10 вираз хибний. Воно визначає
двомісну функцію, визначену на множині
:
при х=2, у=10 вираз істинний; при
х=0, у=-10 вираз хибний. Воно визначає
двомісну функцію, визначену на множині
 зі значеннями {0,1}.
зі значеннями {0,1}.
«х та у – батьки z» - трьохмісна функція, визначена на множині *, М і людей зі значеннями із множини {0,1}.
Означення. Визначеним на множинах
 n-місним предикатом
називається речення, яке містить n
предметних змінних
n-місним предикатом
називається речення, яке містить n
предметних змінних
 ,
яке перетворюється у висловлювання при
підстановці замість цих змінних
,
яке перетворюється у висловлювання при
підстановці замість цих змінних
 конкретних елементів (предмети) із
множин
відповідно.
конкретних елементів (предмети) із
множин
відповідно.




Наприклад:
 ,
тобто визначені на
,
тобто визначені на
 .
.
 - це двомісний предикат, визначений на
.
- це двомісний предикат, визначений на
.


2. Класифікація предикатів
Предикат
 ,
заданий на множинах
називається:
,
заданий на множинах
називається:
Тотожно істинний, якщо при
підстановці замість предметних змінних
 будь-яких конкретних предметів
будь-яких конкретних предметів
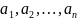 із
множин
відповідно він перетворюється в істинне
висловлювання
із
множин
відповідно він перетворюється в істинне
висловлювання
 .
Наприклад,
.
Наприклад,

Тотожно хибний, якщо при
підстановці замість предметних змінних
будь-яких конкретних предметів
із
множин
відповідно він перетворюється в хибне
висловлювання
.
Наприклад,

Здійсненим (спростовний), якщо
 щонайменше один набір конкретних
предметів
щонайменше один набір конкретних
предметів
 із
множин
із
множин
 відповідно, при підстановці яких замість
відповідних предметних змінних в
предикат
відповідно, при підстановці яких замість
відповідних предметних змінних в
предикат
 останній перетвориться в істинне(хибне)
висловлювання
останній перетвориться в істинне(хибне)
висловлювання
 .
.
 –
здійснений, він же спростовний.
–
здійснений, він же спростовний.
Кожний тотожно істинний предикат є здійсненим(обернено ні).
Кожний тотожно хибний предикат є спростовним(обернено ні).
Кожний не тотожно істинний предикат буде спростовним, але, взагалі кажучи, не буде тотожно хибним.
Кожний не тотожно хибний предикат буде здійсненим, але, взагалі кажучи, не буде тотожно істинним.
Означення. Множиною істинності предиката
,
заданого на множинах
 називається сукупність усіх упорядкованих
n-систем
називається сукупність усіх упорядкованих
n-систем
 ,
в яких
,
в яких
 таких, що даний предикат перетворюється
в істинне висловлювання
таких, що даний предикат перетворюється
в істинне висловлювання
 при підстановці
при підстановці
 Наприклад,
Наприклад,

Множина істинності
 множині
пар дійсних чисел, які являються
координатами точок площини, що утворюють
окружність з центром на початку координат
і радіусом 3.
множині
пар дійсних чисел, які являються
координатами точок площини, що утворюють
окружність з центром на початку координат
і радіусом 3.
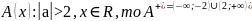
а). Тотожно істинний предикат

б). Тотожно хибний предикат

в). Здійснений

г). Спростовний

Означення. Два предикати
і
 ,
задані на однакових множинах
називаються рівносильними, якщо набір
предметів
,
задані на однакових множинах
називаються рівносильними, якщо набір
предметів
 перетворює перший предикат в істинне
висловлювання
тоді і тільки тоді, коли цей набір
предметів перетворює другий предикат
в істинне висловлювання
перетворює перший предикат в істинне
висловлювання
тоді і тільки тоді, коли цей набір
предметів перетворює другий предикат
в істинне висловлювання
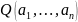 .
Позначається
.
Позначається

У шкільній математиці рівняння і нерівності – це предикати. Розв'язком є пошук їхніх множин істинності. Важливі рівносильні перетворення.

 - рівносильні на множині
- рівносильні на множині
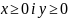 і не рівносильні на множині
і не рівносильні на множині

Означення. Предикат
,
заданий над множинами
називається наслідком предиката
,
заданого над тими самими множинами,
якщо він перетворюється в істинне
висловлювання на всіх тих наборах
значень предметних змінних із відповідних
множин, на яких в істинне висловлювання
перетворюється предикат



 являється наслідком
являється наслідком
 ,
заданих на N.
,
заданих на N.
