8 Прикладные задачи

1 Метод Гаусса—Зайделя

Последовательное продвижение осуществляется путем поочередного варьирования каждым фактором до достижения частного экстремума целевой функции.

В каждой серии опытов изменяется только переменная x_i, остальные остаются неизменными. Изображающая точка перемещается попеременно вдоль каждой из координатной осей x_i (i= ) факторного пространства.

Переход к новой (i+1)-й координате осуществляется при достижении частного экстремума целевой функции F(x) по предыдущей координате, т.е. в точке x_N+1, где (рис. 14.1, а)

.

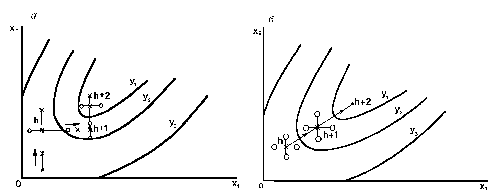
Рис. 14.1. Движение в факторном пространстве в методах

Гаусса-Зайделя (а) и градиента (б)

Направление движения вдоль (i+1)-й координатной оси выбирается обычно по результатам двух пробных экспериментов в окрестностях точки частного экстремума по предыдущей переменной. Поиск экстремума прекращается в точке, движение из которой в любом направлении не приводит к увеличению значения выходного параметра.

Н.: При увеличении количества независимых переменных до 5—6 применение метода Гаусса‑Зайделя для оптимизации ТП становится малоэффективным в силу увеличения числа экспериментов.

Метод градиента

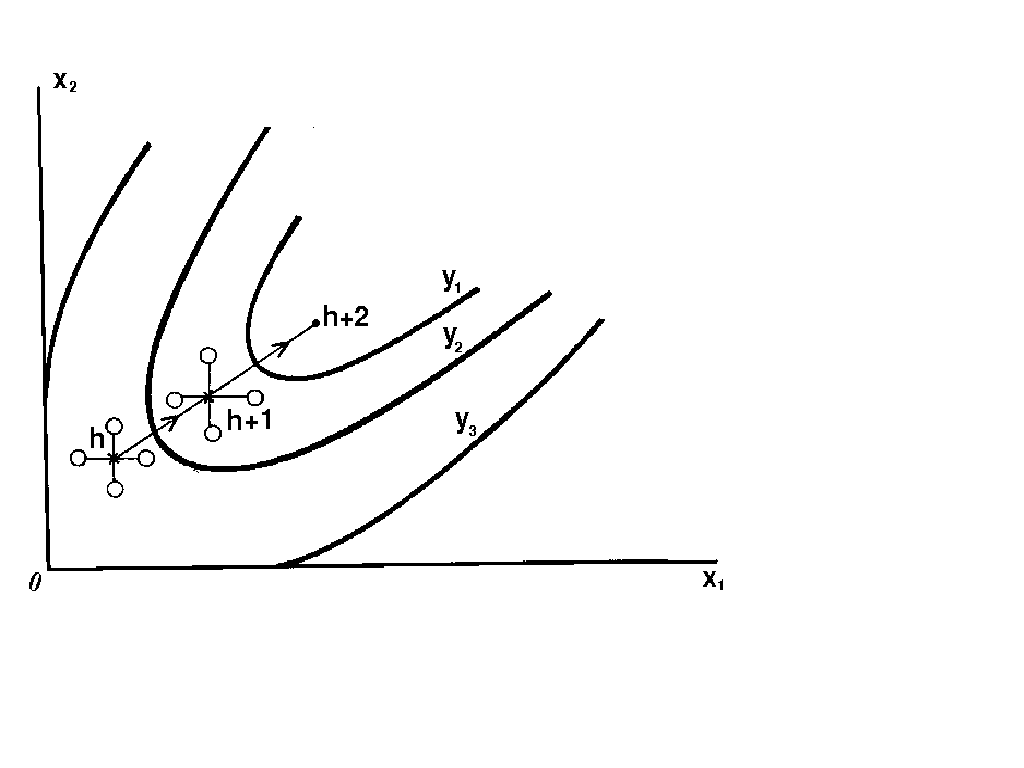
б

Рис. 14.1 Движение в факторном пространстве в методах

Гаусса-Зайделя (а) и градиента (б)

При оптимизации градиентным методом движение совершается в направлении наибольшего изменения целевой функции, причем направление движения корректируется после каждого рабочего шага. Поскольку координатами вектора

служат коэффициенты при линейных членах уравнения регрессии b₁, b₂,...,b_k, то их можно определить по результатам нескольких пробных экспериментов в окрестностях исходной точки. В этом случае приращение целевой функции F соответствующее приращению x_i, можно считать пропорциональным значению частной производной:

.

После нахождения составляющих градиента выполняется рабочий шаг по направлению к экстремуму (рис. 14.1, б):

,

где _ш — параметр рабочего шага, который выбирают в зависимости от его номера h или расстояния от оптимума :

,

где  — const; h — номер шага; .

Показателем выхода в область оптимума является малое значение модуля градиента

,

т. е. все коэффициенты b_i становятся незначимыми или равными нулю.

Н.: В градиентном методе важен выбор шага. При слишком малом шаге требуется большое количество экспериментов, а если размер шага велик, то можно "проскочить" оптимум.

Метод крутого восхождения (Бокса—Уилсона)

Этот метод объединяет характерные элементы методов Гаусса‑Зайделя и градиента. Так, шаговое движение при этом методе осуществляется в направлении наибольшего изменения функции (в направлении градиента), но в отличие от метода градиента корректировка направления движения производится не после каждого шага, а после достижения частного экстремума целевой функции, как при методе Гаусса—Зайделя.

Практически поиск оптимума методом крутого восхождения выполняется следующим образом:

1) вблизи исходной точки x₀ проводится эксперимент для определения grad F(x₀), результаты эксперимента подвергаются статистическому анализу, определяются коэффициенты b_i уравнения;

2) вычисляется произведение b_ix_i , где x_i — шаг варьирования параметра x_i при исследовании поверхности отклика в окрестностях исходной точки. Фактор, для которого произведение будет максимальным, принимается за базовый _бx_б;

3) для базового фактора выбирается шаг движения _б по направлению к оптимуму, после этого вычисляются размеры шагов при крутом восхождении по остальным переменным процесса; при движении к оптимуму по градиенту все исследуемые параметры должны изменяться пропорционально коэффициентам наклона поверхности отклика b_i:

;

4) проводятся "мысленные" опыты, которые заключаются в вычислении по уравнению

значений целевой функции в точках факторного пространства, лежащих на пути к экстремуму; при этом i-я координата n-й точки

,

где h= ; i= ; .

Прогнозируемое значение выходного параметра

;

5)поскольку каждый цикл крутого восхождения приближает к поверхности отклика с большой крутизной, рекомендуется для каждой последующей серии опытов выбирать шаг меньший, чем в предыдущей;

6)эксперимент прекращается, когда все или почти все коэффициенты b_i уравнения получаются незначимыми или равными нулю, что говорит о выходе в область экстремума целевой функции.

15