Правила округлення:

1. Якщо перша з відкинутих цифр менше 5, то десяткові знаки, які залишилися, зберігаються без змін.

2. Якщо перша з відкинутих цифр більше 5 або дорівнює 5 і серед інших відкинутих цифр є ненульові, то до останньої цифри, що залишилася, додається одиниця.

3. Якщо перша з відкинутих цифр дорівнює 5 і інші відкинуті цифри є нульовими, то остання цифри, що залишилася, не змінюється, якщо вона парна, і збільшується на одиницю, якщо вона непарна.

Приклад 3. Округлити число до семи, шести, п’яти і т.д. десяткових знаків і до одиниць.

Розв’язання. За правилом округлення:

(за правилом 3);

(за правилом 2);

(за правилом 2);

(за правилом 1);

(за правилом 2);

(за правилом 2);

(за правилом 1);

(за правилом 2).

Абсолютна і відносна похибки записуються у вигляді чисел з одною або двома значущими цифрами, і вони округлюються з надлишком. В записі наближених чисел вони вказуються так:

;

Так, для числа з прикладу 1б)

; .

Приклад 4. Виділити вірні значущі цифри наступних чисел:

1) ; ;

2) ; ;

3) ; .

Розв’язання. Виділимо вірні значущі цифри підкреслюванням.

1) , оскільки ;

2) , оскільки ;

3) , оскільки .

Похибки округлення в ЕОМ числа , які обумовлені скінченністю розрядної сітки, для різних комп’ютерів можуть бути обчислені за формулою:

,

де – перша значуща (відмінна від нуля) цифра; – основа системи числення, що використовується в комп’ютері; – розрядність комп’ютера ( для стандартної точності і для подвійної точності – для ЕОМ типу IBM).

6. Дії над наближеними числами. Похибки обчислень

Нехай , і задані абсолютні і відносні похибки їх наближень, тобто: , ; , .

Сформулюємо правила обчислення похибок при виконуванні операцій над наближеними числами.

1. При додаванні або відніманні двох наближених чисел їх абсолютні похибки додаються:

.

2. При множенні або діленні двох наближених чисел їх відносні похибки додаються:

;

.

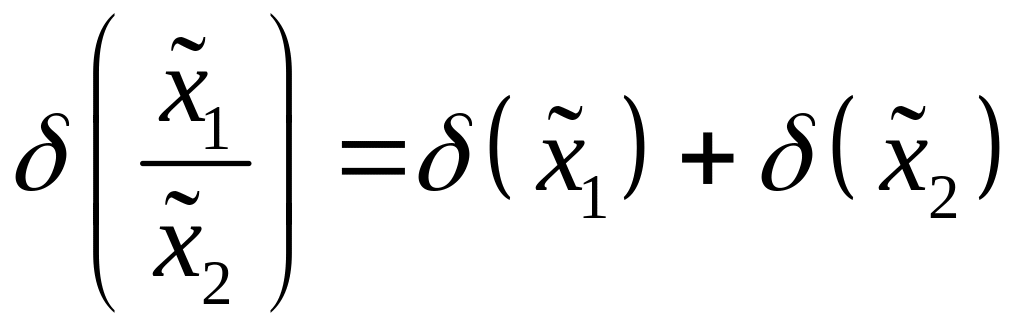3. При піднесенні до степеня наближеного числа його відносна похибка множиться на показник степеня:

4. Відносна похибка суми додатних доданків міститься між найбільшим і найменшим значеннями відносних похибок цих доданків:

,

де , .

На практиці для оцінки похибки приймають найбільше значення .

Приклад.

Поряд з наведеними вище правила обчислення похибок деяких дій над наближеними числами можна записати аналогічні правила і для обчислення значень функцій, аргументами яких є наближені числа. Найбільш повним є загальне правило, засноване на обчисленні приросту (похибки) функції при заданих приростах (похибках) аргументів.

Розглянемо функцію однієї змінної . Нехай – наближене значення аргументу , – його абсолютна похибка. абсолютну похибку функції можна вважати її приростом, який вона набуває при зміні аргументу на . З курсу математичного аналізу відомо (), що цей приріст можна замінити диференціалом:

.

Тоді для абсолютної похибки функції отримаємо вираз:

.

Аналогічний вираз можна записати для функції декількох змінних. Так, для абсолютної похибки функції , наближені значення аргументів якої відповідно, абсолютна похибка має вигляд:

,

де , , – абсолютні похибки аргументів.

Відносна похибка знаходиться за формулою:

.

Отримані співвідношення можна використовувати для виведення похибок довільної функції. Зокрема, таким способом легко отримати вирази правил 1-3 обчислення похибок.