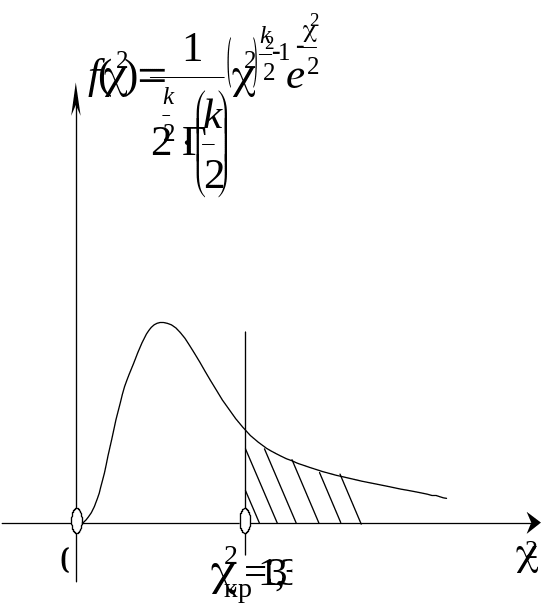
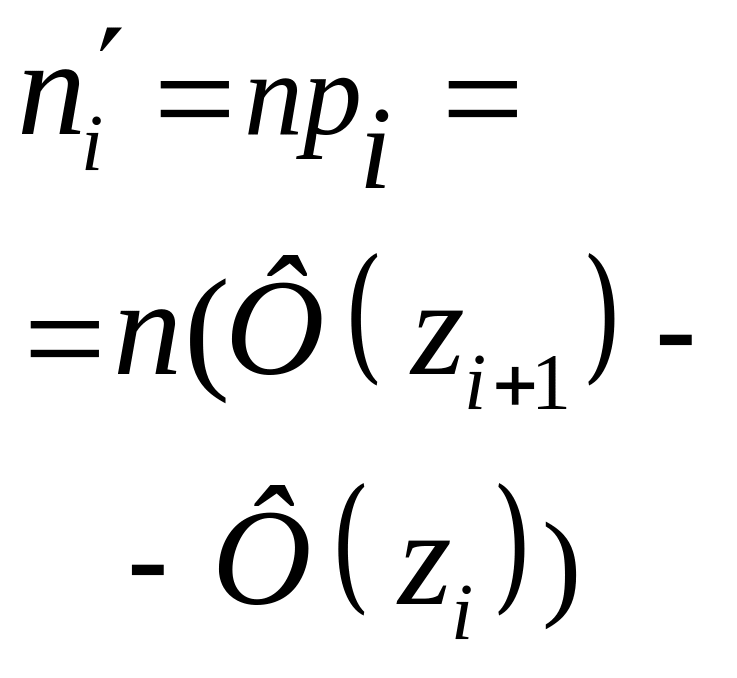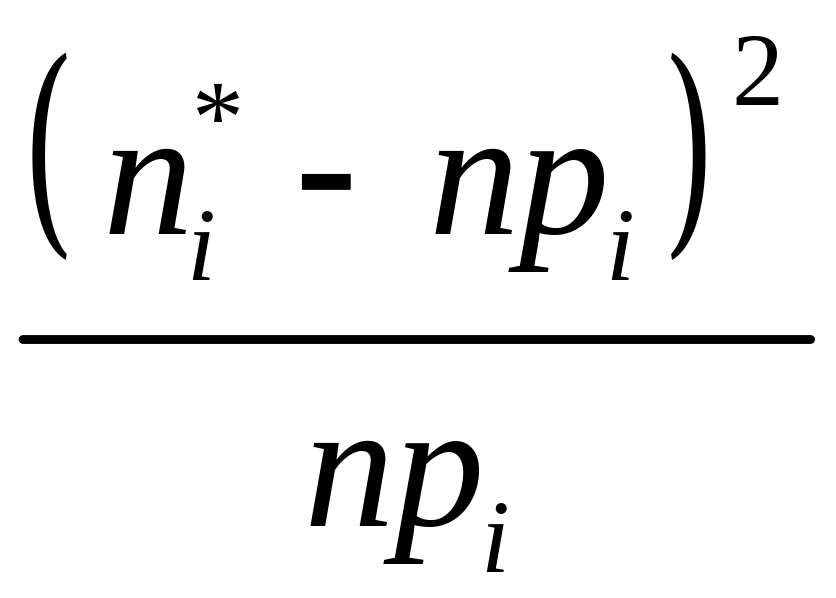- •Лекція № 11 Тема: Перевірка статистичних гіпотез
- •1. Поняття статистичної гіпотези.
- •1. Поняття статистичної гіпотези
- •2. Критична область. Основний принцип статистичної перевірки статистичних гіпотез
- •3. Загальний алгоритм перевірки правильності нульової гіпотези
- •4. Перевірка гіпотез про математичне сподівання
- •5. Критерій узгодження Пірсона
5. Критерій узгодження Пірсона
Нехай
досліджується генеральна сукупність
випадкової величини
і необхідно перевірити нульову статистичну
гіпотезу
:
випадкова величина
підлягає закону розподілу
![]() .
Для перевірки нульової гіпотези здійснимо
вибірку з
незалежних випадкових спостережень
.
Для перевірки нульової гіпотези здійснимо
вибірку з
незалежних випадкових спостережень
![]() над
випадковою величиною
.
Як відомо, за результатами вибірки можна
побудувати емпіричну функцію розподілу
над
випадковою величиною
.
Як відомо, за результатами вибірки можна
побудувати емпіричну функцію розподілу
![]() .
Порівняння емпіричного і теоретичного
законів розподілу проводиться за
допомогою критеріїв узгодження.
Найчастіше використовують критерій
узгодження Пірсона (критерій
).
Розглянемо цей критерій.
.
Порівняння емпіричного і теоретичного
законів розподілу проводиться за
допомогою критеріїв узгодження.
Найчастіше використовують критерій
узгодження Пірсона (критерій
).
Розглянемо цей критерій.
Розіб’ємо
всю область значень випадкової величини
на
![]() інтервалів і підрахуємо кількість
елементів
інтервалів і підрахуємо кількість
елементів
![]() ,
які потрапили в кожний з інтервалів
,
які потрапили в кожний з інтервалів
![]() .
Оскільки теоретична функція розподілу
відома, то, використовуючи
формулу
.
Оскільки теоретична функція розподілу
відома, то, використовуючи
формулу
![]() ,
можемо
обчислити ймовірності
,
можемо
обчислити ймовірності
![]() попадання значень величини
в інтервал
та теоретичні частоти
попадання значень величини
в інтервал
та теоретичні частоти
![]() ,
,
![]() .
.
За
критерій перевірки нульової гіпотези
беруть критерій узгодження Пірсона –
випадкову величину, що має розподіл
![]() ,
спостережуване значення якої визначається
за формулою
,
спостережуване значення якої визначається
за формулою
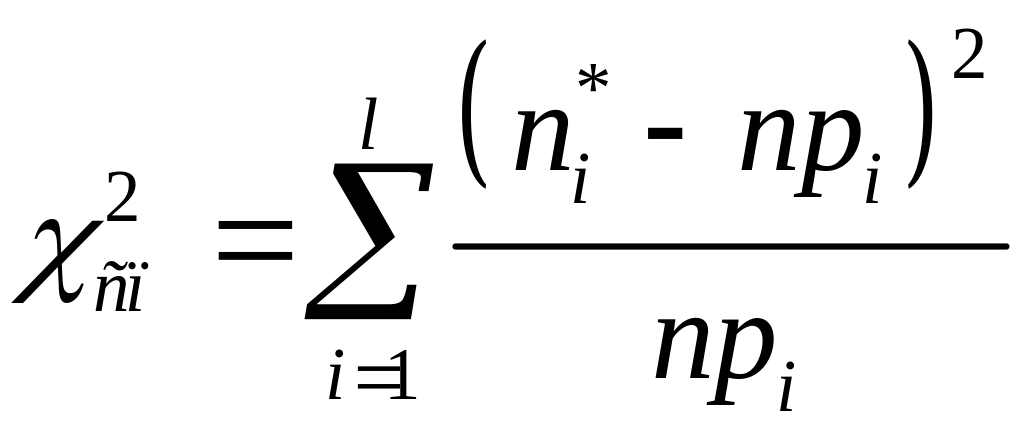 , (2)
, (2)
і має
![]() ступенів вільності,
ступенів вільності,
де — число часткових інтервалів інтервального статистичного розподілу вибірки;
![]() — число
параметрів, якими визначається закон
розподілу ймовірностей генеральної
сукупності згідно з нульовою гіпотезою.
Так, наприклад, для закону Пуассона,
який характеризується одним параметром
,
— число
параметрів, якими визначається закон
розподілу ймовірностей генеральної
сукупності згідно з нульовою гіпотезою.
Так, наприклад, для закону Пуассона,
який характеризується одним параметром
,
![]() ,
для нормального закону
,
для нормального закону
![]() ,
оскільки
цей закон визначається двома параметрами
,
оскільки
цей закон визначається двома параметрами
![]() i
i
![]() .
.
Зауваження. У статистиці кількістю степенів вільності певної величини часто називають різницю між кількістю випробувань і кількістю величин, знайдених завдяки цим випробуванням незалежно одної від другої.
Очевидно,
чим менше відрізняються вибіркові і
теоретичні частоти, тим менше
![]() .
Доведено, що при
.
Доведено, що при
![]() розподіл (2) прямує до розподілу
з k
степенями вільності незалежно від
розподілу генеральної сукупності.
розподіл (2) прямує до розподілу
з k
степенями вільності незалежно від
розподілу генеральної сукупності.
Побудуємо правосторонню критичну область, виходячи з вимоги, щоб ймовірність попадання критерію в цю область в припущенні вірності нульової гіпотези дорівнювала рівню значущості :
![]() .
.
Отже,
правостороння критична область
визначається нерівністю
![]() ,
а область прийняття нульової гіпотези
– нерівністю
,
а область прийняття нульової гіпотези
– нерівністю
![]() .
За результатами вибірки обчислюємо
спостережуване значення критерію
.
За результатами вибірки обчислюємо
спостережуване значення критерію
![]() і за таблицею критичних точок розподілу
і за таблицею критичних точок розподілу
![]() при заданому рівні значущості
і числу ступенів вільності
знаходимо критичну точку.
при заданому рівні значущості
і числу ступенів вільності
знаходимо критичну точку.
![]() .
Якщо
.
Якщо
![]() ,
то нульова гіпотеза
приймається, в протилежному випадку
,
то нульова гіпотеза
приймається, в протилежному випадку
![]() – нульова гіпотеза відхиляється.
– нульова гіпотеза відхиляється.
Зауваження. Формулу (2) можна переписати у вигляді
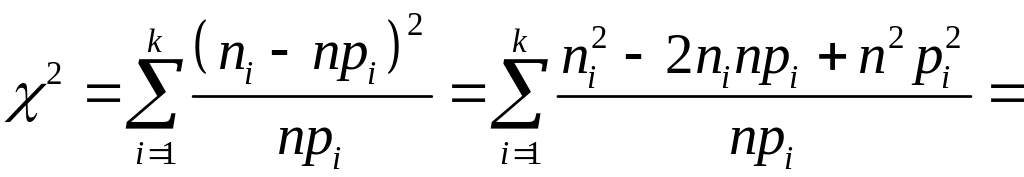
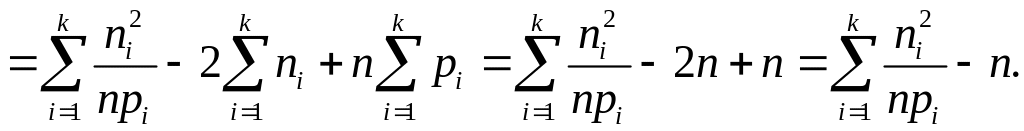
Співвідношення
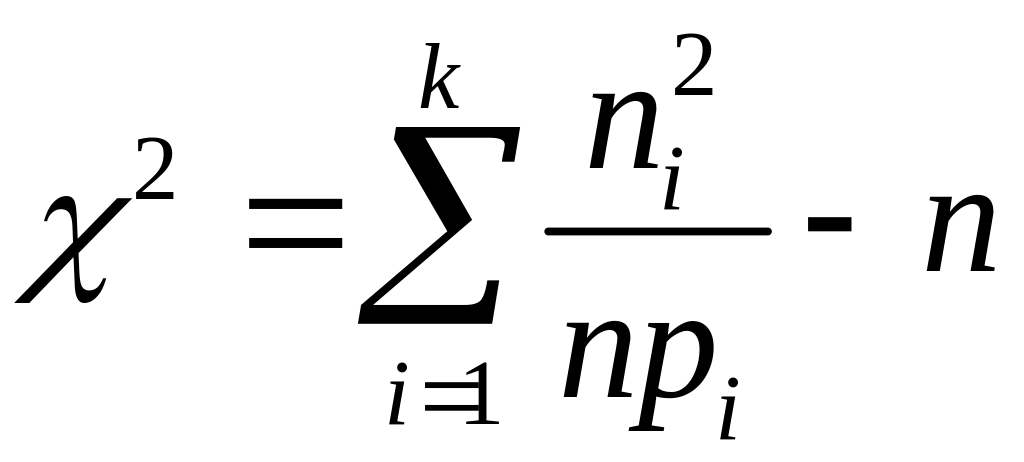 (3)
(3)
використовується для контролю правильності обчислень.
Приклад. За заданим інтервальним статистичним розподілом випадкової величини — маси новонароджених дітей —
-
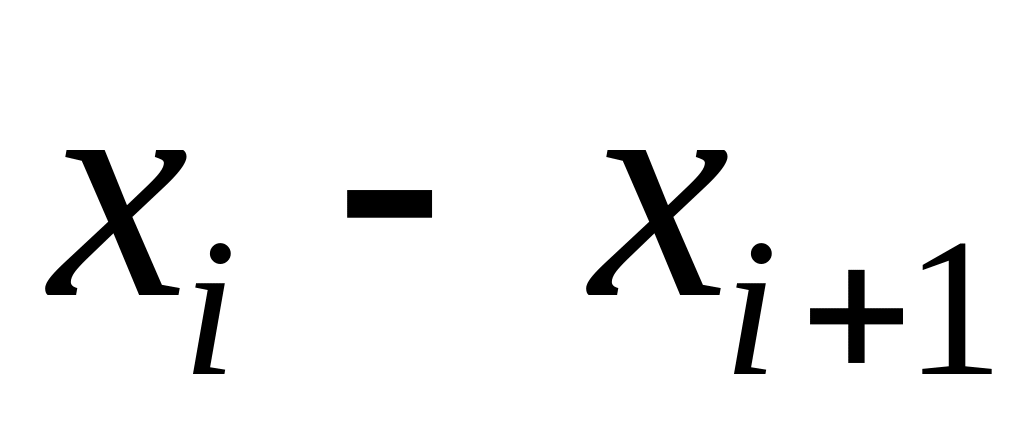
1—1,5
1,5—2
2—2,5
2,5—3
3—3,5
3,5—4
4—4,5
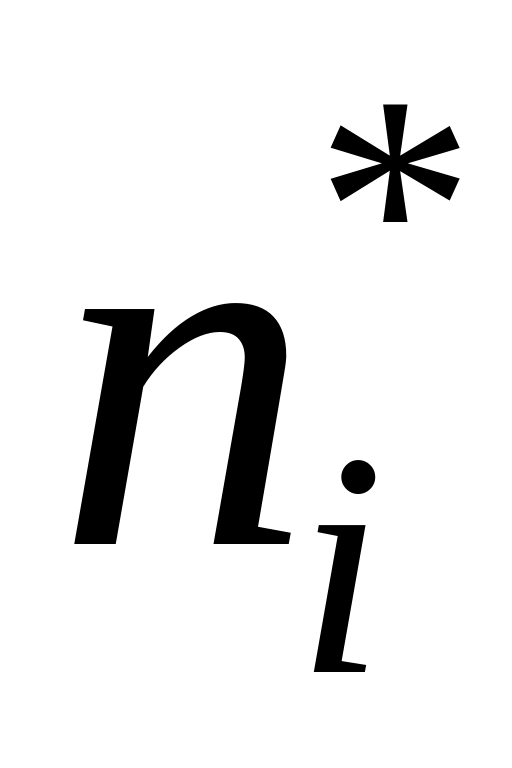
10
20
50
35
28
15
12
при
рівні значущості
перевірити правильність гіпотези
![]() про нормальний закон розподілу ознаки
Х
— маси новонароджених дітей.
про нормальний закон розподілу ознаки
Х
— маси новонароджених дітей.
Розв’язання.
Для визначення теоретичних частот
![]() необхідно обчислити
,
необхідно обчислити
,
![]() .
.
Побудуємо відповідний дискретний статистичний розподіл:
-
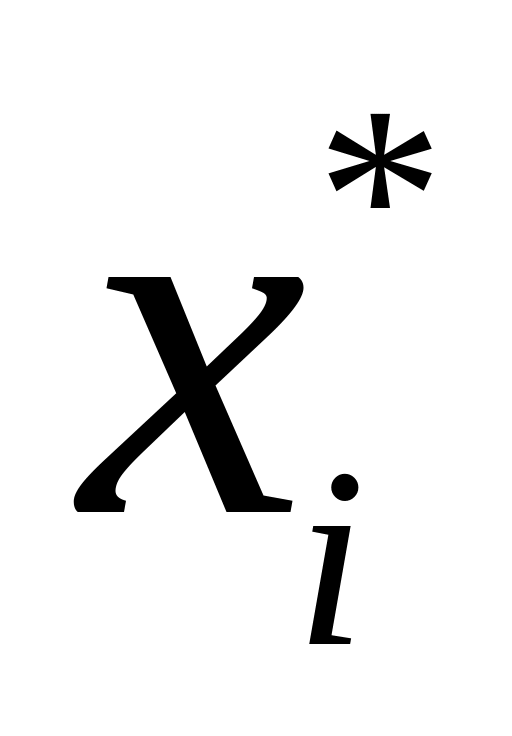
1,25
1,75
2,25
2,75
3,25
3,75
4,25
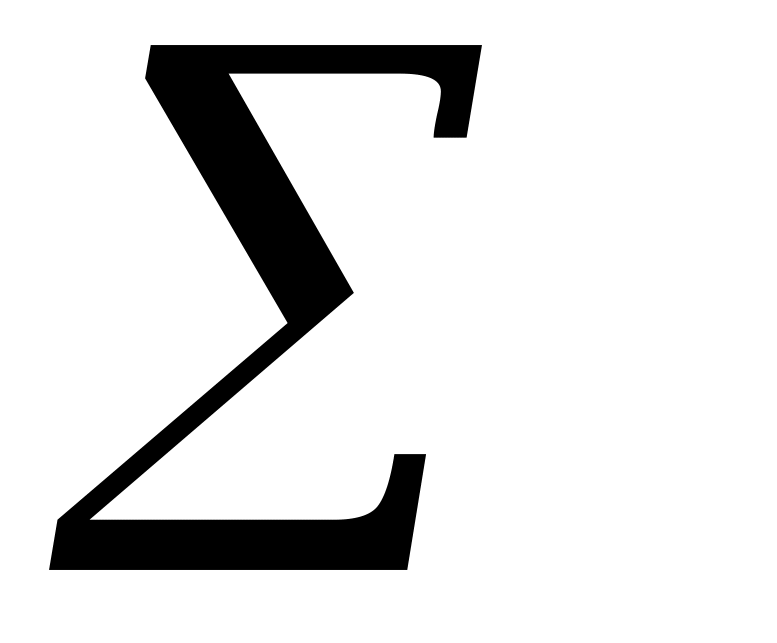
10
20
50
35
28
15
12
170
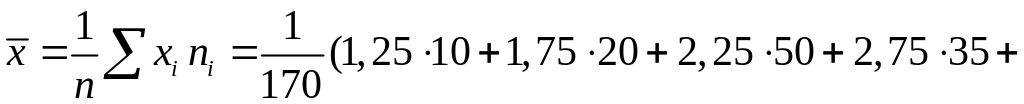
![]()
![]() ;
;
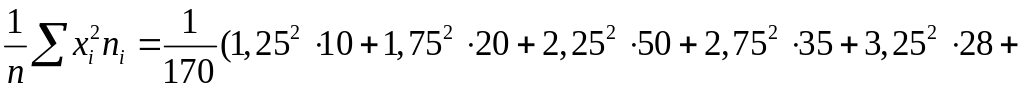
![]()
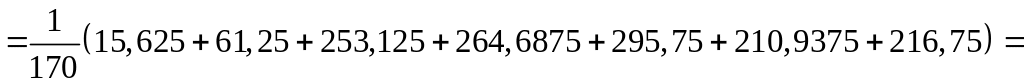
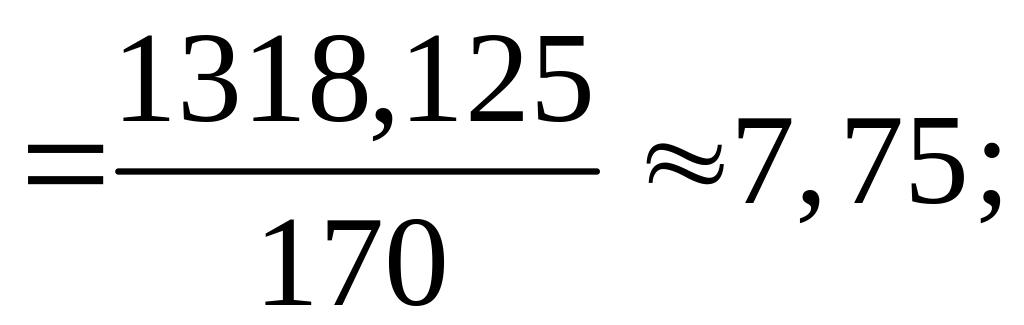
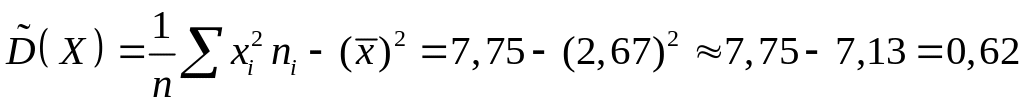 ;
;
![]() .
.
Обчислення теоретичних частот подано в таблиці:
xi |
xi+1 |
|
|
|
|
|
|
1 |
1,5 |
10 |
–2,11 |
–1,48 |
–0,4830 |
–0,4306 |
9 |
1,5 |
2 |
20 |
–1,48 |
–0,85 |
–0,4306 |
–0,3023 |
23 |
2 |
2,5 |
50 |
–0,85 |
–0,22 |
–0,3023 |
–0,0871 |
38 |
2,5 |
3 |
35 |
–0,22 |
0,42 |
–0,0871 |
0,1628 |
44 |
3 |
3,5 |
28 |
0,42 |
1,05 |
0,1628 |
0,3531 |
33 |
3,5 |
4 |
15 |
1,05 |
1,68 |
0,3531 |
0,4535 |
17 |
4 |
4,5 |
12 |
1,68 |
2,32 |
0,4535 |
0,4898 |
6 |
Обчислимо
спостережуване значення критерію
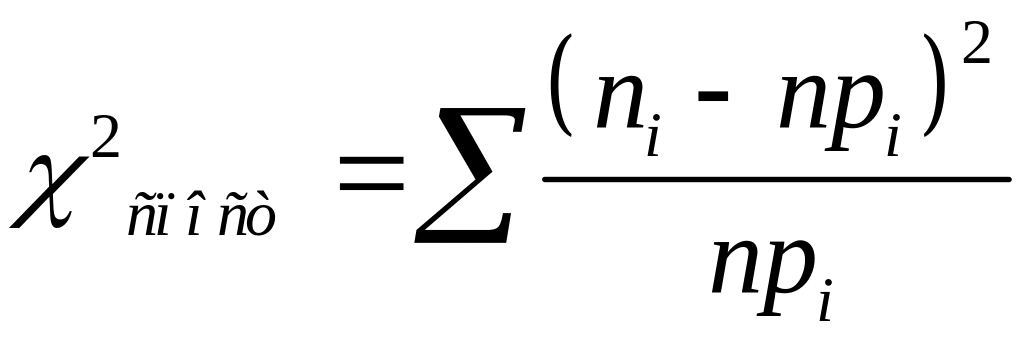 ,
для чого складемо розрахункову таблицю
,
для чого складемо розрахункову таблицю
|
|
|
|
|
|
|
|||
10 |
9 |
1 |
1 |
0,11 |
100 |
11,11 |
|||
20 |
23 |
–3 |
9 |
0,39 |
400 |
17,39 |
|||
50 |
38 |
12 |
144 |
3,79 |
2500 |
65,79 |
|||
35 |
44 |
–9 |
81 |
1,84 |
1225 |
27,84 |
|||
28 |
33 |
–5 |
25 |
0,76 |
784 |
23,76 |
|||
15 |
17 |
–2 |
4 |
0,23 |
225 |
13,23 |
|||
12 |
6 |
6 |
36 |
6 |
144 |
24,00 |
|||
|
170 |
170 |
|
|
13,12 |
|
183,12 |
||
Отже, маємо
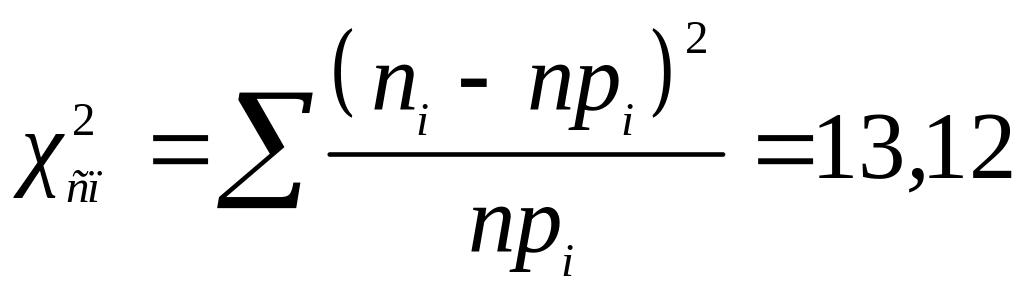 .
.
Для контролю правильності обчислень використаємо співвідношення
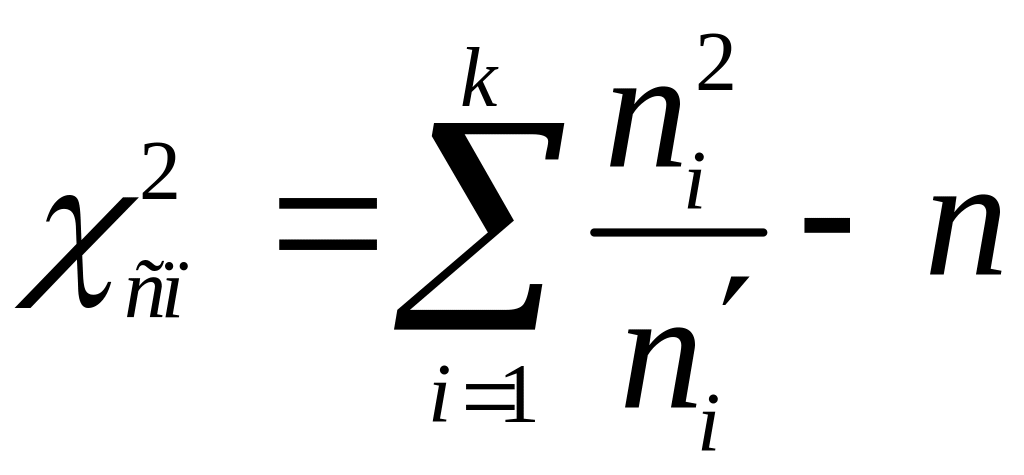 :
183,12–170=13,12.
:
183,12–170=13,12.
Отже, обчислення виконані правильно.
Знайдемо
число степенів вільності
![]() ,
враховуючи,
що число груп вибірки
,
враховуючи,
що число груп вибірки
![]() ,
а число параметрів нормального розподілу
,
а число параметрів нормального розподілу
![]() :
:
![]() .
.
В таблиці
критичних точок розподілу
![]() ,
за рівнем значущості
,
за рівнем значущості
![]() та числом степенів вільності
та числом степенів вільності
![]() знаходимо
знаходимо
![]() .
.
Статистичне
рішення:
Оскільки 13,12 =
![]() =13,3,
то відмінність емпіричних та теоретичних
частот незначуща. Значить, дані
спостережень узгоджуються з гіпотезою
про нормальний розподіл генеральної
сукупності.
=13,3,
то відмінність емпіричних та теоретичних
частот незначуща. Значить, дані
спостережень узгоджуються з гіпотезою
про нормальний розподіл генеральної
сукупності.
Таким чином, гіпотеза про нормальний закон розподілу генеральної сукупності ознаки приймається.
Правостороння критична область показана на малюнку: