4. Перевірка гіпотез про математичне сподівання

Нехай генеральна сукупність випадкової величини розподілена за нормальним законом , причому параметр – математичне сподівання – нам невідоме, але є підстави вважати, що воно дорівнює . Задача полягає в тому, щоб при заданому рівні значущості  перевірити нульову гіпотезу . Оскільки математичне сподівання оцінюється за результатами вибірки через вибіркове середнє значення , то задачу можна переформулювати так: встановити, значимо, чи ні відрізняється вибіркове середнє значення від математичного сподівання . Для гіпотези можливі три альтернативні гіпотези: , і .

Припустимо, що дисперсія генеральної сукупності відома. За критерій перевірки нульової гіпотези візьмемо випадкову величину

,

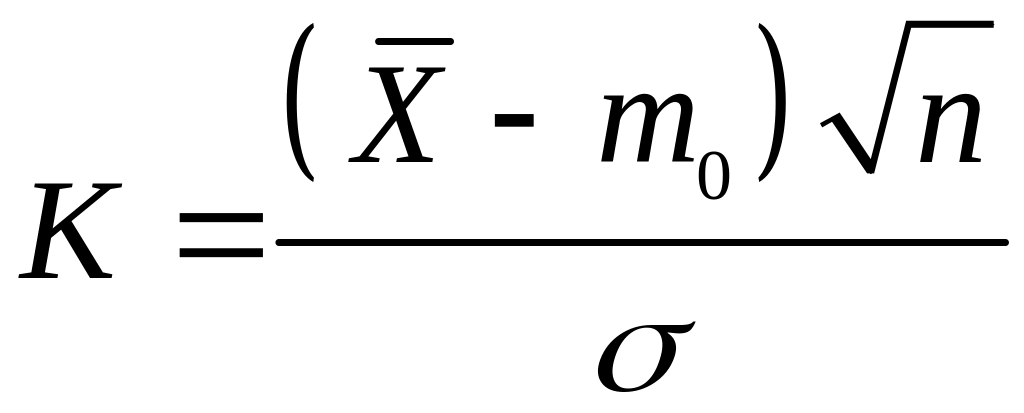Ця величина розподілена за нормованим нормальним законом .

1. Для того, щоб при заданому рівні значущості перевірити нульову гіпотезу при альтернативній гіпотезі потрібно обчислити спостережуване значення критерію

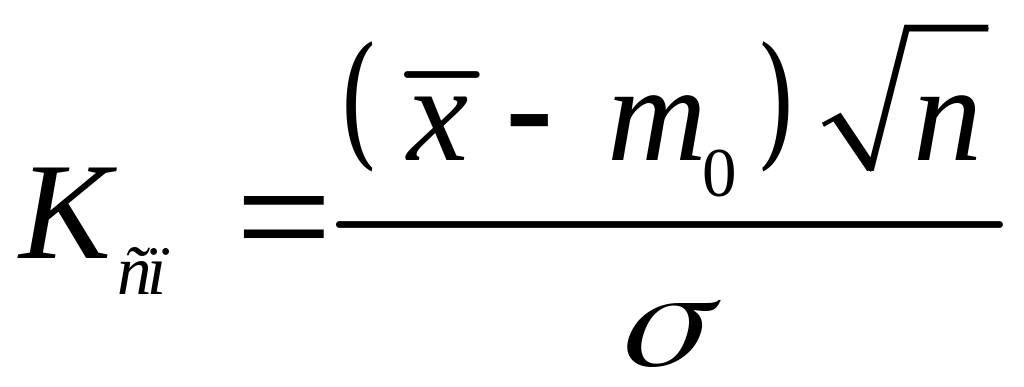(1)

і за таблицею значень функції Лапласа знайти критичну точку правосторонньої критичної області з рівняння . Якщо , то нульову гіпотезу приймають, якщо – відхиляють.

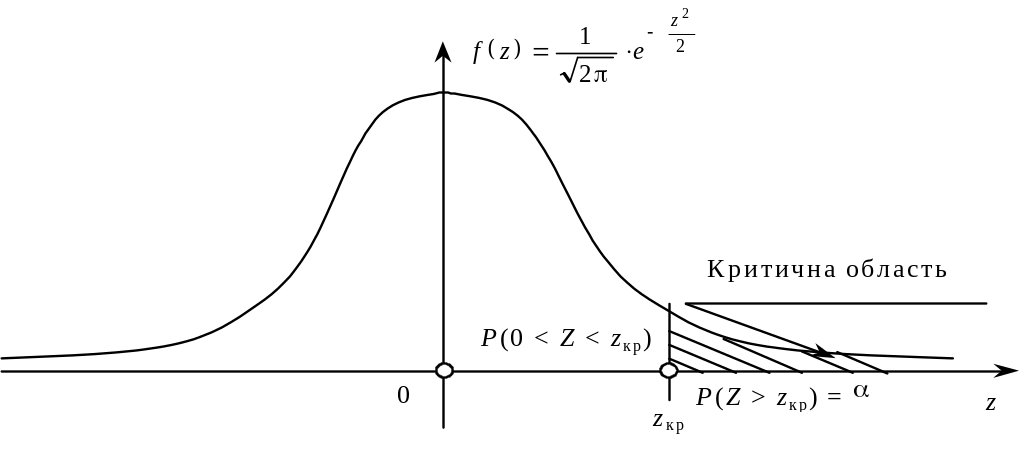
Правостороння критична область зображена на малюнку

2. Для того, щоб при заданому рівні значущості перевірити нульову гіпотезу при альтернативній гіпотезі потрібно обчислити спостережуване значення критерію за формулою (1) і за таблицею значень функції Лапласа знайти критичну точку лівосторонньої критичної області з рівняння . Враховуючи ту обставину, що функція Лапласа є непарною, за таблицею значень знаходимо аргумент і беремо його із знаком «мінус» . Якщо , то нульову гіпотезу приймають, якщо – відхиляють.

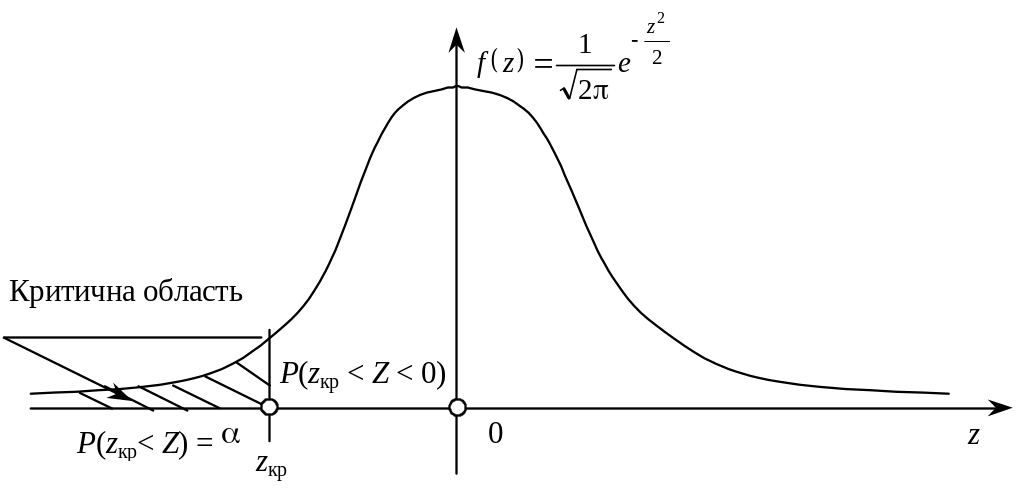
Лівостороння критична область зображена на малюнку

3. Для того, щоб при заданому рівні значущості перевірити нульову гіпотезу при альтернативній гіпотезі потрібно обчислити спостережуване значення критерію за формулою (1) і за таблицею значень функції Лапласа знайти критичну точку двосторонньої симетричної критичної області з рівняння . Якщо , то нульову гіпотезу приймають, якщо – відхиляють.

Двостороння критична область зображена на малюнку

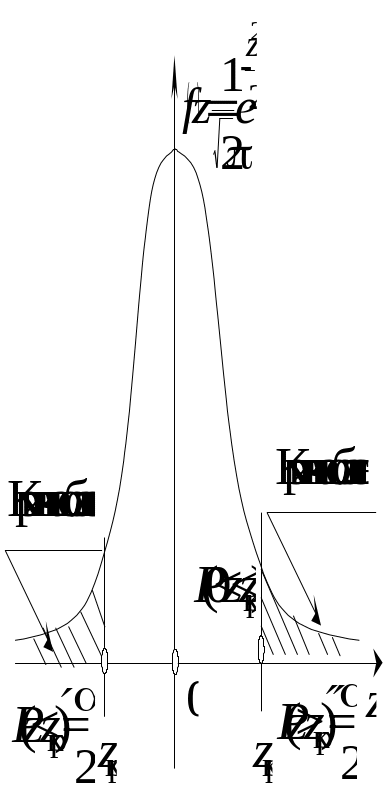
Припустимо, що дисперсія генеральної сукупності невідома. За критерій перевірки нульової гіпотези в цьому випадку візьмемо випадкову величину

,

де 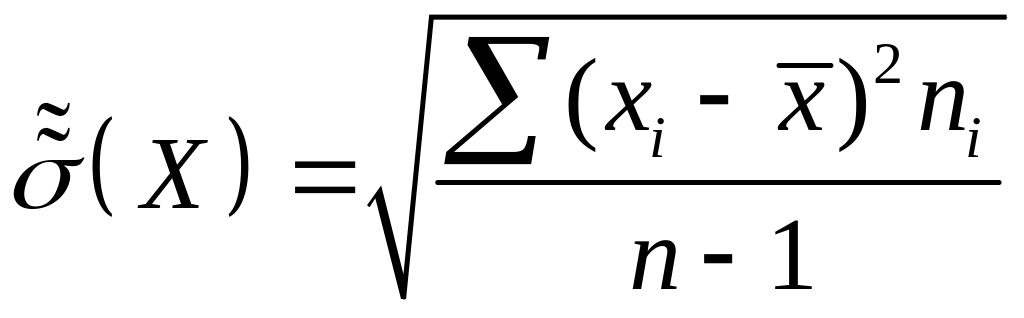– виправлене вибіркове середнє квадратичне відхилення. Ця величина розподілена за законом Стьюдента з ступенями вільності. Спостережуване значення критерію обчислюється за формулою

,

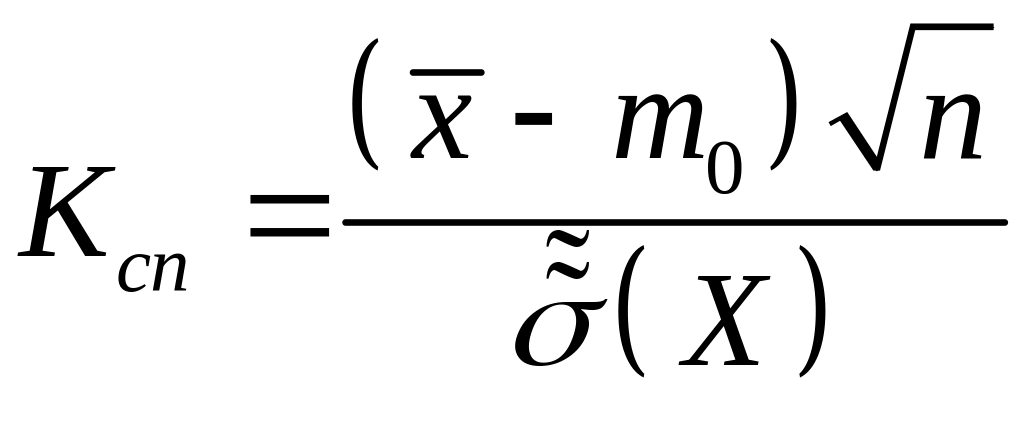а критичні точки у цьому разі визначаються за таблицею критичних точок розподілу Стьюдента за заданим рівнем значущості  та числом ступенів вільності .

Приклад 1. Розбіжність вимірів діаметрів кульок є випадковою величиною, яка має закон розподілу . При рівні значущості перевірити правильність мм, якщо альтернативна гіпотеза мм, коли відомо вибіркове середнє значення виміряних у 100 однотипних кульок мм.

Розв’язання. Оскільки мм, будується правостороння критична область. Для цього необхідно знайти критичну точку і побудувати правосторонню критичну область. Для знаходження критичної точки застосовуємо відомий вираз:

.

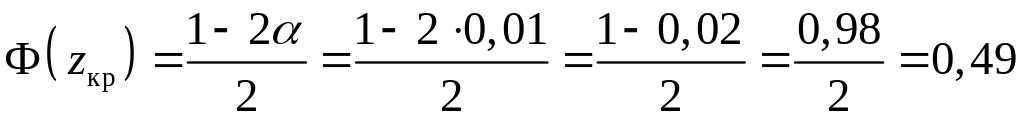За значенням і скориставшись таблицею знаходимо . Отже, правостороння критична область матиме вигляд, зображений на малюнку.

Обчислимо спостережуване значення критерію 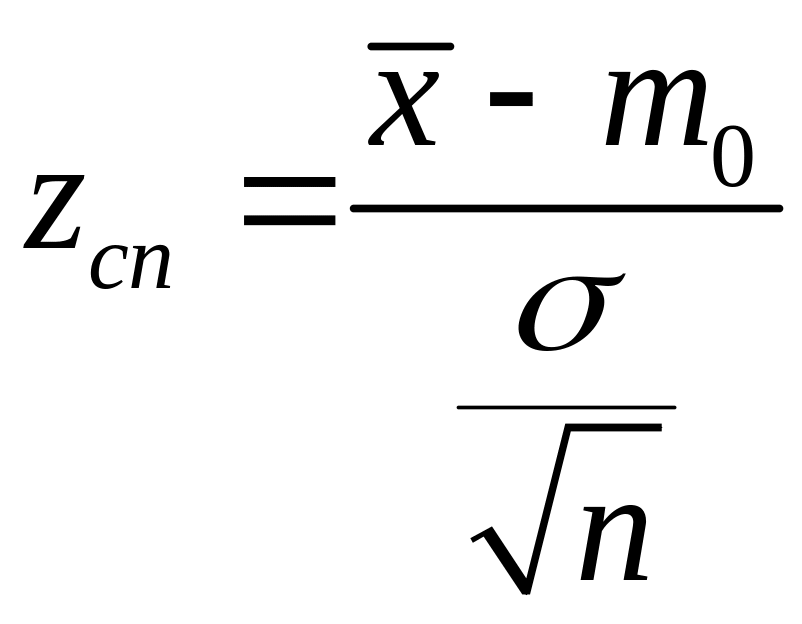. Оскільки мм, мм, мм, , маємо

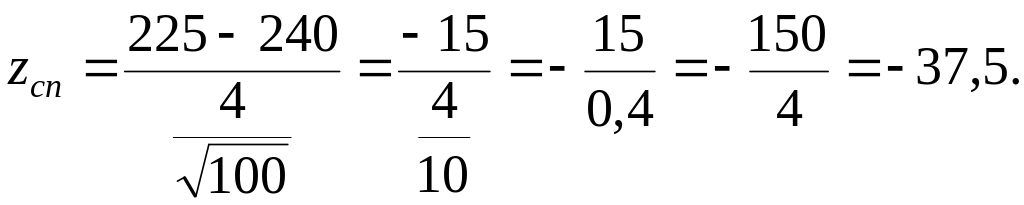
Висновок. Оскільки , то немає підстав для відхилення нульової гіпотези мм.

Отже, нульова гіпотеза приймається.

Приклад 2. Проведено 10 незалежних експериментів над випадковою величиною Х, що має нормальний закон розподілу з невідомими значеннями , . Наслідки експериментів подано у вигляді статистичного ряду:

xi	2,5	2	–2,3	1,9	–2,1	2,4	2,3	–2,5	1,5	–1,7
ni	1	1	1	1	1	1	1	1	1	1

При рівні значущості перевірити правильність нульової гіпотези , при альтернативній гіпотезі .

Розв’язання. Запишемо статистичний ряд у вигляді статистичного розподілу й обчислимо , :

xi	–2,5	–2,3	–2,1	–1,7	1,5	1,9	2	2,3	2,4	2,5
ni	1	1	1	1	1	1	1	1	1	1

.

.

.

.

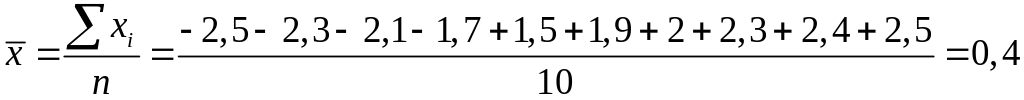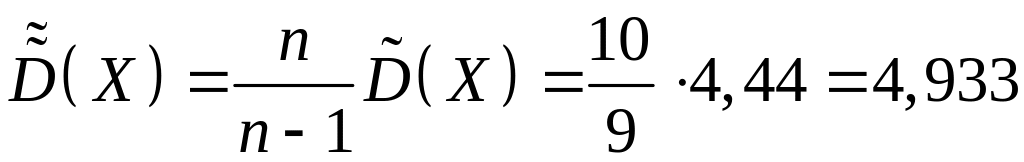При альтернативній гіпотезі будується лівостороння критична область. Для цього необхідно знайти критичну точку, застосовуючи статистичний критерій. За таблицею критичних точок розподілу Стьюдента знаходимо значення

= .

Оскільки щільність ймовірностей для розподілу Стьюдента є парною, то .

Критична область показана на малюнку

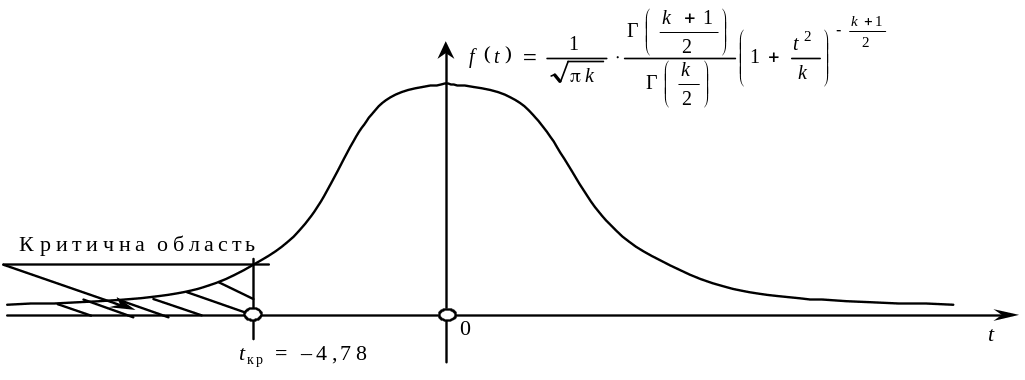
Обчислимо спостережуване значення критерію:

.

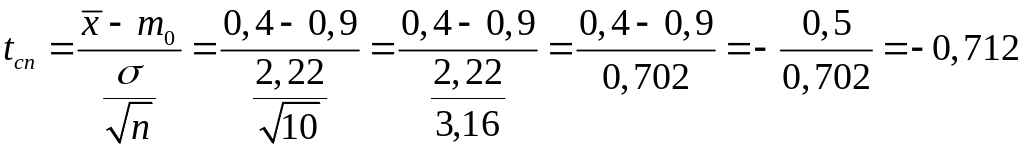Висновок. Оскільки , то немає підстав відхилити .