4. Лінійна регресія

Розглянемо випадок, який часто зустрічається на практиці: коли передбачувана залежність між випадковими величинами і є лінійною, тобто функція регресії на має вигляд:

.

Задача полягає в тому, щоб за результатами вибірки відшукати значення невідомих коефіцієнтів . Але істинні значення цих параметрів дістати неможливо, оскільки ми користуємося інформацією, здобутою від вибірки обмеженого об’єму. Тому знайдені значення параметрів будуть лише статистичними оцінками істинних (невідомих нам) параметрів . Якщо позначити вибіркові параметри через , лінійній моделі відповідатиме статистична оцінка

, (3)

яку ще називають емпіричною функцією регресії.

Скористуємось методом Гаусса. Утворимо суму квадратів відхилень

і підберемо коефіцієнти так, щоб

.

Для відшукання мінімуму візьмемо частинні похідні по і по і прирівняємо їх до 0:

;

.

Після елементарних перетворень отримаємо систему рівнянь:

Розв’язавши цю систему за правилом Крамера, дістанемо:

; (4)

. (5)

Підставивши отримані значення і в рівняння (3), будемо мати вибіркове рівняння регресії на .

Аналогічно розглядається регресія на :

Оцінки і параметрів і у вибірковому рівнянні регресії на

(6)

обчислюються за формулами:

; (7)

. (8)

Прямі і перетинаються в точці з координатами , причому кут між ними зменшується при збільшенні вибіркового коефіцієнта кореляції між випадковими величинами та Y. При обидві прямі збігаються.

Для контролю правильності обчислень використовують співвідношення

(9)

де – вибірковий коефіцієнт кореляції.

Параметри і можна також визначити з наступних формул

;

і тоді рівняння прямих регресії мають вигляд:

;

.

Коефіцієнти 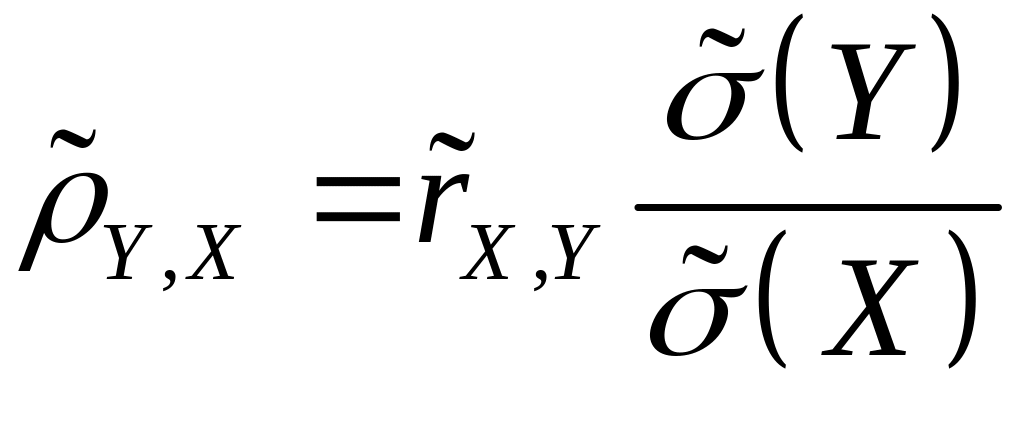і називаються коефіцієнтом регресії на та коефіцієнтом регресії на відповідно. Тоді рівняння прямих регресії можна записати у вигляді:

;

.

Якщо значення випадкової величини відомі без похибок, а значення випадкової величини незалежні та рівноточні, то середнє квадратичне відхилення (стандартна помилка) величин визначається за формулою

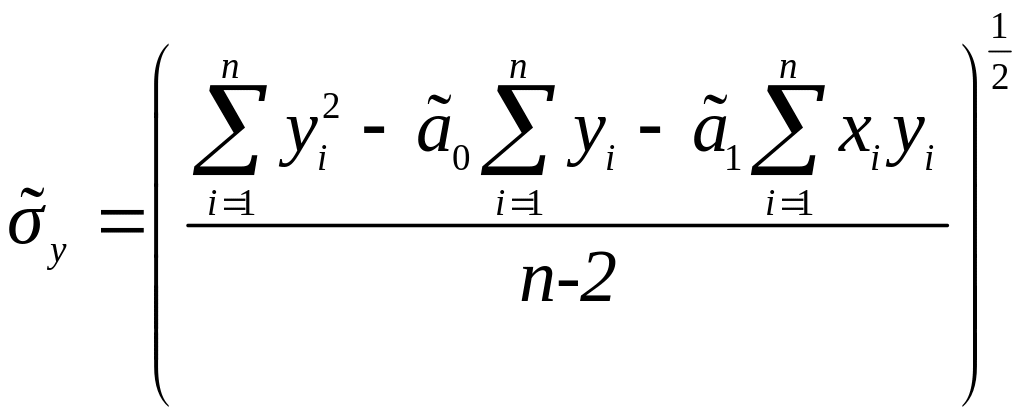, (10)

Оцінки дисперсій коефіцієнтів визначається за формулами

, . (11)

Якщо випадкова величина з має нормальний розподіл, то істинні значення коефіцієнтів лінійної регресії знаходяться в довірчому інтервалі:

, ( ) (12)

де , – оцінки, отримані методом найменших квадратів, а число знаходиться за таблицею розподілу Стьюдента при числі степенів вільності і рівні надійності , .

Приклад. Задані результати незалежних спостережень над системою випадкових величин :

	2	4	6	8	10
	4,5	7,0	8,0	7,5	9,0

Потрібно:

1) обчислити вибірковий коефіцієнт кореляції ;

2) побудувати кореляційне поле залежності ознаки від ;

3) припускаючи, що залежність між та близька до лінійної, визначити оцінки параметрів лінійної регресії на та на ;

4) нанести на кореляційне поле прямі регресії на та на .

5) визначити похибку вимірювань ;

6) знайти довірчі інтервали для істинних значень коефіцієнтів лінійної регресії на при .

Розв’язання: Побудуємо розрахункову таблицю:

№ з/п
1	2	4,5	4	20,25	9
2	4	7,0	16	49	28
3	6	8,0	36	64	48
4	8	7,5	64	56,25	60
5	10	9,0	100	81	90
	30	36	220	270,5	235

1) Обчислимо вибірковий коефіцієнт кореляції за формулою (2)

.

Коефіцієнт кореляції близький за своїм значенням до одиниці, отже, між та існує велика пряма залежність (вона є практично лінійною).

2) Побудуємо кореляційне поле:

3) З малюнка бачимо, що із збільшенням значень ознаки залежна змінна має тенденцію до збільшення. Тому припустимо, що залежність між ознаками та є лінійною, тобто функція регресії на має вигляд:

Визначимо оцінки параметрів лінійної регресії на за формулами (4) і (5):

;

.

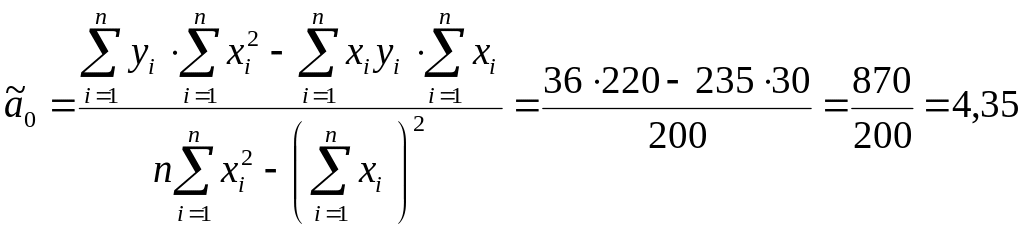Таким чином, вибіркове рівняння прямої регресії на має вигляд:

.

Визначимо тепер оцінки параметрів лінійної регресії на за формулами (6) і (7):

.

Таким чином, рівняння прямої регресії на має вигляд:

.

Перевіримо правильність обчислень за формулою (9)

що в точності збігається із вище обчисленим значенням .

4) Нанесемо на кореляційне поле прямі регресії на та на :

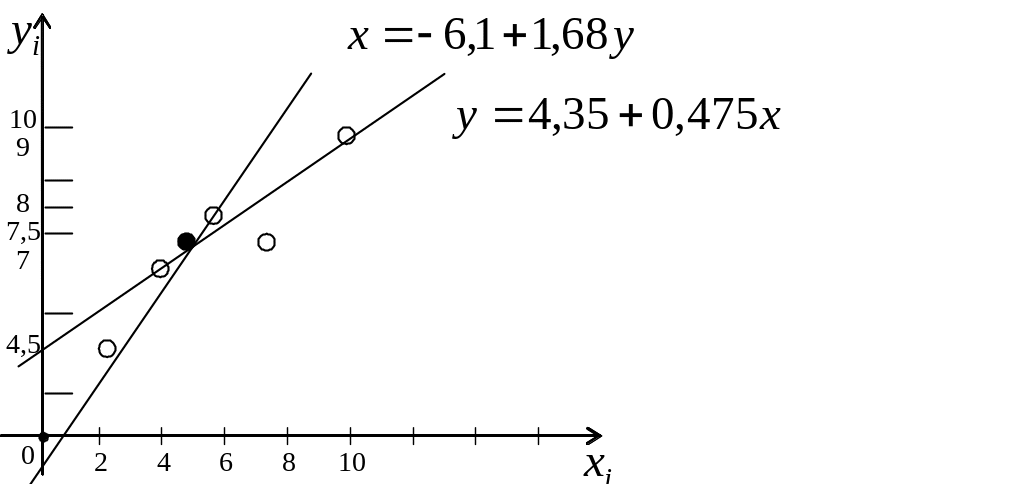
Прямі і перетинаються в точці з координатами .

5) Визначимо похибку вимірювань за формулою (10):

.

6) Знайдемо довірчі інтервали для істинних значень коефіцієнтів лінійної регресії на . Визначимо оцінки дисперсій коефіцієнтів і за формулами (11)

,

,

Звідки , .

З таблиці розподілу Стьюдента знаходимо . За формулами (12) визначимо довірчі межі для істинних значень коефіцієнтів і : ;

;

;

.

Таким чином, з довірчою ймовірністю інтервали

;

покривають істинні значення коефіцієнтів і .