2) Побудова довірчого інтервалу при невідомій дисперсії

Якщо дисперсія невідома, то її замінюють незміщеною оцінкою .

При заданій надійності довірчим інтервалом для оцінки математичного сподівання при невідомій дисперсії буде проміжок

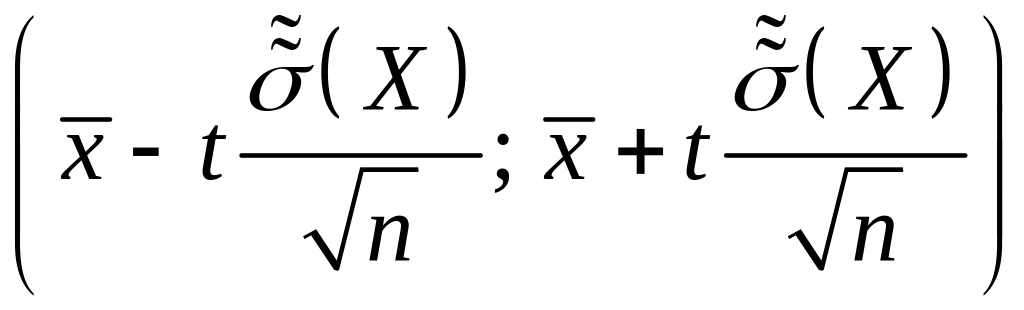
Число визначається з рівняння

,

де – щільність розподілу ймовірностей для закону Стьюдента ( -розподілу). Для відшукання складено спеціальні таблиці.

Приклад 9. Генеральна сукупність розподілена за нормальним законом з невідомою дисперсією. За вибіркою об’єму 10 знайдена вибіркова середня і виправлене вибіркове середнє квадратичне відхилення . Оцінити математичне сподівання при надійному рівні .

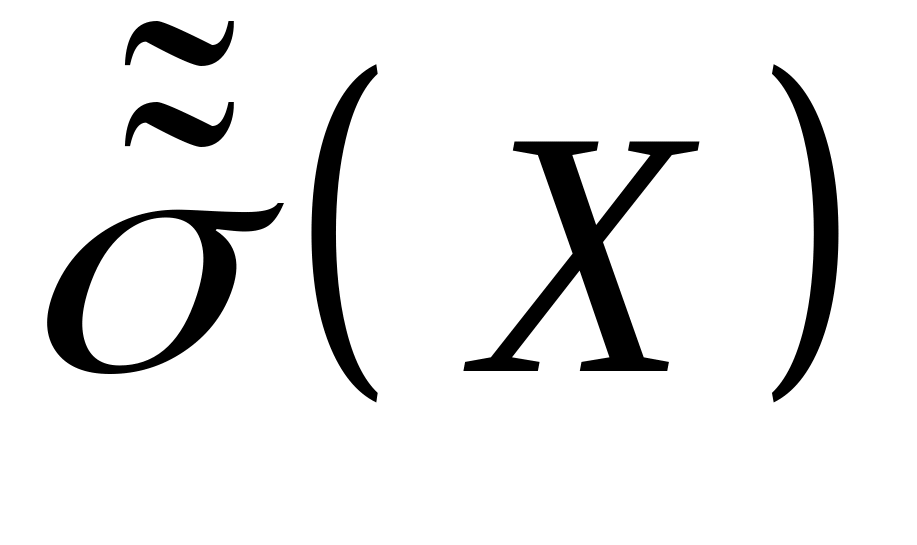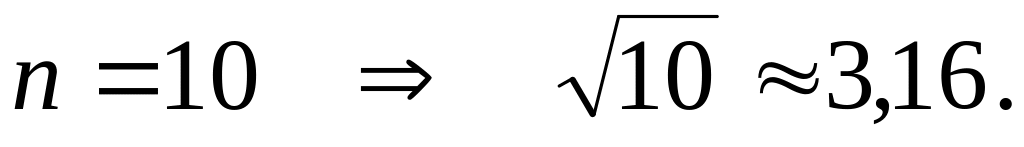Розв’язання. Для побудови довірчого інтервалу необхідно знати: , , . З умови задачі маємо: Величину знаходимо з таблиці: .

Знайдемо числові значення кінців довірчого інтервалу :

,

,

Таким чином, маємо:

.

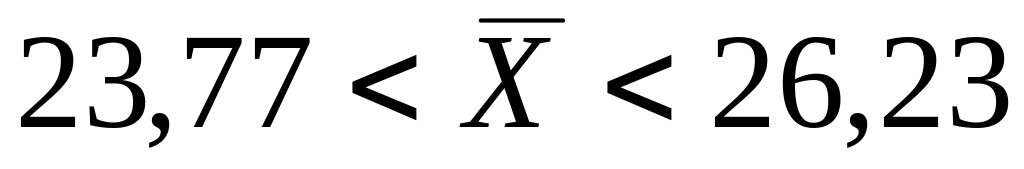Отже, з надійністю 0,99 (99% гарантії) інтервал покриває оцінюваний параметр .
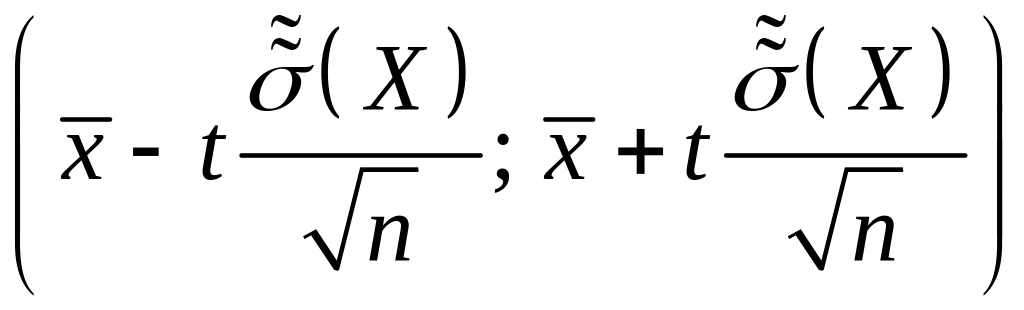