§ 8. Классификация пластин

Стандартной классификации пластин не существует. В строительной механике корабля применяется условная классификация пластин, которая позволяет упростить расчетные формулы. В зависимости от степени жесткости и действующих напряжений тонкие пластины классифицируются следующим образом:

абсолютно жесткие пластины, при изгибе которых цепные напряжения, возникающие под действием поперечной нагрузки, настолько малы, что ими можно пренебречь, т. е. суммарные напряжения в пластине  = _изг;

пластины конечной жесткости — влияние их цепных усилий на изгиб существенно и цепные напряжения соизмеримы с изгибными, а суммарные напряжения  = _изг + q;

гибкие пластины или мембраны, при изгибе которых цепные напряжения намного больше максимальных изгибных, поэтому изгибными можно пренебречь, а суммарные напряжения  = q.

Приведенная классификация относительна. Одна и та же пластина при неизменных условиях закрепления на опорном контуре в зависимости от значения нагрузки р может быть отнесена к любому из указанных выше классов.

Для пластины, имеющей определенную толщину и сравнительно малую нагрузку, возникающие цепные напряжения окажутся пренебрежимо малыми по сравнению с изгибными напряжениями, и пластина будет изгибаться как абсолютно жесткая. При дальнейшем увеличении нагрузки цепные напряжения возрастут и станут соизмеримыми с изгибными. Пластина будет изгибаться как пластина конечной жесткости. Наконец, при еще большем увеличении нагрузки цепные напряжения намного превзойдут изгибные, и пластина станет гибкой. Вопрос о том, к какому классу следует отнести ту или иную пластину, решается с учетом размеров пластины, вида опорного контура и значений действующей нагрузки.

Гибкие пластины в составе судового корпуса практически не встречаются, поэтому в дальнейшем все расчетные формулы и методики расчета будут приводиться для жестких пластин. Методика определения класса пластин рассмотрена при исследовании изгиба пластин конечной жесткости.

§ 9. Расчет абсолютно жестких пластин

Изгиб пластин, гнущихся по цилиндрической поверхности. Многие пластины судового корпуса работают как абсолютно жесткие и имеют вид удлиненного прямоугольника. Если отношение сторон а/b > 2, то с достаточной для практики точностью изгиб такой пластины под действием равномерно распределенной поперечной нагрузки можно считать цилиндрическим. В этом случае на большей части длины пластина прогибается одинаково, и лишь на небольших участках в районе коротких сторон опорного контура прогибы пластины изменяются по длине (рис. 2.2, а).

Для пластины, гнущейся по цилиндрической поверхности, достаточно рассчитать мысленно выделенную из ее средней части балку-полоску единичной ширины (1 см) с прямоугольным поперечным сечением F = s1 = s (рис. 2.2, б).

Термин «балка-полоска» был введен в строительную механику корабля И. Г. Бубновым, который разработал теорию сложного изгиба балок и распространил результаты этой теории на изгиб пластин, гнущихся по цилиндрической поверхности.

Рис. 2.2. К расчету пластин, гнущихся по цилиндрической поверхности: а — расчетная схема пластины; б — балка-полоска и ее сечение.

Поперечное сечение балки во время изгиба искажается (рис. 2.3). В отличие от обычной балки изгиб балки-полоски не сопровождается искажением поперечного сечения, так как этому препятствуют соседние балки-полоски. Следовательно, прямоугольное сечение в процессе изгиба остается прямоугольным.

Если бы рассматриваемая балка-полоска изгибалась независимо от остальных частей пластины, то для исследования ее изгиба были применимы ранее выведенные формулы при условии, что в них I = bs³/12 = = 1s³/12. Если же балка-полоска изгибается в составе пластины, то условия изгиба изменяются лишь вследствие того, что ее поперечное сечение не может деформироваться в направлении оси оу.

Таким образом, в случае изгиба изолированной балки-полоски (или обычной балки) _у = 0; _у  0, а в случае изгиба балки-полоски, входящей в состав пластины, _у  0, _y = 0.

Согласно закону Гука связь между напряжениями и деформациями балки-полоски, входящей в состав пластины, определяется формулами

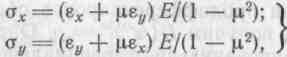(2.1)

где _х и _y — нормальные напряжения по осям соответственно х и у; _х и _у — относительные удлинения по осям соответственно х и у.

Для обычной балки (или изолированной балки-полоски) _y = 0 и, следовательно, _у = –_х. Подставляя выражение _y в первое уравнение (2.1), получим для обычной балки _х = Е_х. Применительно к балке-полоске, входящей в состав толщины _y = 0 и, следовательно, _x = _хЕ/(1 – ²).

Рис. 2.3. Искажение прямоугольного сечения при изгибе балки.

Сопоставляя формулы, связывающие нормальные напряжения вдоль оси балки с удлинением в направлении этой оси, видим их сходство. Различаются же они тем, что для балки-полоски вместо модуля нормальной упругости Е принята величина E/(1 – ²), называемая приведенным модулем нормальной упругости.

Используя дифференциальное уравнение изгиба балок EIw" = М, получаем дифференциальное уравнение изгиба балки-полоски

(2.2)

где величина Es³/12(1 — ²) = D — цилиндрическая жесткость пластины; w" — вторая производная по х прогиба балки-полоски. Формулу (2.2) можно записать в следующем виде:

(2.3)

Дифференциальное уравнение изгиба балки-полоски, вырезанной из пластины, изгибающейся по цилиндрической поверхности, отличается от обычного дифференциального уравнения изгиба балки только тем, что:

изгибающий момент М относится к единице ширины сечения (размерность силы);

в качестве момента инерции I выступает момент инерции единицы ширины сечения пластины s³/12;

роль модуля нормальной упругости (модуля Юнга) принимает на себя величина Е₁ =Е/(1 — ²);

при ширине балки-полоски, равной 1 см, интенсивность поперечной нагрузки q, приходящаяся на единицу длины, равна интенсивности распределенной нагрузки р (давлению) на пластину.

Использовав из теории изгиба балок зависимости dM/dx = N; d²M/dx² = q и продифференцировав обе части уравнения (2.3) дважды по х, получим D(w")" = р. Определение прогиба w сводится к интегрированию дифференциального уравнения при заданных граничных условиях. Вычислив прогиб, можно найти изгибающий момент и нормальные напряжения. Воспользовавшись формулой (1.3) для определения нормальных напряжений балок при изгибе и подставив значение момента сопротивления поперечного сечения балки-полоски W = I/0,5s = s²/6, получим формулу для наибольших нормальных напряжений в крайних волокнах балки-полоски

(2.4)

Касательные напряжения, вызванные перерезывающими силами, при цилиндрическом изгибе пластин оказываются малыми, и их обычно не вычисляют.

В практических расчетах пластин, гнущихся по цилиндрической поверхности, широко используют таблицы элементов изгиба статически определимых и статически неопределимых балок [20, т. 1]. При этом ограничиваются определением наибольших значений прогибов и изгибающих моментов. В формулах для вычисления прогиба и изгибающего момента заменяют жесткость на изгиб EI цилиндрической жесткостью D, интенсивность равномерно распределенной нагрузки q — интенсивностью нагрузки на пластину р, а длину балки l — длиной короткой стороны пластины b. В результате получают значения прогиба и изгибающего момента для пластины.

Рассматривая цилиндрический изгиб пластины, исключающий влияние коротких сторон опорного контура, предполагают, что пластина имеет бесконечно большую длину. При конечной длине пластины короткие стороны опорного контура всегда оказывают благоприятное влияние на условия изгиба, т. е. при небольшом отношении сторон пластины наибольшие прогибы и напряжения всегда меньше, чем в балке-полоске.

В составе судового корпуса имеются пластины, отношение сторон опорного контура которых меньше двух [a/b)<2]. При расчете таких пластин по приведенным выше формулам получают погрешность в безопасную сторону. Для прикидочных расчетов пластин указанные формулы вполне пригодны.

Рис. 2.4. Расчетные схемы общего изгиб абсолютно жестких пластин: а — свободно опертой; б — жестко заделанной.

Общий случай изгиба абсолютно жестких пластин. В практике расчетов абсолютно жестких пластин широко применяют приближенные расчетные формулы с использованием таблиц, составленных на основании теоретических решений. Обычно определяют только прогибы и изгибающие моменты. При этом расчетная формула проверки прочности пластины имеет вид

В настоящем учебнике приведены формулы (без выводов) для случаев изгиба пластин, наиболее часто встречающихся в практике расчетов.

Пластина свободно оперта по всем четырем кромкам рис.2.4, а). Обозначения: M₁ и М₂ — изгибающие моменты в центре пластины, в сечениях, параллельных соответственно короткой и длинной сторонам пластины. Остальные обозначения указаны в § 7. Расчетные формулы:

(2.5)

Числовые значения коэффициентов k₁, k₂, k₃ приведены в зависимости от отношения сторон а/b в табл. 2.1 [20, т. 2].

Пластина жестко заделана на опорном контуре по всем четырем кромкам (рис. 2.4,6). Обозначения: М'₁ и М'₂ — наибольшие изгибающие моменты соответственно посредине короткой и длинной сторон опорного контура. Остальные обозначения те же, что и для свободно опертой пластины. Расчетные формулы:

(2.6)

Числовые значения коэффициентов k_i приведены в зависимости от отношения сторон a/b в табл. 2.2 [20, т. 2].

Таблица 2.1. Численные значения коэффициентов k_i при расчете пластин, свободно опертых по всему контуру

a/b	k1	k2	k3	k4	k5	k6	k7	k8	k9	k10
1,0	0,0443	0,0479	0,0479	0,338	0,338	0,420	0,420	0,065	0,250	0,250
1,1	0,0530	0,0494	0,0553	0,346	0,360	0,440	0,440	0,064	—	—
1,2	0,0616	0,0501	0,0626	0,352	0,380	0,450	0,455	0,062	0,260	0,285
1,3	0,0697	0,0504	0,0693	0,357	0,397	0,465	0,468	0,061	—	—
1,4	0,0770	0,0506	0,0753	0,361	0,411	0,470	0,478	0,059	0,265	0,310
1,5	0,0843	0,0500	0,0812	0,363	0,424	0,485	0,486	0,057	—	—
1,6	0,0906	0,0493	0,0862	0,366	0,435	0,485	0,491	0,054	0,267	0,332
1,7	0,0964	0,0486	0,0908	0,367	0,444	0,488	0,496	0,052	—	—
1,8	0,1017	0,0479	0,0948	0,368	0,452	0,491	0,491	0,050	0,271	0,347
1,9	0,1064	0,0471	0,0985	0,369	0,459	0,494	0,502	0,048	—	—
2,0	0,1106	0,0464	0,1017	0,370	0,465	0,496	0,503	0,046	0,272	0,364
3,0	0,1336	0,0404	0,1185	0,371	0,493	0,498	0,505	0,031	0,272	0,410
4,0	0,1400	0,0384	0,1235	0,371	0,498	0,500	0,502	0,024	0,272	0,435
5,0	0,1416	0,0375	0,1246	0,371	0,500	0,500	0,500	0,019	0,272	0,452
	0,1422	0,0375	0,1250	0,371	0,500	0,500	0,500	0	0,272	0,500

Таблица 2.2. Численные значения коэффициентов ki при расчете пластин, жестко заделанных по всему контуру

а/b	k1	k2	k3	k4	k5	k6	k7	k8	k9	k10	k11
1,0	0,0138	0,0229	0,0229	0,0513	0,0517	0,452	0,452	0,440	0,440	0,250	0,250
1,1	0,0165	0,0234	0,0264	0,0538	0,0554	0,412	0,448	0,450	0,473	0,253	0,271
1,2	0,0191	0,0231	0,0299	0,0554	0,0612	0,381	0,471	0,457	0,493	0,255	0,290
1,3	0,0210	0,0224	0,0327	0,0563	0,0668	0,352	0,491	0,462	0,505	0,256	0,306
1,4	0,0227	0,0215	0,0340	0,0568	0,0714	0,327	0,505	0,464	0,510	0,256	0,320
1,5	0,0241	0,0204	0,0368	—	0,0753	0,305	0,517	0,465	0,515	0,255	0,332
1,6	0,0251	0,0193	0,0381	0,0571	0,0784	—	—	0,465	0,518	0,255	0,343
1,7	0,0260	0,0182	0,0342	0,0571	0,0807	—	—	0,465	0,519	0,254	0,352
1,8	0,0267	0,0174	0,0401	0,0571	0,0821	—	—	0,465	0,520	0,253	0,360
1,9	0,0272	0,0165	0,0407	0,0571	0,0826	—	—	0,465	0,518	0,252	0,367
2,0	0,0276	—	—	0,0571	0,0829	—	—	0,465	0,515	0,252	0,374
3,0	0,0279	—	—	0,0571	0,0832	—	—	0,465	0,510	0,251	0,412
4,0	0,0282	—	—	0,0571	0,0833	—	—	0,465	0,505	0,251	0,432
5,0	0,0284	—	—	0,0571	0,0833	—	—	0,465	0,505	0,250	0,450
оо	0,0284	—	—	0,0571	0,0833	—	—	0,465	0,505	0,250	0,500