§ 6. Устойчивость стержней

Важным фактором, определяющим возможность эксплуатации любого инженерного сооружения в заданных условиях, является устойчивость его конструктивных элементов. В составе судового корпуса имеется ряд связей, которые подвергаются действию сжимающих нагрузок, способных вызвать потерю устойчивости (т. е. их выпучивание). Например, при плавании судна на подошве волны сжатыми оказываются продольные связи верхних палуб, а при плавании на вершине волны — продольные связи днища. Потеря устойчивости основных связей может привести к серьезным нарушениям прочности судового корпуса, а в ряде случаев и к гибели судов. Для ряда элементов конструкций корпуса судна устойчивость является условием, определяющим их размеры (продольные балки палубного набора, пиллерсы, распорки и т. д.).

Из курса технической механики известно, что возможны три состояния равновесия системы:

1) устойчивое, когда система, мало отклоненная от состояния равновесия под действием приложенной нагрузки, после удаления этой нагрузки, снова возвращается в состояние равновесия;

2) неустойчивое, когда при тех же условиях система не возвращается в состояние равновесия, а стремится еще более отклониться от него;

3) безразличное, когда при тех же условиях система не возвращается в состояние равновесия и не стремится увеличить отклонение, т. е. система имеет бесконечно много положений равновесия.

Особенность упругих систем состоит в том, что при изменении действующих на них определенных нагрузок, они могут переходить из одного состояния равновесия в другое.

Проектируемые конструкции должны находиться в состоянии устойчивого равновесия. Статической устойчивостью называется устойчивость под действием нагрузок, возрастающих относительно медленно.

Еще во второй половине XVIII в. Эйлер разработал некоторые основные вопросы упругой устойчивости. Однако решения, которые были им получены, до конца XIX в. не входили в практику расчетов, так как они были выполнены для стержней, которые теряют устойчивость при нагрузках, лежащих в пределах пропорциональности, т. е. применимости закона Гука.

Нагрузка, при которой равновесие системы становится безразличным по отношению к одному из возможных малых ее отклонений, называется критической. Условимся называть эйлеровой Р_э — критическую нагрузку упругих систем, вычисленную в предположении о применимости закона Гука, а критической нагрузкой Р_кр — истинное значение этой нагрузки, определенное с учетом отклонения от закона Гука. Те же понятия

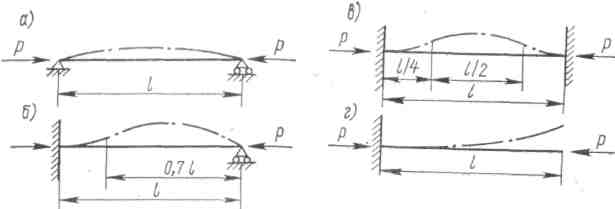
Рис. 1.19. Случаи закрепления концов стержня на опорах при сжатии: а — свободно опертые концы; б — один конец жестко заделан, другой — свободно оперт; в — жестко заделаны оба конца; г — один конец жестко заделан, другой свободный.

отнесем и к напряжениям

(1.9)

Формулы эйлеровых нагрузок и напряжений имеют вид

(1.10)

где F — площадь поперечного сечения стержня с присоединенным пояском; l — минимальный момент инерции стержня с присоединенным пояском; l — приведенная длина стержня — расстояние между точками перегиба на кривой потери устойчивости; . — коэффициент приведения. Если учесть, что ² = I/F, где  — радиус инерции сечения, и обозначить  = l/, то получим _э = ²E/², где  — относительная гибкость стержня.

Формулы Эйлера справедливы только в пределах пропорциональности, т. е. _э  _пц, поэтому ими можно пользоваться только при расчете устойчивости стержней с относительной гибкостью

где (_пц — предел пропорциональности материала. Так, если для углеродистой стали принять _пц  196 МПа, E = 210⁵ МПа то

т. е. для стержня из углеродистой стали теоретические формулы эйлеровых напряжений и нагрузок справедливы при   100.

Эйлером были определены значения критической нагрузки для различных случаев закрепления стержней (рис, 1.19):

I случай (рис. 1.19, a),  = 1,0

II случай (рис. 1.19, б),  = 0,7

III случай (рис. 1.19, в),  = 0,5

IV случай (рис. 1.19, г),  = 2,0

Однако в судовых конструкциях относительная гибкость стержней обычно значительно меньше 100, и поэтому теоретические формулы, основанные на использовании закона Гука, не применимы. В конце XIX в. были предложены различные формулы для определения критических напряжений за пределом пропорциональности, основанные на опытных данных. Для таких стержней используют выражения

(1.11)

где  — коэффициент, учитывающий влияние отступления от закона Гука на устойчивость.

С целью практического определения критической нагрузки и критических напряжений в судостроительных расчетах в настоящее время применяют обобщенные кривые, построенные по экспериментальным данным [20, т. 3]. На основании этих кривых для удобства пользования составлена табл. 1.2 зависи

Таблица 1.2. Значения коэффициента  в зависимости от отношения _э/_т

э/т		э/т		э/т	
0,50	1,000	1,20	0,721	1,90	0,515
0,55	0,982	1,25	0,706	1,95	0,504
0,60	0,962	1,30	0,691	2,00	0,490
0,65	0,942	1,35	0,676	2,05	0,480
0,70	0,920	1,40	0,660	2,10	0,470
0,75	0,900	1,45	0,645	2,15	0,460
0,80	0378	1,50	0,628	2,20	0,450
0,85	0,858	1,55	0,609	2,25	0,442
0,90	0,840	1,60	0,593	2,30	0,433
0,95	0,820	1,65	0,578	2,35	0,424
1,00	0,800	1,70	0,563	2,40	0,416
1,05	0,780	1,75	0,549	2,45	0,408
1,10	0,760	1,80	0,535	2,50	0,400
1,15	0,740	1,85	0,525	2,55	0,392

мости коэффициента  от отношения _э/_т. Из указанной работы видно, что при

Критические напряжения всегда должны быть больше сжимающих, но не более _т

Если по заданным геометрическим элементам поперечного сечения и длине стержня необходимо определить критическую силу, то задачу решают в такой последовательности: находят Р_э и _э, затем по таблице определяют ; далее вычисляют

_кр = _э и Р_кр = _крF.

Для подбора сечения стержня, обеспечивающего заданную устойчивость, следует: по заданной величине _кр согласно графику [20, т. 3, с. 230] установить _э; далее, пользуясь формулой _э = ²EI/(l)²F, определить отношение I/F и методом подбора найти F и I для стержня с присоединенным пояском.

Вопросы для повторения

1. Назовите правило знаков, принятое в строительной механике морских судов.

2. Как распределяются нормальные и касательные напряжения по высоте сечения балки при изгибе? По каким формулам их определяют?

3. Объясните методику подбора профиля балки по _доп и внешней нагрузке.

4. Назовите требования, предъявляемые к профилю балок набора.

5. Охарактеризуйте статически неопределимые балки и изложите последовательность раскрытия статической неопределимости однопролетных балок.

6. Расскажите о последовательности раскрытия статической неопределимости многопролетных балок и порядке построения эпюр М и N.

7. Назовите методы раскрытия статической неопределимости простых рам и простейших перекрытий.

8. Что такое устойчивость стержней? Какие бывают состояния равновесия упругих систем?

9. Для каких стержней справедливы формулы Эйлера? Назовите условия обеспечения устойчивости.