§ 2. Подбор поперечного сечения балок

Характеристики профилей, работающих на изгиб. Сечение балки, работающей на изгиб, должно воспринимать изгибающий момент и перерезывающую силу. Для обеспечения прочности при работе профиля на срез необходимо знать определенную площадь сечения стенки, а при работе на изгиб — ее распределение по высоте сечения. Задача о подборе профиля с требуемым моментом сопротивления не имеет однозначного решения. Обычно критерием рациональности при подборе элементов профиля требуемой прочности считают минимум расчетного поперечного сечения балки, т. е. минимум ее массы.

Наиболее выгодное распределение материала в сечении профиля, работающего на изгиб, — сосредоточение его в двух параллельных равных поясках, расположенных на определенном расстоянии один от другого (h = 2z). Такой профиль называют идеальным. Момент его сопротивления W = |z|F = 0,5hF. Для восприятия перерезывающей силы и просто для вовлечения в совместную работу поясков необходимо часть материала выделить на стенку профиля. Поэтому любой реальный профиль, площадь сечения которого одинакова с идеальным профилем, имеет меньший момент сопротивления W = 0,5hF, где  < 1,0 — коэффициент утилизации сечения, предложенный И. Г. Бубновым. Однако, сопоставляя профили с одинаковой площадью сечения F, но различной высоты h, можно увидеть, что не всегда большее значение  дает и большее значение W.

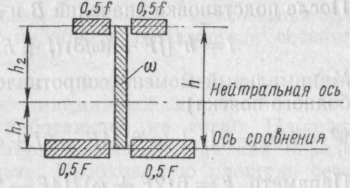
Рис. 1.8. Элементы составного таврового профиля. f и F — площади сечения меньшего большего поясков.

Более объективной характеристикой использования материала в сечении профиля является так называемая удельная площадь по моменту сопротивления C_w = F₀/W^2/3 и по моменту инерции C_i = F₀/I^1/2. Для профилей, присоединяемых к обшивке, F₀ — площадь сечения собственно профиля; W и I — момент сопротивления и момент инерции профиля с присоединенным пояском обшивки. Профиль будет тем выгоднее, чем меньше его удельная площадь.

Для геометрически подобных профилей коэффициенты удельной площади примерно одинаковы. Например, у полособульбов, приваренных к обшивке, С_w  0,650,67 в зависимости от градации профиля в сортаменте (группы «а» и «б»). У тавровых балок с присоединенным пояском C_w  0,500,55 и т. д. Чем меньше значение С_w, тем при прочих равных условиях профиль выгоднее.

Моменты сопротивления составного профиля. Чтобы исследовать зависимость момента сопротивления профиля от его элементов, рассмотрим несимметричный двутавровый профиль из однородного материала с элементами (рис. 1.8): f — площадь сечения меньшего пояска; F — площадь сечения большего пояска;  — площадь сечения стенки; h — высота балки между ЦТ поясков. Предполагая, что толщина поясков мала по сравнению с высотой профиля, можно пренебречь значениями собственных моментов инерции поясков.

Найдем зависимость минимального момента сопротивления сечения профиля (на уровне свободного — меньшего пояска) от элементов сечения. Примем ось сравнения проходящей через ЦТ большего пояска параллельно его поверхности (см. рис. 1.8). Площадь поперечного сечения профиля A = f + F + . Статический момент площади относительно оси сравнения В = fh + 0,5h. Отстояние нейтральной оси от оси сравнения

Отстояние меньшего пояска от нейтральной оси

Момент инерции сечения относительно нейтральной оси

После подстановки значений В и А получим

I = h² [fF + (/3) (f + F + /4)]/(f + F + ).

Минимальный момент сопротивления профиля (на уровне свободного пояска)

W = I/h₂ =h[f + (/6) (4F – 2f + )/(2F + )] = h (f + /k). (1.7)

Параметр k = 6(2F + )/(4 — 2f + ). Формула (1.7) была предложена И. Г. Бубновым.

Для анализа зависимости момента сопротивления профиля от элементов его сечения Н. В. Маттес ввела параметр , характеризующий положение нейтральной оси сечения:  = = h₁lh₂ = (2f + )/(2F + ) < 1,0. Поскольку (4F – 2f + )/(2F + ) = 2 – , то формулу (1.7) представим в виде

(1.8)

а формулу момента инерции относительно нейтральной оси — в упрощенном виде

Сравнивая формулы (1.7) и (1.8), видим, что k = 6/(2—). Для симметричного двутавра площади поясков равны, т. е. f = F;  = 1,0 и k = 6. В случае, когда один поясок намного больше другого (F >> f),   0 и k  3. Следовательно, в формуле (1.7) параметр k в зависимости от соотношения площади поясков изменяется в пределах 3 < k  6.

Минимальный момент сопротивления несимметричного двутавра, как видно из формулы (1.7), в наибольшей степени зависит от высоты профиля h и площади меньшего пояска f. При необходимости увеличить W до требуемого значения в первую очередь следует это сделать за счет пропорционального увеличения h или соответствующего увеличения f, либо за счет увеличения h и f одновременно. В этих случаях потребуется минимальное количество материала для увеличения сечения балки. Увеличение площади сечения стенки  в несколько раз менее эффективно, чем увеличение площади меньшего пояска. Изменение площади большего (присоединенного) пояска мало влияет на изменение минимального момента сопротивления составного профиля.

По необходимому моменту сопротивления поперечного сечения балки с присоединенным пояском выбирается ближайший по сортаменту профиль симметричного или несимметричного полособульба, у которого момент сопротивления с условным присоединенным пояском больше или равен требуемому (см. табл. 1 и 2 приложения). Если в сортаменте отсутствует момент сопротивления профиля с условным присоединенным пояском, то профиль можно подобрать по площади сечения, используя зависимость F₀ = C_wW^2/3.

Подбор составного таврового профиля. Задача подбора составного таврового профиля минимальной массы появляется при проектировании балки, работающей на изгиб. Площадь присоединенного пояска считается известной, так как определяется требованиями к обшивке. Необходимую площадь сечения стенки балки из условия прочности на срез вычисляют по формуле (1.5). Толщину стенки принимают не менее минимально допустимой с учетом интенсивности коррозии, срока службы (s_с  s_min). Отношение высоты стенки к ее толщине, должно удовлетворять условию устойчивости.

Если определяющим для толщины стенки является требование минимальной толщины, то, получив из формулы (1.7) площадь сечения балки F₀ = f +  в зависимости от необходимого момента сопротивления, найдем минимальную площадь по условию экстремальности (dF₀/dh = 0). В результате высота балки при k = 4,5 оказывается равной . Получив предварительную высоту балки, необходимо проверить устойчивость ее стенки.

Если определяющим для толщины стенки будет требование устойчивости s_c  h/m, то аналогичное условие экстремума при k = 4,5 приведет к высоте балки h_oрт  0,88 , где т нормируется в зависимости от значения расчетных нормальных и касательных напряжений.

Поскольку в районе экстремумов функция изменяется медленно, даже большое отклонение проектной высоты от оптимальной не вызовет значительного утяжеления профиля.

После выбора высоты профиля и площади стенки необходимо определить площадь свободного пояска f. Для этого воспользуемся формулой (1.7), откуда f = W/h – /k. Значение k в первом приближении можно принять равным 4,5. Далее, после окончательного выбора площади свободного пояска, уточняют значение k [см. формулу (1.7)].

Определив площадь свободного пояска f, следует выбрать его ширину b и толщину s_п. При этом необходимо обеспечить выполнение условий устойчивости пояска как пластины, а также учесть практические соображения, связанные с коррозионным износом, технологичностью и т. д. Ширина свободного пояска рамной балки (в мм), измеренная от ее стенки, должна быть не более определенной по формуле

где s_п — толщина свободного пояска, мм. Толщину свободного пояска желательно принимать на 2—3 мм больше, чем толщина стенки, но не более утроенной толщины стенки у рамных балок.

Рис. 1.9. Сечение тавровой балки с присоединенным пояском (к примеру расчета) .

После подбора профиля проверочный расчет момента сопротивления и момента инерции составного профиля выполняют в табличной форме.

Пример. Определить момент инерции и момент сопротивления составного таврового профиля (рис. 1.9). Для упрощения ось сравнения принимаем посередине толщины присоединенного пояска. Расчет выполняем в форме табл. 1.1.

Таблица 1.1. Вычисление момента инерции и моментов сопротивления тавровых профилей

Номер связи	Наименование связи	Размеры, мм	Площадь F, см2	Отстояние ЦТ связи от оси сравнения z, см	Статический момент площади связи относительно оси сравнения Fz, см3	Моменты инерции, см4
						Собственный i	Переносный Fz2
1	2	3	4	5	6	7	8
1 2 3	Присоединенный поясок Стенка Свободный поясок	8х600 6х350 10х140	48 21 14	0 17,9 35,9	0 375 503	2140	0 6729 18 041
Сумма		—	А = 83	—	В = 878	С = 26 910

Собственный момент инерции стенки (связь 2) i = s_ch³/12 = 0,635³/12 = 2140 см⁴. Собственными моментами инерции связей 1 и 3 пренебрегаем ввиду их малости.

Отстояние нейтральной оси от оси сравнения e = В/А = 878/83 = 10,6 см. Момент инерции относительно нейтральной оси I = С – е²А = 26 910 – 10,6²-83 = 17 580 см⁴.

Отстояние от оси сравнения крайних волокон: присоединенного пояска h₁ = е + s/2 = 10,6 + 0,4 = 11,0 см; свободного пояска h₂ = s + h + s_п – h₁ = 0,8 + 35 + 1,0 – 11,0 = 25,8 см.

Момент сопротивления крайних волокон: присоединенного пояска W₁ = I/h₁ = 17 580/11 = 1600 см³; свободного пояска W₂ = I/h₂= 17 580/25,8= 681 см³. Минимальный момент сопротивления — W₂.

Вычислим W_min по формуле (1.7)

k = 6(2  48 + 21)/(448–214 + 21) = 3,79; W_min = 35(14 + 21/3,79) = 684 см³.

Из сопоставления результатов расчета W_min в форме таблицы и по формуле (1.7) видно, что разница между ними незначительная (до 3 %).