Групування.

Групування даних - розподіл чи об’єднання одиниць сукупності у групи за певними істотними для них ознаками. Групування - це один з методів зведення, який забезпечує узагальнення даних, подання їх у компактному, узагальненому вигляді, метод, який створює основу для наступного зведення і аналізу даних.

Для проведення групування необхідно:

1) визначити типи явищ, які повинні бути виділені та зіставити з видом групування;

2) вибрати ознаки групування, які формують опис типів;

3) встановити границі інтервалів зміни ознак;

4) оформити групування у вигляді таблиці.

Групування бувають:

• типологічні;

• структурні;

• аналітичні.

Типологічне групування – це розподіл досліджуваної якісно різнорідної сукупності на класи, соціально – економічні типи у відповідності з правилами наукового групування.

Приклад 1: Розподіл підприємств за формами власності.

№	Групи підприємств за формами власності	Кількість підприємств
		всього, од.	у % до підсумку
1	Державна власність	26 326	93,6%
2	Приватна власність	1 366	4,9%
3	Колективна власність	331	1,2%
4	Змішана власність	89	0,3%
	Всього	28 112	100%

Структурне групування - це розподіл однорідної сукупності на групи, що характеризують її структуру за якої-небудь ознакою.

Приклад 2: Групування по розміру доходу на душу населення.

№	Розмір грошового доходу, грн. у місяць	Чисельність населення
		всього, тис. чол.	в % до підсумку
1	До 100	2,4	1,6
2	100-170	23,4	15,8
3	170-240	34,8	23,5
4	240-310	29,4	19,8
5	310-380	20,7	13,9
6	380-450	13,5	9,1
7	450-520	8,7	5,9
8	520 і більше	15,5	10,4
	Всього	148,4	100

Аналітичне групування є групування яке виявляє взаємозв'язки між досліджуваними явищами та їх ознаками.

Ознаки групувань бувають:

• чинникові (факторні)

• результативні.

Чинникові є ознаки під впливом яких змінюються інші ознаки які і утворять групу результативних ознак. Аналітичне групування служить для дослідження взаємозв’язку між факторними та результативною ознаками.

Приклад 3: Розподіл банків на групи за сумами активів балансу та зв'язок з кількістю занятих.

№	Сума активів балансу, млн. Грн.	Кількість банків, од	У середньому на один банк
			Чисельність зайнятих, чол	Балансовий прибуток, млн.грн
1	До 20	19	184	22,5
2	20-30	8	313	31,6
3	30-40	7	374	36,0
4	40-50	9	468	69,2
5	50 і більше	7	516	205,6
	Всього	50	328,8	60,0

Якщо в основі групування лежить кількісна ознака, то виділення груп пов’язано із створенням інтервалів зміни ознаки. Якщо ознака описова, то кількість груп дорівнює кількості типів.

Інтервал - величина окремої групи. Кількість інтервалів дорівнює кількості груп. Інтервали бувають відкриті і закриті У відкритих виділена одна межа, верхня або нижня (наприклад, «До30» або «50 і більше»), у закритих – обидві (наприклад, «30-50»). Закриті можуть бути рівними і нерівними.

Якщо варіація значення ознаки значна, то використовуються нерівні інтервали, інакше - рівні

Якщо ознака дискретна, то верхня межа попереднього інтервалу відрізняється на 1 від нижньої межі наступного (наприклад, 30-49, 50-69, 70-89 і т.д.).

Якщо ознака безперервна, то нижня межа наступного інтервалу рівна верхній межі попереднього (наприклад, 30-50, 50-70, 70-90 і т.д.). У такому випадку, нижня межа формується включно, а верхня - виключно. Значить, значення ознаки рівне 50 потрапляє у другий інтервал, а не в перший.

Кількість інтервалів залежить від коливання ознак: чим більше коливання, тим більше інтервалів. Виділені інтервали повинні бути достатньо заповнені. Якщо є незаповнені інтервали, їх кількість треба зменшити. При малій кількості інтервалів можуть виявитися невиявлені властивості сукупності.

Число утворених груп можна встановити аналітично за формулою Стерджеса: ,

де N – число груп (інтервалів);

K – число одиниць сукупності

Число інтервалів, яке відповідає обсягу сукупності K і розраховано за формулою Стерджеса, наведено в таблиці:

Обсяг сукупності, K	15-24	25-44	45-89	90-179	180-359	360-719
Число інтервалів, N	5	6	7	8	9	10

Я кщо вирішене питання про число інтервалів, то довжина одного інтервалу визначається так:

де N - кількість інтервалів,

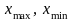- максимальне і мінімальне значення ознак, R - розмах.

Можна також здійснювати комбіноване групування на основі об’єднання різних видів групувань.

Додаткова література:

1. Теорія статистики, А.М.Єріна. – Київ, «Знання», 2001р., с. 26-36

2. Статистика: Навчальний посібник /Р.В.Фещур, А.Ф.Барківський, В.П. Кічор. 2-е вид. оновлене і доповнене. –Львів: «Інтелект-Захід», 2003р., с. 20-22

3. Теория статистики, под ред. Р.А.Шмойловой. – Москва, «Финансы и статистика», 1998р., с. 65-101