Классическая вероятностная модель

Простейшей математической моделью дискретного случайного эксперимента является так называемая <<классическая>> модель, в которой пространство элементарных исходов – конечное множество, и вероятности всех элементарных исходов равны. Если любые элементарные события равновероятны, то пространство элементарных событий называется симметричным.

Пусть число элементарных событий <<симметричного>> эксперимента конечно и равно , т.е. пространство элементарных событий . Обозначим вероятности элементарных исходов для любого . Тогда

и для любого получаем, что вероятность элементарного исхода равна .

Если имеется равновозможных элементарных исходов, то вероятность любого сложного события , состоящего из элементарных исходов, по определению вероятности события, равна

,

т.е. в рамках классической модели вероятности события она определяется как отношение числа элементарных исходов, благоприятных событию , к общему числу элементарных исходов:

.

Отсюда в частности, следует, что вероятность полного события , включающего все элементарных событий равна единице:

, т.е. - достоверное событие. Это определение – результат принятия гипотезы равновероятности элементарных событий.

Рассмотрим следующий пример. В случае с игральной костью при одном бросании равновозможно выпадение любой из шести граней, на которых нанесены цифры . Пространство элементарных событий

и вероятность любого равна . Пусть событие - выпадение чётного числа очков, т.е. появления одного из элементарных событий . Тогда .

Комбинаторика

Согласно классическому определению подсчёт вероятности события сводится к подсчёту числа благоприятствующих ему исходов.

Делают это обычно комбинаторными методами.

Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчёте числа комбинаций (выборок), получаемых из элементов заданного конечного множества. В каждой из них требуется подсчитать число возможных вариантов осуществления некоторого действия, ответить на вопрос <<сколькими способами?>>.

Многие комбинаторные задачи можно решить с помощью двух важных правил, называемых соответственно правилами сложения и умножения.

Правило умножения (основной принцип): если из некоторого конечного множества первый объект (элемент ) можно выбрать способами и после каждого такого выбора второй объект (элемент ) можно выбрать способами, то оба объекта ( и ) в указанном порядке можно выбрать способами.

Этот принцип распространяется на случай трёх и более объектов.

Пример 1. Сколько трёхзначных чисел можно составить из цифр , если: а) цифры не повторяются? б) цифры могут повторяться?

Подсчитаем число способов выбора цифры для первого места слева

в трёхзначном числе (эти места помечены звёздочками) . Коль скоро цифр 5 то очевидно, что на первое место в трёхзначном числе можно поставить любое из указанных чисел. Поэтому число способов выбора равно 5. После того как первое место занято, например, то осталось четыре цифры для заполнения второго места. После заполнения второго места, например, для заполнения третьего места остаётся выбор из трёх цифр. Например, . Поэтому согласно правилу умножения имеется способов расстановки цифр, т.е. искомое число трёхзначных чисел есть . Если цифры могут повторяться, то трёхзначных чисел будет .

Правило суммы. Если некоторый объект можно выбрать способами, а объект можно выбрать способами, причём первый и второй способы не пересекаются, то любой из указанных объектов ( или ), можно выбрать способами.

Это правило распространяется на любое конечное число объектов.

Пример 2. В студенческой группе девушек и юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

По правилу умножения двух девушек можно выбрать способами, а двух юношей - способами. Следует выбрать студентов одного пола: двух студенток или двух юношей. Согласно правилу сложения таких способов выбора будет .

Существуют две схемы выбора элементов из различных элементов рассматриваемого множества: без возвращения (без повторений) и с возвращением (с повторением). В первом случае выбранные элементы не возвращаются обратно; можно отобрать сразу все элементов или последовательно отбирать их по одному. Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.

Схема выбора без возвращений

Пусть дано множество, состоящее из различных элементов.

Размещением из элементов по элементов называется любое упорядоченное подмножество данного множества, содержащее элементов.

Из определения вытекает, что размещения – это выборки (комбинации), состоящие из элементов, которые отличаются друг от друга либо составом элементов, либо порядком их расположения.

Число размещений из элементов по элементов обозначается символом (<<A из эн по эм>>) и вычисляется по формуле

или

, где , , .

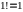Для составления размещения надо выбрать элементов из множества с элементами и упорядочить их, т.е. заполнить мест элементами множества. Первый элемент можно выбрать способами, т.е. на первое место можно поместить любой из элементов. После этого второй элемент можно выбрать из оставшихся элементов способами. Для выбора третьего элемента имеется способа, четвёртого - способа, и, наконец, для последнего - ого элемента - способов. Таким образом, по правилу умножения, существует способов выбора элементов из данных элементов, т.е. .

Пример 3. Составить различные размещения по из элементов множества ; подсчитать их число.

Из трёх элементов можно образовать следующие размещения по два элемента: , , , , , . Число размещений из трёх по два равно .

Перестановкой из элементов по элементов. Число перестановок по из элементов обозначается символом (<<пэ из эн>>) и вычисляется по формуле

.

Эта формула следует из определения перестановки:

.

Пример 4. Составить различные перестановки из элементов множества ; подсчитать их число.

Из элементов данного множества можно составить следующие перестановки: , , , , , . По формуле для расчёта перестановок имеем: .

Пример 5. Сколькими способами можно расставить на полке различных книг?

Искомое число способов равно числу перестановок из элементов (книг), т.е. .

Сочетанием из элементов по ( ) элементов называется любое подмножество, которое содержит элементов данного множества.

Из определения вытекает, что сочетания – это выборки (комбинации), каждая из которых состоит из элементов, взятых из данных элементов, и которые отличаются друг от друга хотя бы одним элементом, т.е. отличаются только составом элементов.

Число сочетаний из элементов по обозначается символом

(<<цэ из эн по эм>>) и вычисляется по формуле.

или

.

Число размещений из элементов по можно найти следующим образом: выбрать элементов из множества, содержащего элементов (это можно сделать способами); затем в каждом из полученных сочетаний (подмножеств) сделать все перестановки для упорядочения подмножеств (это можно сделать способами). Следовательно, по правилу умножения, можно записать: . Отсюда .

Запишем следующее очевидное выражение

По существу эта формула представляет собой выражение для числа перестановок из элементов. Эта формула записана справа налево. Из этой формулы следует, что . Из этого соотношения следует, что .

С учётом последнего соотношения запишем

Имеют место формулы:

Эта формула доказывается очень просто. В выражении следует положить .

.

.

, .

Формула выражает число всех подмножеств из элементов (оно равно . Числа являются коэффициентами в разложении бинома Ньютона:

.

Пример 5. Составить различные сочетания по 2 из элементов множества

; подсчитать их число.

Из трёх элементов можно образовать следующие сочетания по два элемента: . Их число .

Пример 6. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? А если выбрать 1 красную гвоздику и розовых?

Так как порядок выбора цветов не имеет значения, то выбрать 3 цветка из вазы, в которой 14 гвоздик, можно способами. .

Далее: красную гвоздику можно выбрать способами. Выбрать две розовые гвоздики из имеющихся четырёх можно

способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить, по правилу умножения,

способами.

Схема выбора с возвращениями

Если при выборке из элементов из элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями.

Размещения с повторениями могут отличаться друг от друга элементами, их порядком и количеством повторений элементов. Число всех размещений из элементов по с повторениями обозначается символом и вычисляется по формуле

.

Отметим следующее, в схеме выбора без возвращений размещение такое, что . В схеме выбора с возвращением такого ограничения нет!

Пример 7. Из 3 элементов составить все размещения по два элемента с повторениями.

Число размещений с повторениями . Приведём эти способы размещений с повторениями: .

Пример 8. Сколько пятизначных чисел можно составить, используя цифры: а) 2, 5, 7, 8; б) 0, 1, 9?

а) Все пятизначные числа, составленные из цифр 2, 5, 7, 8, отличаются друг от друга либо порядком их следования (например, 25558 и 52855), либо самими цифрами (например, 52788 и 78888). Следовательно, они являются размещениями из 4 элементов по 5 с повторениями, т.е. . Таким образом, искомое число пятизначных чисел равно . Этот же результат можно получить, используя правило умножения: первую цифру в пятизначном числе можно выбрать четырьмя способами, вторую - тоже четырьмя способами, третью – четырьмя, четвёртую – четырьмя, пятую – четырьмя. Всего получается пятизначных чисел.

б) Если пятизначные числа состоят из цифр 0, 1, 9, то первую цифру слева можно выбрать двумя способами ( не может занимать первую позицию), каждую из оставшихся четырёх цифр можно выбрать тремя способами. Согласно правилу умножения, таких чисел будет .

(Иначе .).

Если при выборке элементов из элементы возвращаются обратно без последующего упорядочения, то говорят, что это сочетания с повторениями.

Число сочетаний из элементов по с повторениями обозначается символом и вычисляется по формуле

.

Напомним, что в схеме выбора без возвращений величина такая, что . В схеме выбора с повторениями должно быть или . Другими словами в этой схеме возможно неравенство .

Пример 9. Из трёх элементов составить все сочетания по два элемента с повторениями.

Это число сочетаний по два с повторениями равно . Составляем эти сочетания с повторениями: .

Пример 10. Сколькими способами можно составить букет из 5 цветов, если в наличии есть цветы трёх сортов?

Рассматриваемое множество состоит из трёх различных элементов, а выборки имеют объём, равный 5. Поскольку порядок расположения цветов в букете не играет роли, то искомое число букетов равно числу сочетаний с повторениями из трёх элементов по 5 в каждом. Поэтому число букетов можно подсчитать по формуле

.

Пусть в множестве с элементами есть различных элементов, при этом 1-ый элемент может повторяться раз, 2-ой элемент - раз …, -й элемент - раз, причём .

Перестановки из элементов данного множества называют перестановками с повторениями из элементов.

Число перестановок с повторениями из элементов обозначается символом и вычисляется по формуле

.

Пример 11. Сколько различных пятизначных чисел можно составить из цифр 3,3,5,5,8?

Заметим, что , , . Далее .

Число чисел можно рассчитать по формуле

.