2. Проведём теперь доказательство справа налево .

Пусть . Тогда, по определению операции пересечения, можно записать, что и .

Рассмотрим два случая.

а) Предположим, что . Тогда очевидно, что . Следовательно, и мы имеем в этом случае .

б) Предположим, что . В этом случае из выражения для заключаем, что элемент является общим для множеств и , то есть . Но тогда , таким образом и в этом случае .

Так как мы доказали, что и , то это может быть только тогда, когда .

Теория вероятностей – это наука о закономерностях случайных событий. Под событием в теории вероятностей понимается всякий факт, который может произойти или не произойти при осуществлении определённого комплекса условий. Каждое такое осуществление называется испытанием, опытом или экспериментом.

События можно подразделить на следующие три вида: - достоверные,

- невозможные и - случайные.

Достоверным называется событие, которое обязательно произойдёт при испытании.

Невозможным называется событие, которое заведомо не произойдёт при испытании.

Случайным называется событие, которое в результате эксперимента может либо произойти, либо не произойти.

Предметом теории вероятностей являются вероятностные закономерности массовых случайных событий, где под массовостью событий понимается многократная их повторяемость.

Рассмотрим примеры событий:

1) - появление герба при бросании монеты;

2) - появление трёх гербов при трёхкратном бросании монеты;

3) - попадание в цель при выстреле.

Как видим, каждое из этих событий обладает какой-то степенью возможности. Для того чтобы количественно сравнивать между собой события по степени их возможности, нужно с каждым событием связать определенное число.

Вероятность события есть численная мера степени объективной возможности этого события. В качестве единицы измерения вероятности принята вероятность достоверного события. Вероятность невозможного события равна нулю, а вероятность любого случайного события обозначается и изменяется в диапазоне от нуля до единицы: . В рамках рассматриваемой теории случайные события должны удовлетворять трем основным предположениям.

Первое предположение состоит в том, что случайные величины являются результатами действия многих разнообразных причин, присущих реальному комплексу условий, которые не поддаются строгому учету и контролю, оказывают «мешающее» влияние на окончательный исход эксперимента, придают ему стохастический (случайный) характер. Именно это влияние не позволяет точно предвидеть, произойдет или нет интересующее нас событие.

Второе предположение состоит в том, что мы имеем принципиальную возможность многократного (в принципе, неограниченного) осуществления наблюдений при повторении рассматриваемого эксперимента в неизменных рамках действия одного и того же комплекса условий.

Третьим требованием, которым обычно ограничивается класс рассматриваемых в теории вероятностей случайных экспериментов и соответствующих им случайных событий и которое оправдывает идею приписывания случайному событию вероятности как численной меры возможности его осуществления, является требование выполнения свойства устойчивости частот. Оно заключается в следующем.

Проведем серию из испытаний ( назовем длиной серии), в каждом из которых может произойти или не произойти событие , и подсчитаем, сколько раз в этой серии эксперимент заканчивался наступлением события Обозначив это число через и разделив его на общее число всех повторений эксперимента (длину серии наблюдений) , получим величину , называемую относительной частотой наступления события в серии из повторений эксперимента (в дальнейшем будем называть это число просто частотой события ).

Пусть можно повторить этот эксперимент при неизменном реальном комплексе условий любое количество раз. При небольшом числе экспериментов частота носит случайный характер и может заметно меняться от одной группы опытов к другой. При увеличении числа экспериментов случайные обстоятельства, свойственные каждому отдельному эксперименту, в массе взаимно погашаются, и частота проявляет тенденцию к стабилизации, приближаясь к некоторой средней величине .

Этот эмпирический факт, наблюдаемый при конечном числе экспериментов, и положен в основу теории вероятностей.

В качестве примеров укажем на опыт Бюффона, в котором симметричная монета подбрасывалась 4040 раз, а герб выпадал раз (частота появления герба в данной серии наблюдений равна, , что близко к интуитивно ожидаемому значению вероятности 0,5). Аналогично в опыте Пирсона с монетой было произведено , опытов и получено выпадений герба соответственно 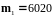, , и соответственно частоты равны , . Это объективно существующее число и называется вероятностью события.

Частота события отличается от вероятности этого события тем, что вероятность — величина детерминированная, а частота — величина случайная, до опыта не известная.

Из теоремы Бернулли вытекает принцип практической невозможности маловероятных событий: если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это событие не наступит. Достаточно малую вероятность, при которой событие можно считать практически невозможным, называют уровнем значимости.

Вероятностное пространство

Случайные события и операции над ними

Для того чтобы формально описать некоторый эксперимент, т.е. создать математическую модель некоторой экономической ситуации, нужно указать все возможные варианты исхода, которыми может за­кончиться эксперимент. Считается, что в результате эксперимента должен произойти только один из этих возможных исходов.

Определение. Совокупность всех возможных исходов эксперимента называют пространством элементарных событий данного эксперимента и обозначают , а каждый исход называется элементарным событием.

Если все эти исходы можно перечислить: или , то такое пространство называется дискретным (конечным или счетным).

Рассмотрим несколько примеров экспериментов и соответствующих им пространств элементарных событий.

1. Подбрасывание монеты: ( - выпадение герба, - вы­падение решки).

2. Выбрасывание одной игральной кости:

.

3.Четырёхкратное бросание игральной кости:

.

4.Проверка (по альтернативному признаку) одного изделия, случайно отобранного из продукции массового производства: .

5.Проверка (по альтернативному признаку) изделий, случайно отобранных из продукции массового производства: , где — число обнаруженных дефектных деталей.

6.Проверка (по альтернативному признаку) двух выборок, состоящих соответственно из , и , изделий, случайно отобранных из продукции массового производства:

.

Кроме элементарных событий, рассматриваются так называемые сложные события.

Например, события — выпадение четного числа очков, — выпавшее число очков не превзойдет трех — запишутся соответственно, и .

Определение. В случае конечного или счетного пространства элементарных событий событием называется любое подмножество пространства элементарных событий .

Осуществление любого из элементарных событий, входящих в , влечет за собой осуществление события : говорят, что событие произошло, если эксперимент закончился элементарным исходом .

Введем некоторые соотношения между событиями.

Если при каждом осуществлении эксперимента, при котором происходит событие происходит также и событие , то говорят, что событие влечет за собой событие , и это обстоятельство обозначается , т.е. событие принадлежит событию .

Если событие влечет за собой событие и в то же время событие влечет за собой событие , то говорят, что события и равносильны: .

Объединением (суммой) событий и называется событие , которое происходит тогда, когда наступает хотя бы одно из событий или .

Пересечением (произведением), событий и называется событие, которое наступает тогда, когда происходят и событие , и событие одновременно.