Операции над множествами
На множествах определяют некоторые теоретико-множественные операции. Результат таких операций – новое множество.
Рассмотрим наиболее важные из этих операций.
Объединением множеств и называют множество , состоящее из элементов принадлежащих множествам или , что обозначается:
.
Таким образом, множество можно задать следующим образом:
.
Результат операции объединения представим диаграммой Эйлера-Вьенна.
Результат объединения множеств
Результат операции объединения множеств и представлен на рисунке в виде заштрихованной области.
Пересечением множеств и называют множество , состоящее из элементов, которые являются общими для множеств и .
Обозначают так:
.
Множество можно задать следующим образом:
.
Р езультат операции пересечения множеств и можно представить на диаграмме Эйлера-Вьенна как общую часть областей, изображающих эти множества.
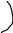
Результат пересечения множеств
Эта область на рисунке заштрихована.
Разностью множеств и называют множество , состоящее из таких элементов множества , которые не являются элементами множества .
Обозначают так:
.
Множество можно задать также следующим образом:
.
Результат разности множеств .
Результат разности множеств и представлен на диаграмме Эйлера-Вьенна как часть множества , которая не имеет общих элементов с множеством .
Дополнением
множества
называют множество
,
которое является разностью универсального
множества
и множества
,
то есть
.
Множество можно задать следующим образом:
.
Дополнение множества
Дополнение множества представлено на диаграмме Эйлера-Венна как часть множества , которая не имеет общих элементов с множеством . область на рисунке заштрихована.
Свойства операций над множествами
Чтобы записывать и преобразовывать теоретико-множественные выражения, необходимо знать свойства операций над множествами.
Основные из этих свойств следующие:
1. Коммутативность:
;
;
2.Ассоциативность:
;
;
3.Дистрибутивность:
;
;
4. Законы де Моргана:
;
.
5. Идемпотентность:
;
.
6. Законы поглощения:
;
.
7. Закон двойного дополнения:
.
8. Операции с универсальным и пустым множествами:
;
;
;
;
;
.
Если внимательно рассмотреть свойства теоретико-множественных операций, то можно сформулировать правило, известное как принцип двойственности.
Теоретико-множественное выражение, содержащее операции объединения
,
пересечения
, дополнения
, а также универсальное множество
и пустое множество , останется справедливым, если в нём произвести следующие замены:
;
;
;
;
.
Все перечисленные выше свойства можно доказать по одной схеме.
Пусть
требуется доказать теоретико-множественное
равенство
,
где
и
есть некоторые множества.
Первая
часть доказательства состоит в том,
чтобы показать, что если некоторый
элемент принадлежит множеству
,
то он также принадлежит множеству
.
Этим доказывается справедливость
соотношения
.
Вторая
часть доказательства состоит в
необходимости показать, что если
некоторый элемент принадлежит множеству
,
то он также принадлежит множеству
.
Этим доказывается справедливость
соотношения
.
Тогда из соотношений и следует вывод, что .
Пример. Пусть требуется доказать, что
.
Очевидно,
что здесь
и
.
1.
Проводим доказательство <<слева
направо>>
.
Пусть
имеется элемент
такой, что
.
Тогда из определения операции объединения
следует, что этот элемент принадлежит
множеству
(
)
или множеству
(
).
Рассмотрим каждый из этих случаев.
a) Если , то по определению операции объединения, имеем:
и
.
Следовательно, этот элемент будет общим
для этих множеств, то есть
.
Для данного случая доказано
.
б)
Если
,
то элемент
является общим для каждого из множеств
и
,
то есть
и
.
Но тогда будем иметь, что
и
.
Следовательно,
принадлежит и пересечению множеств
и
.
Другими словами, и для данного случая
.