1) Посещение узла n 2) Прохождение левого поддерева 3) Прохождение правого поддерева

Симметричный метод 1) начинает свои действия в узле спуском по его левому поддереву, 2) затем выполняется второе действие обработки данных в узле 3) далее рекурсивное прохождение правого поддерева.

При обратном прохождении посещение узла откладывается до тех пор, пока не будут рекурсивно пройдены оба его поддерева: 1) Рекурсивное прохождение левого поддерева 2) Рекурсивное прохождение правого поддерева 3) прохождение узлов.

В каждом рассмотренном случае, сначала осуществлялось прохождение по левому поддереву, а уже потом по правому. Фактически существует еще три алгоритма, которые выбирают сначала правое поддерево, а потом левое.

Пример.

Рисунок…

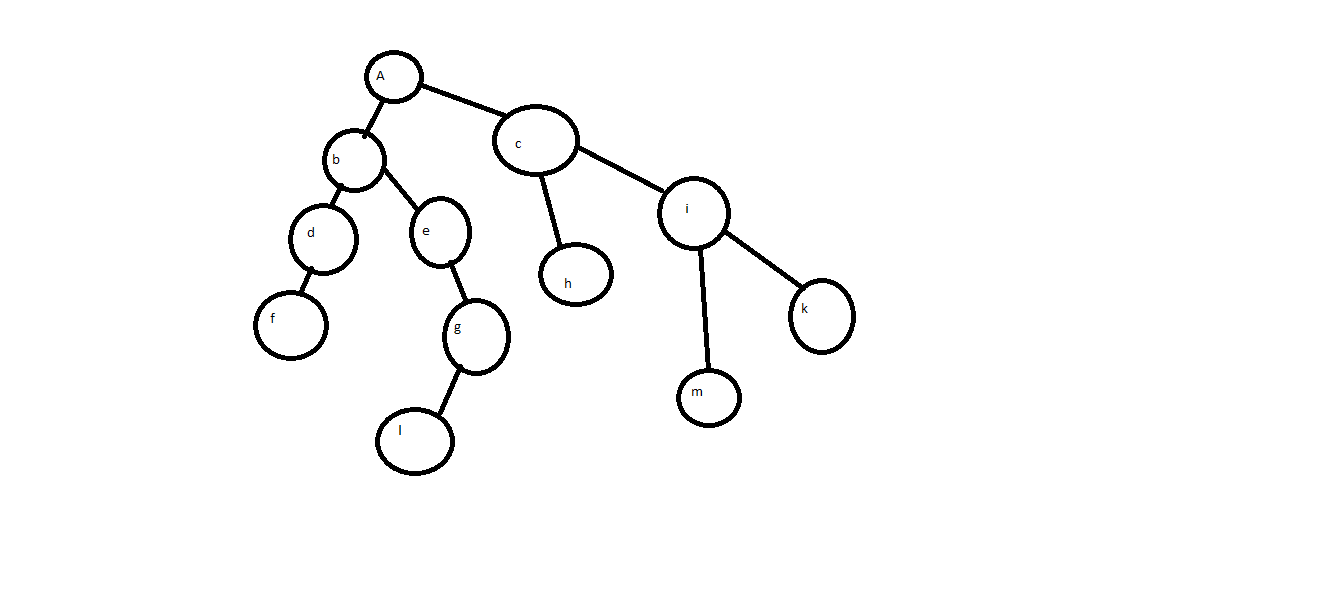
Прямой A B D F E G L ^L C H I M K ^R

Симметричное F D B E L G ^L A M C M I K ^R

Обратное F D L G E B ^L H M K I C A ^R

Бинарные деревья.

Идеально сбалансированное дерево. n элементов. Пусть у нас дано n элементов, из которых нужно построит дерево минимальной глубины. Минимальная высота при заданном числе вершин достигается, если на всех уровнях кроме последнего помещается максимально - возможное число вершин. Этого легко добиться, размещая приходящие вершины поровну слева и справа от каждой вершины. Дерево называется идеально сбалансированным, если число вершин в его левых и правых поддеревьях отличается не более чем на единицу. Алгоритм построения идеального дерева состоит из трех шагов: 1) Взять одну вершину в качестве корня. 2) Тем же способом построить левое поддерево с количеством вершин nl=nDIV2. 3) Тем же способом построить правое поддерево nr=n-nl-1. Заполнение идеально сбалансированного дерева осуществляется согласно прямого метода прохождения, т.е. элементы заносятся в следующем порядке: первый элемент становится корнем, затем для каждой вершины поддерева уровня H вначале заполняется его левое поддерево, а затем правое.

Void Insert (int key, **T)

{ Node *new node;

If (T==0)

{

Newnode= new

Newnode->data=key;

Newnode->left= NULL;

newnode->right=NULL;

*T=new;

}

}

Tree *tree (int n, int *k)

{

Node *newnode;

Int nl, nr;

If (n==0)

newnode=0;

else

{

nj=n/2; nr=n-nl-1;

newnode=new;

newnode->data=k[i++];

newnode->left=tree (nl, *k);

newnode->right=tree (nr, *k);

}

Return newnode;

}

Пусть надо построить идеально сбалансированное дерево, содержащее n=11 количество вершин

17 1 4 7 13 84 3 15 52 45 46.

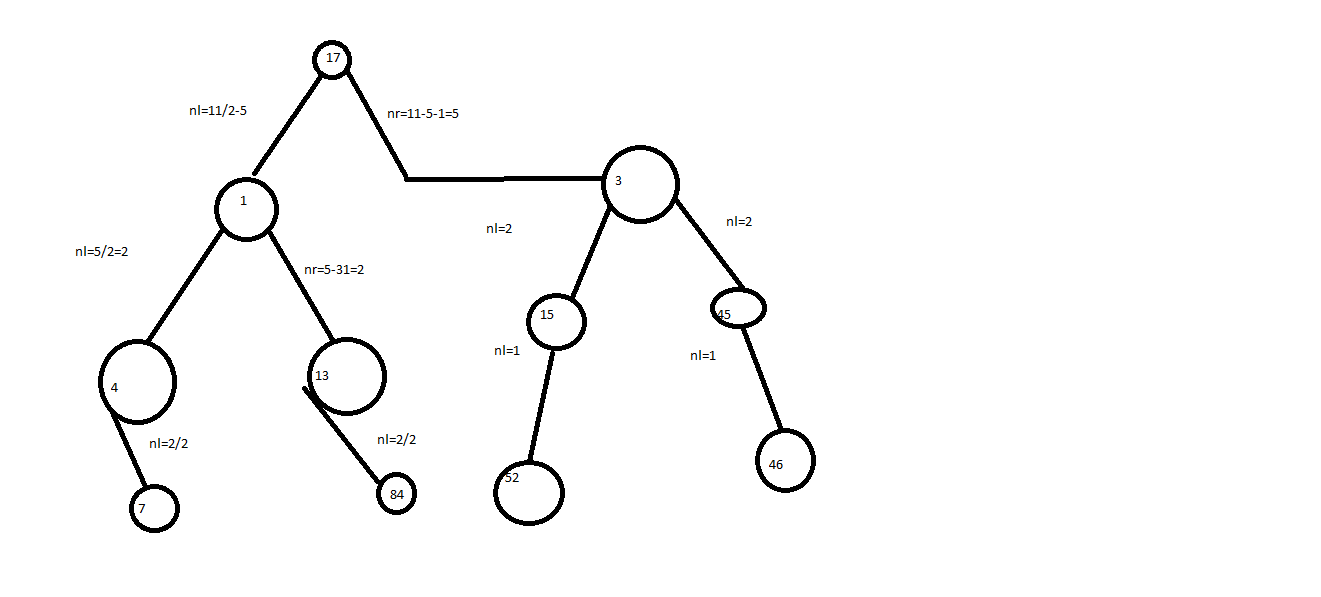
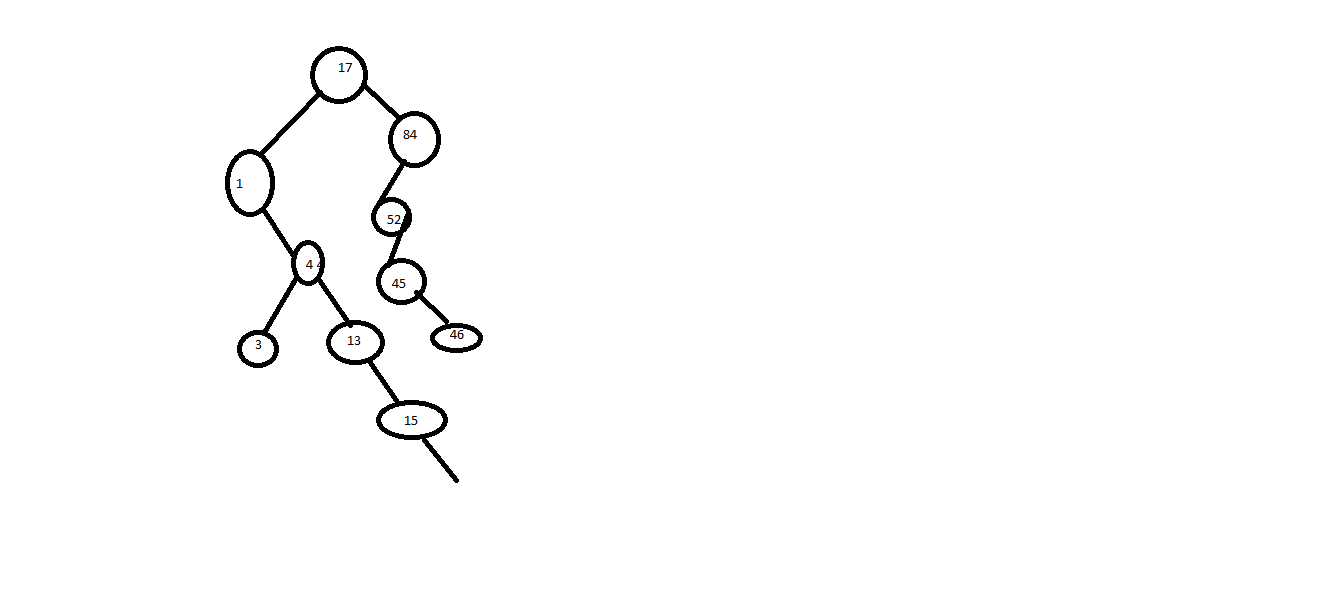
Бинарное дерево поиска.

Структура дерева, которая позволяет обеспечить эффективный доступ к элементам. Эта структура, называемая бинарным деревом поиска, упорядочивает элементы по средствам оператора отношения, чтобы сравнить узлы дерева, мы подразумеваем, что часть или все поле данных определено в качестве ключа, и оператор сравнивает ключи, когда размещает элемент на дереве. Бинарное дерево поиска строится по следующему правилу: для каждого узла значение данные в левом поддереве меньше чем в этом узле, а в правом дереве больше или равны.

Сбалансированно-поисковая. AVL– tree.

Рассмотрим модифицированный класс деревьев, обладающих всеми преимуществами бинарных деревьев поиска и никогда не вырождающихся.

Определение. Дерево называется сбалансированным тогда и только тогда, когда высоты двух поддеревьев каждой из его вершин отличаются не более чем на единицу.

AVL дерево представляет собой списковую структуру, похожую на бинарное дерево поиска с одним дополнительным условием: дерево должно оставаться сбалансированным по высоте после каждой операции включение или удаление. Для постоянного отслеживания соотношения высот левого и правого поддеревьев вводят показатель сбалансированности (баланс), который содержит разность высот левого и правого поддеревьев. Если баланс<0 узел перевешивает влево. Если показатель сбалансированности больше нуля, узел перевешивает вправо. Если показатель сбалансированности =0, то высота левого и правого поддерева равны, т.е. в AVL дереве показатель сбалансированности может принимать значения {-1,0,1}.

Процесс включения вершины состоит из следующих трех, последовательно выполняемых частей: 1. прохождение по пути поиска, пока не убедимся, что ключа в дереве нет. 2. Включение новой вершины и определение показателей сбалансированности, т.е. отступление по пути поиска и проверка в каждой вершине показателя сбалансированности. 3. Если необходимо, то проведение балансировки.

Балансировка.

Операция по балансировке состоит из последовательных переприсваиваний ссылок. Фактически, ссылки циклически м5няются местами, что приводит к одно-, или двукратному повороту двух и трех участвующих в процессе вершин. Кроме вращения ссылок нужно должным образом поправить показатель сбалансированности соответствующих вершин.

Повороты необходимы в том случае, когда родительский узел P становится разбалансированным.

Одинарный LL поворот происходит, когда Родительский узел P его левый L начинает перевешивать влево после включения узла в позицию X.

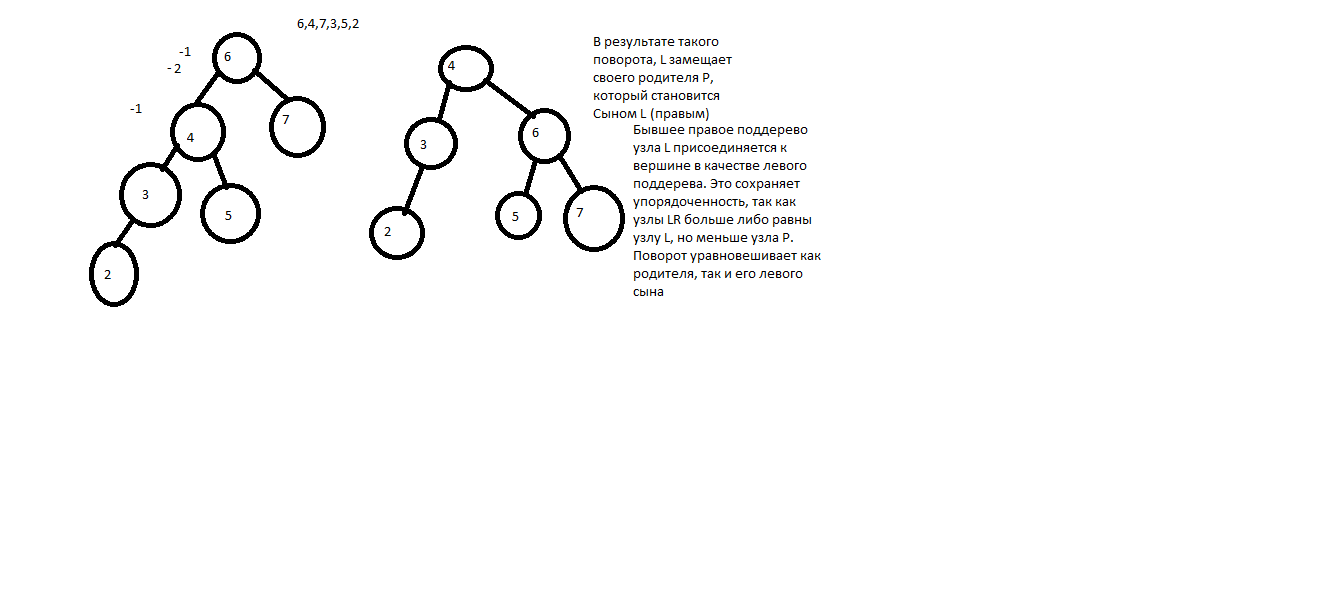
Однократный RR поворот возникает, когда родительский узел P и его правый сын R начинают перевешивать вправо после включения узла в позицию X.

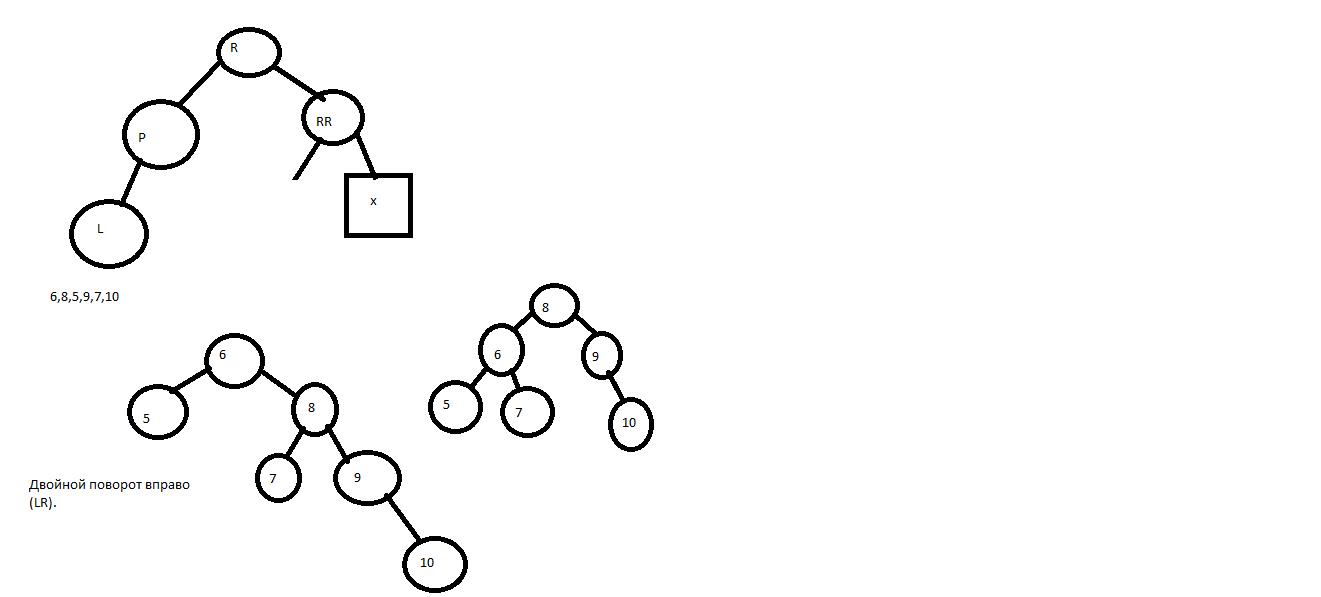
В

R

R

LR

L

X

LL

озникает, когда двойной узел P становится перевешивающим влево, а его левый сын L перевешивающим вправо. В результате поворота, узел LR замещает своего родителя P, а бывший родитель P становится правым сыном LR.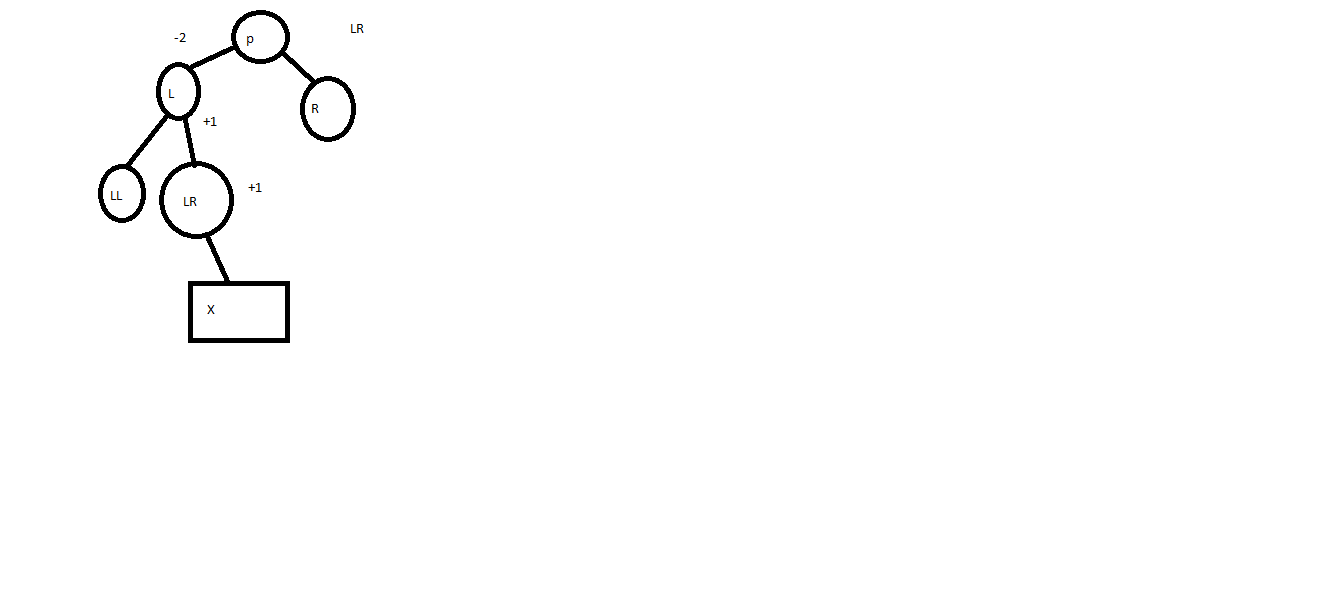

Двойной поворот влево или двойной RL поворот возникает в том случае, когда родительский узел P перевешивает вправо после включения узла в позицию X.

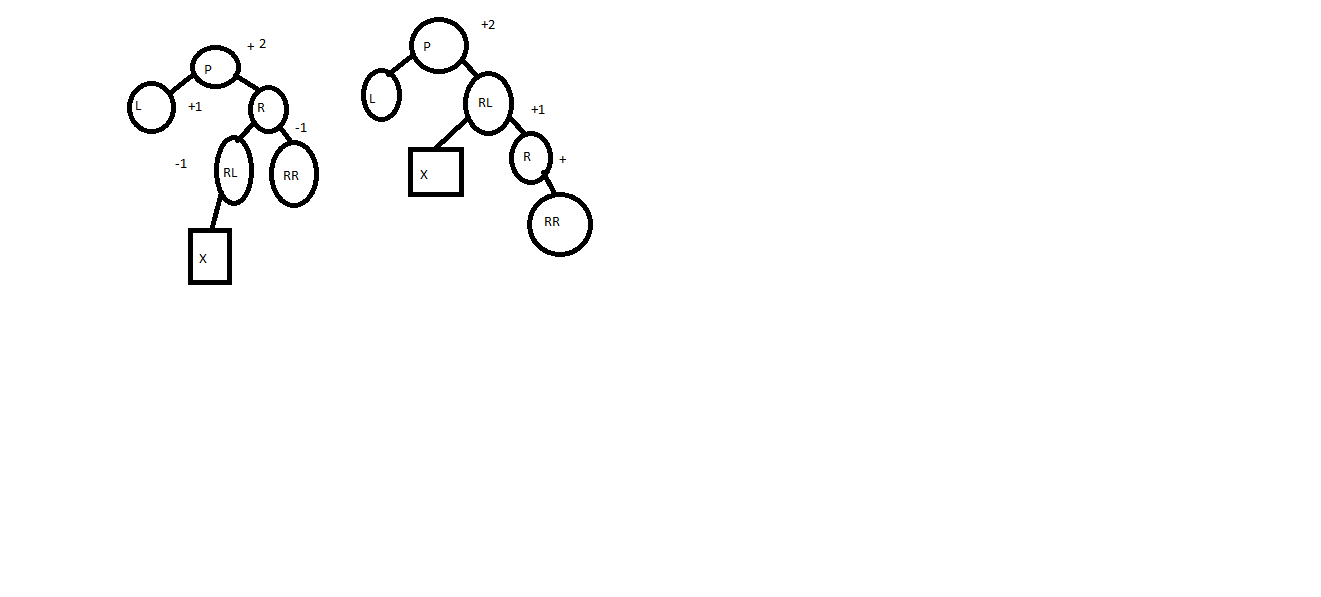
Удаление и исключение из сбалансированного дерева.

При удалении из AVL дерева возможно три варианта: 1. Исключаемый элемент является листом, т.е. не имеет потомков. В этом случае удаляется ссылка на этот элемент и проверяется, не нарушился ли баланс. Если необходимо, проводится балансировка. 2. Исключаемый элемент – терминальная вершина, т.е. имеет одного потомка. В этом случае исключаемый элемент заменяется на своего единственного потомка и проверяется, не нарушился ли баланс. Если необходимо, опять балансировка. 3. Удаляемый элемент- вершина с двумя потомками. В этом случае исключаемый элемент заменяется, либо на самый правый элемент левого поддерева (на самый большой в левом), либо на самый левый в правом. Балансировка (в то время, как включение одного узла может привести к одному повороту, исключение может потребовать поворота во всех вершинах вдоль пути поиска).

Д/З