2) Метод параметрической оптимизации линейного закона управления
Метод параметрической оптимизации линейного закона управления заключается в поиске таких значений параметров линейного закона управления, которые обеспечивают перевод объекта управления в заданное состояние за минимальное время и последующее удержание объекта в этом состоянии.
Одним из достоинств этого метода является возможность включения в закон управления только тех переменных состояния, которые соответствуют достаточно точно измеряемым физическим величинам. В случае водоизмещающего судна наиболее точно из принятых в рассмотрение физических величин измеряются угол рыскания и угловая скорость рыскания.
Поскольку в рассматриваемом случае изменение состояния судна вблизи целевой точки носит экспоненциальный характер, то теоретически время перехода в целевое состояние не ограничено. В связи с этим предлагается принимать за момент окончания процесса управления момент входа изображающей точки в область, точки которой откланяются от целевого состояния не более чем на 10% от начальной величины рассогласования.
Алгоритм программы поиска параметров линейного закона управления
Выбор параметров закона управления
Нахождение времени переходного процесса
Время минимально?
нет
Вывод графиков
Конец
да
Текст программы поиска параметров линейного закона управления
Текст основной программы:
V0=5.65; % скорость хода судна
L=51; % длина по ватерлинии
% коэффициенты математической модели судна
r21=-0.59;
r31=5.32;
q21=0.94;
q31=-2.41;
s21=-0.29;
s31=-3.4;
fi=V0/L; % нормирующая частота
a11=-r31*fi;
a12=-q31*fi^2;
a21=-r21;
a22=-q21*fi;
b11=-s31*fi^2;
b21=-s21*fi;
dt=0.007; % шаг для метода Эйлера
y1i=0;
y2i=0; %данные для метода Эйлера
y3i=10*3.14/180;
T2=0;
Y2=[y1i,y2i,y3i];
k0=[-1;-2]; % начальные точки для коэффициентов обратных связей
k=fminsearch('myfun3',k0);
k
ug=-k(1)*y1i-k(2)*y3i; % управления при вводе коэффициентов обратных связей
if(abs(ug)>35*3.14/180)
ug=sign(ug)*35*3.14/180; % управление
end
for t=dt:dt:40
u=-k(1)*y1i-k(2)*y3i;
if(abs(u)>35*3.14/180)
u=sign(u)*35*3.14/180;
end
y1j=y1i+dt*(a11*y1i+a12*y2i+b11*u);
y2j=y2i+dt*(a21*y1i+a22*y2i+b21*u);
y3j=y3i+dt*(y1i);
T2=[T2;t];
Y2=[Y2;y1j y2j y3j];
ug=[ug;u];
y1i=y1j;
y2i=y2j;
y3i=y3j;
end
m=0;
tk=1000;
i=length(T2);
while(m<0.01)
m=max([abs(Y2(i,1)),abs(Y2(i,2)),abs(Y2(i,3))]);
i=i-1;
end
tk=T2(i+1);
figure(1)
plot(T2,Y2(:,1),T2,Y2(:,2),T2,Y2(:,3),T2,ug,'m')
legend('x1','x2','x3','u');
xlabel('t,c');
grid on;
Текст функции myfun3:
function a=myfun3(k) %подбираем вектор k при котором а будет минимальным
V0=5.65; % скорость хода судна
L=51; % длина по ватерлинии
% коэффициенты математической модели судна
r21=-0.59;
r31=5.32;
q21=0.94;
q31=-2.41;
s21=-0.29;
s31=-3.4;
fi=V0/L; % нормирующая частота
a11=-r31*fi;
a12=-q31*fi^2;
a21=-r21;
a22=-q21*fi;
b11=-s31*fi^2;
b21=-s21*fi;
dt=0.007; % шаг для метода Эйлера
y1i=0;
y2i=0;
y3i=10*3.14/180;
T2=0;
Y2=[y1i,y2i,y3i];
ug=-k(1)*y1i-k(2)*y3i;
if(abs(ug)>35*3.14/180)
ug=sign(ug)*35*3.14/180;
end
for t=dt:dt:25
u=-k(1)*y1i-k(2)*y3i;
if(abs(u)>35*3.14/180)
u=sign(u)*35*3.14/180;
end
y1j=y1i+dt*(a11*y1i+a12*y2i+b11*u);
y2j=y2i+dt*(a21*y1i+a22*y2i+b21*u);
y3j=y3i+dt*(y1i);
T2=[T2;t];
Y2=[Y2;y1j y2j y3j];
ug=[ug;u];
y1i=y1j;
y2i=y2j;
y3i=y3j;
end
m=0; % отклонение от установившегося значения
tk=1000; ; % время по истечении которого входит в коридор (можно взять 0)
% находим конец ПП
i=length(T2);
while(m<0.01)
m=max([abs(Y2(i,1)),abs(Y2(i,2)),abs(Y2(i,3))]);
i=i-1;
end
tk=T2(i+1);
a=((Y2(length(T2),1))^2+(Y2(length(T2),2))^2+(Y2(length(T2),3))^2+tk);
% минимизация а для нахождения коэффициентов обратных связей
Результаты работы программы:
Найденные значения параметров линейного закона управления:
k1 =-5,5525, k2 = 4,32.
Время переходного процесса составило15,25 с, что несколько больше чем при использовании метода, основанного на теореме об N интервалах.
Графики переходных процессов:
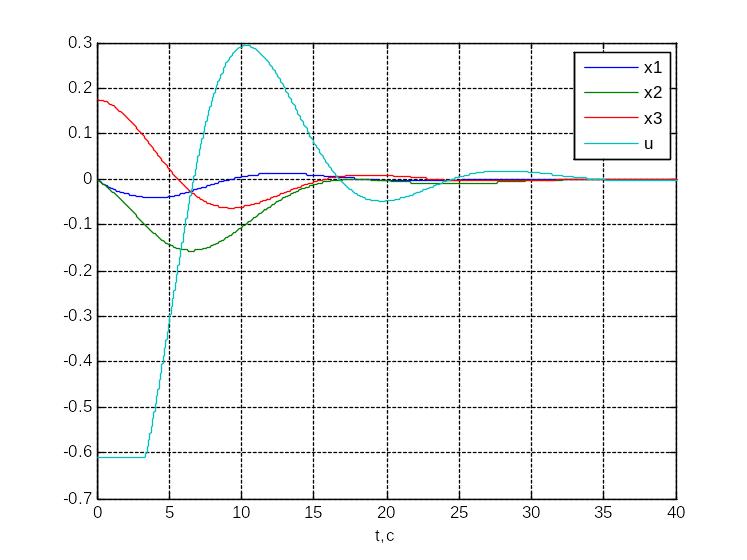
Рис. 3. Переходные процессы в системе.
x1 – (угловая скорость рыскания);
x2 – (угол дрейфа);
x3 – φ (угол рыскания);
u – (угол перекладки руля).